一、递归遍历方法： 

先序遍历：

Status PreOrderTraverse(Tree *t) {if (t == NULL) return OK;//合法性检查else {visit(t->data);//访问根节点PreOrderTraverse(t->lchild);//递归遍历左子树PreOrderTraverse(t->rchild);//递归遍历右子树}
}

 

中序遍历

Status InOrderTraverse(Tree *t) {if (t == NULL) return OK;//合法性检查else {PreOrderTraverse(t->lchild);//递归遍历左子树visit(t->data);//访问根节点PreOrderTraverse(t->rchild);//递归遍历右子树}
}

 后序遍历

Status PostOrderTraverse(Tree *t) {if (t == NULL) return OK;//合法性检查else {PreOrderTraverse(t->lchild);//递归遍历左子树PreOrderTraverse(t->rchild);//递归遍历右子树visit(t->data);//访问根节点}
}

 三种遍历算法的分析：

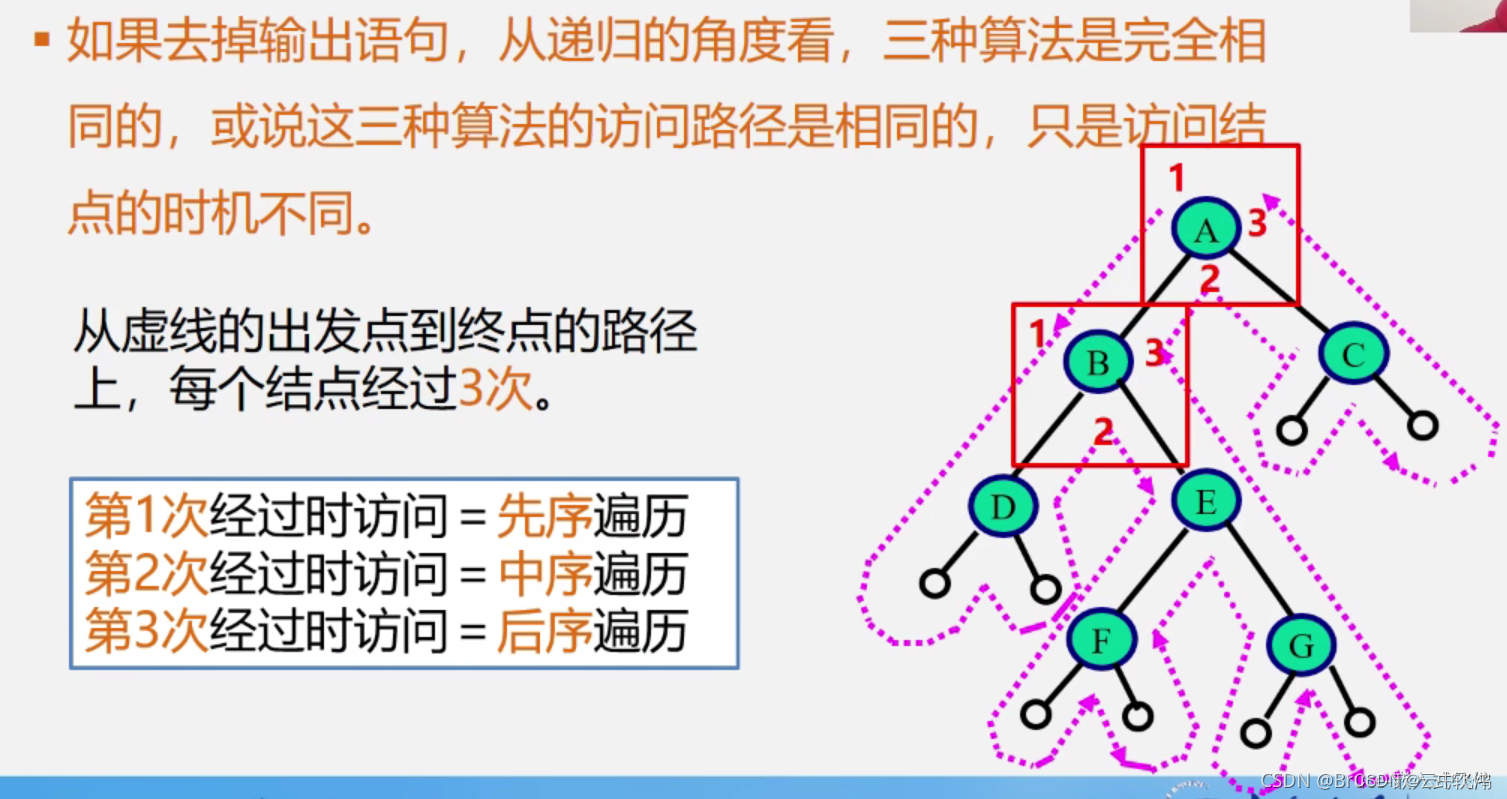
 二、非递归遍历算法：

Status PreOrderTraverse(Tree *t){Tree p=t;InitStack(s);//初始化while(p||!StackEmpty(s)){if(p){Push(s,p);printf("%c",q->data);p=p->lchild;//入栈}else{Pop(s,q);//出栈p=q->rchild;}}return OK;
}
Status InOrderTraverse(Tree *t){Tree p=t;InitStack(s);//初始化while(p||!StackEmpty(s)){if(p){Push(s,p);p=p->lchild;//入栈}else{Pop(s,q);printf("%c",q->data);//出栈p=q->rchild;}}return OK;
}

三、 层次遍历算法

void LevelOrder(TreeNode* t) {TreeNode* p; Queue *q;InitQueue(q);//初始化队列；InQueue(q,t);//根结点入队；while(!QueueEmpty(q)){DeQueue(q,p);//出队放入p中printf("%c",p->data);//访问p结点；if(p->lchild) InQueue(q,p->lchild);//左孩子不为空则入队；if(p->rchild) InQueue(q,p->rchild);//右孩子不为空则入队；}
}

                        
原文链接：https://blog.csdn.net/weixin_46432495/article/details/120497774