---

---

计算图

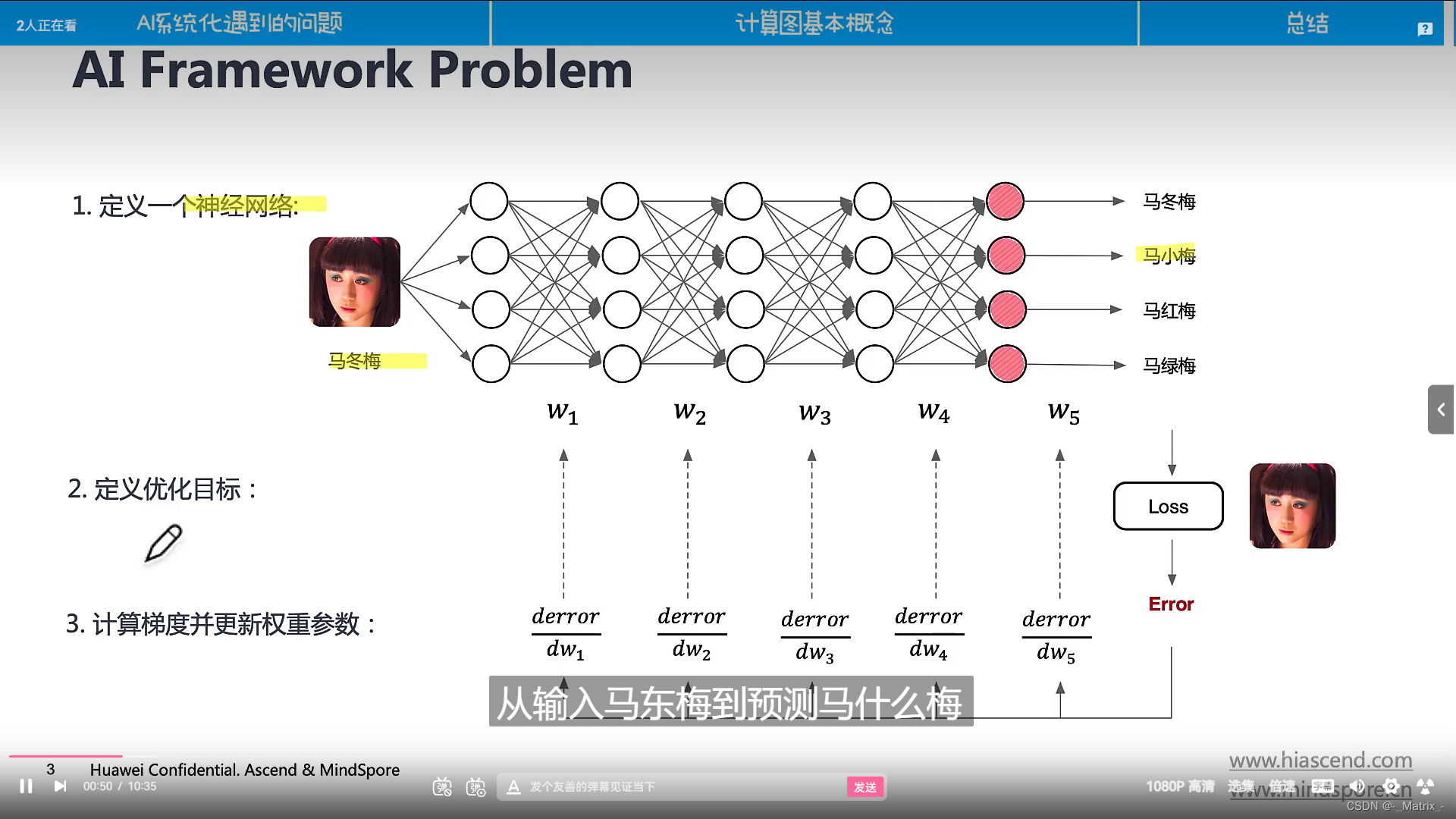
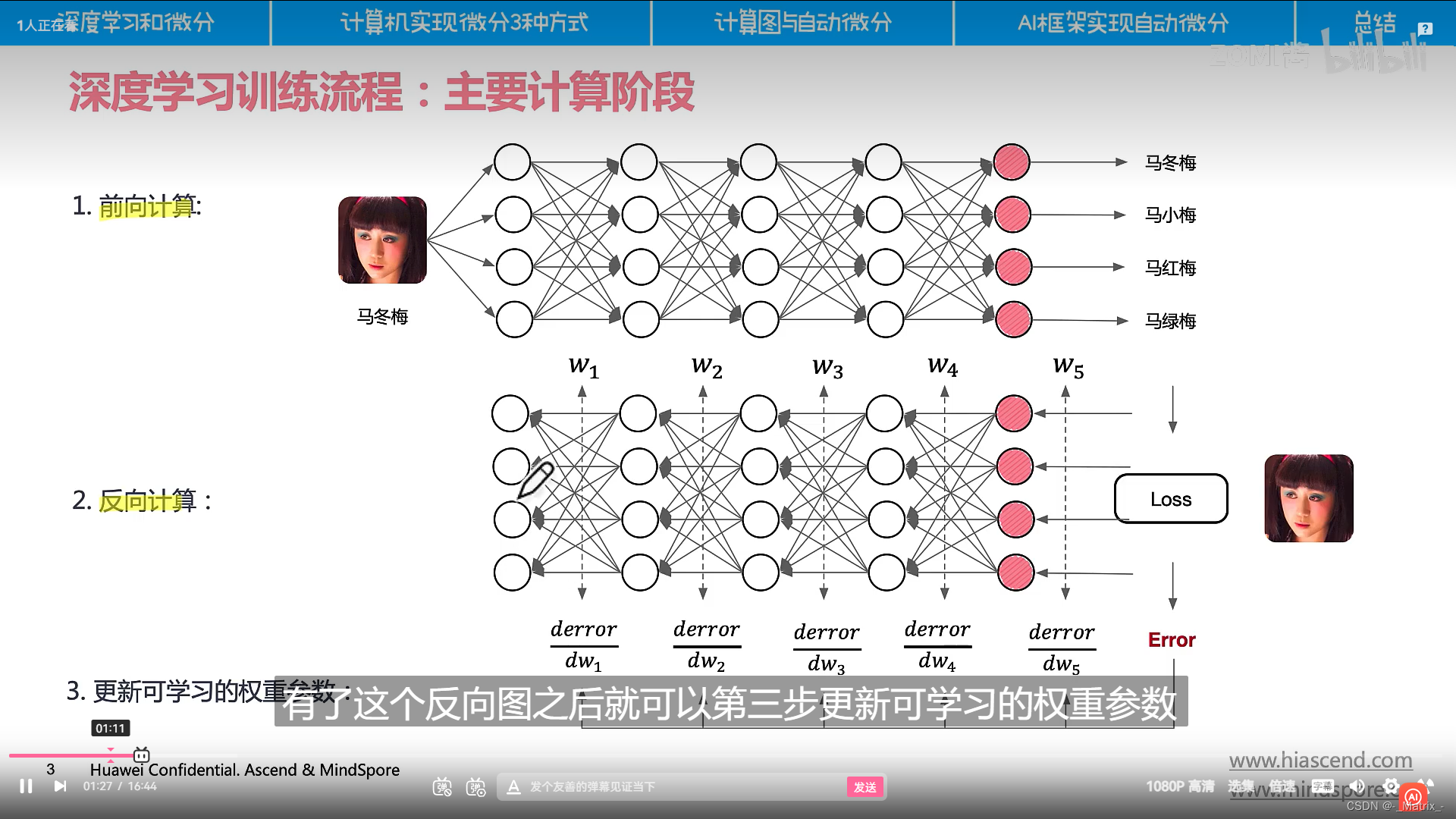
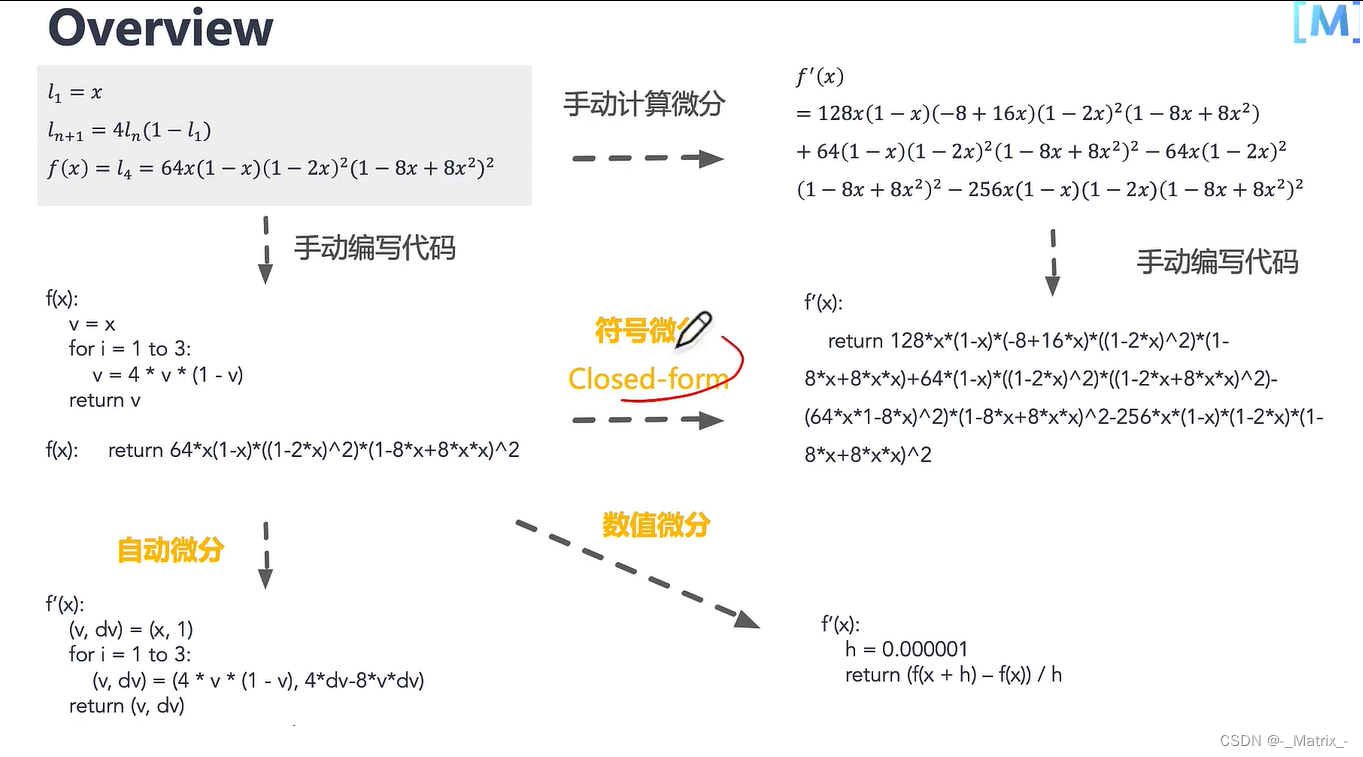
符号微分

符号微分（Symbolic Differentiation）是一种使用数学表达式来表示微分或导数的技术。与数值微分不同，符号微分不是通过逼近来计算导数，而是直接处理数学表达式，得到一个精确的表达式，表示该函数的导数。

符号微分的步骤

1. 表达式定义：首先，你需要一个表达式，例如一个多项式或任何可以微分的数学函数。

2. 应用微分规则：然后，你会应用一系列微分规则（如乘积规则、商规则、链式法则等）来对表达式进行微分。

3. 简化表达式：最后，你可能需要使用一些代数技巧来简化得到的导数表达式。

示例

假设你有一个函数 $f(x)=x^2+3x+2$，并且你想要找到其导数。通过符号微分，你可以应用基本的导数规则：

• $\frac{d}{dx}{x}^n=n\cdot x^{n-1}$
• $\frac{d}{dx}c=0$ （其中 $c$ 是常数）
• 线性函数的导数等于其系数

这样，你可以找到 $f(x)$的导数：

$f^{\prime }(x)=2\cdot x^1+3\cdot 1+0=2x+3$

符号微分在计算图中的使用

在深度学习中，符号微分经常与计算图结合使用：

1. 前向传播：通过计算图表示模型的前向计算。
2. 符号微分：应用符号微分来表示每个操作的局部导数。
3. 反向传播：使用链式法则和计算图中的局部导数来计算整个模型的梯度。

这个过程允许深度学习框架自动计算模型的梯度，这是训练神经网络时所必需的。

总结

符号微分提供了一种精确、直接的方式来计算导数。在深度学习和其他科学计算应用中，通过结合计算图，符号微分使得自动求导和梯度下降优化变得可行和高效。不过，对于非常复杂的表达式，符号微分可能导致表达式膨胀，从而增加了计算复杂性。因此，有时可能会结合使用符号微分和数值微分方法。

数值微分

数值微分是一种近似计算函数导数的技术。与符号微分不同，数值微分不是通过解析地处理数学表达式来找到导数的精确形式，而是使用函数在特定点的数值来估计导数。

前向差分法

最简单的数值微分方法之一是前向差分法。假设你想要计算函数$f(x)$在点$x$处的导数，你可以使用以下公式：

$f^{\prime }(x)\approx \frac{f(x+h)-f(x)}{h}$

其中$h$是一个非常小的正数，称为步长。这个公式给出了在$x$附近的函数的斜率的近似值。

中心差分法

前向差分方法的一个问题是，它可能不是非常精确，特别是当$h$相对较大时。更精确的方法是中心差分法，使用以下公式：

$f^{\prime }(x)\approx \frac{f(x+h)-f(x-h)}{2h}$

中心差分通过计算$f(x)$在$x$附近的两点的平均斜率，通常提供了更好的近似。

数值微分的使用

数值微分用于许多不同的应用领域，包括：

• 解析解不可用：当函数的导数很难或不可能解析地找到时，可以使用数值微分。

• 深度学习的梯度检查：在深度学习中，数值微分通常用于梯度检查，以确保使用符号微分（或自动微分）计算的梯度是正确的。

• 科学和工程应用：数值微分用于许多科学和工程应用，其中需要近似导数，但可能没有解析解。

注意事项

• 选择步长：选择合适的步长$h$是一个关键问题。太大的步长可能会导致近似不精确，而太小的步长可能会导致数值不稳定。

• 数值不稳定：当涉及极小或极大的值时，数值微分可能会出现问题，因为计算机浮点数的精度有限。

• 计算成本：数值微分通常比符号微分更慢，因为它需要多次评估函数。

总结

数值微分是一种有用的工具，特别是当解析解不可用或难以获得时。它提供了一种灵活而实用的方法来近似导数，但必须谨慎选择参数并注意可能的数值问题。在深度学习和其他领域，它通常与符号微分或自动微分结合使用。

自动微分

视频链接：【前向微分和正向微分怎么理解？
自动微分（Automatic Differentiation，简称AD）是一种高效计算函数导数（或梯度）的技术。它不同于数值微分和符号微分，因为它可以提供更高的数值稳定性和计算效率。下面是自动微分的更多细节：

1. 基本原理

自动微分基于链式法则进行，它通过计算机程序来逐步计算和追踪函数的局部导数。基本的想法是将复杂函数分解为一系列简单的元素函数（例如加法、乘法等），并依次计算这些函数的导数。

2. 主要类型

自动微分可以分为两种主要类型：

1. 前向模式（Forward Mode）

在前向模式中，我们从输入向量开始，然后通过每一个操作前进，计算每一步的局部导数和全局雅可比矩阵的相应部分。给定一个函数 $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$，前向模式特别适合 $n\ll m$ 的情况。

2. 反向模式（Reverse Mode）

在反向模式中，我们首先进行一次正向传递来计算函数的输出，然后从输出向后进行一次传递来计算梯度或雅可比矩阵的每一部分。反向模式特别适合于 $n\gg m$ 的情况，这也是为什么它被广泛应用于神经网络和深度学习，因为我们通常有许多输入和少量输出（例如损失函数）。

3. 计算图

自动微分常常依赖于一个计算图来表示和跟踪函数的计算过程。计算图是一种图形数据结构，其中每个节点代表一个操作，每个边代表数据流。

4. 应用

自动微分被广泛应用于各种领域，特别是在机器学习和优化问题中。它是训练神经网络时所用的反向传播算法的核心。

5. 工具和库

现有许多库和框架支持自动微分，如TensorFlow、PyTorch等，它们提供了方便的API来实现和使用自动微分技术。

6. 优点和缺点

• 优点：
  • 高数值稳定性：比数值微分更稳定。
  • 高效：特别是反向模式，它可以高效地计算梯度，尤其是对于有大量输入和少量输出的函数。
• 缺点：
  • 内存消耗：反向模式可能需要大量的内存来存储中间结果。
  • 实现复杂性：实现一个自动微分系统可能是非常复杂和技术性的。

计算图

自动微分通常是在计算图的基础上实现的。在计算图中，一个复杂函数被分解为多个简单的操作，这些操作被组织为一个有向图。现在，让我们更详细地了解自动微分和计算图之间的关系：

1. 计算图的建立

如我们前面所述，首先我们需要建立一个计算图，代表我们的函数。这涉及将函数分解为更简单的操作和变量，然后以有向图的形式表示这些操作和变量。

2. 前向传播

在计算图中，我们从输入变量开始，然后按照图中的顺序进行操作，直到我们计算出输出。这就是所谓的前向传播。

3. 反向传播

反向传播是自动微分的核心。在这一步，我们从输出开始，然后向后计算每一步的局部导数（或梯度）。这通常涉及应用链式法则，这是一种从输出向输入反向传播导数的方法。

4. 链式法则和梯度计算

通过使用链式法则，我们可以计算从输出到任何中间变量或输入的梯度。通过这种方式，我们可以得到我们想要的所有导数，而不是仅仅是输出相对于输入的导数。

5. 优点

• 精确度：自动微分可以提供与解析解几乎相同的精确度。
• 效率：它通常比数值微分方法更快、更稳定，尤其是对于具有许多变量的复杂函数。

例子：

使用给定的函数 $f(x,y)=\log (x)+x\cdot y-\sin (y)$，我们可以构建一个计算图，将该函数分解为多个基本操作。下面是计算图的创建步骤：

步骤1: 定义变量和运算

首先，我们识别并定义所有的基本变量和运算：

1. 变量: $x$, $y$
2. 运算:
   • $\log (x)$
   • $x\cdot y$
   • $\sin (y)$
   • 加法和减法来组合上述结果

步骤2: 创建节点

然后，为每个变量和运算创建节点：

1. 节点1（变量）: $x$
2. 节点2（变量）: $y$
3. 节点3（运算）: $\log (x)$
4. 节点4（运算）: $x\cdot y$
5. 节点5（运算）: $\sin (y)$
6. 节点6（运算）: $\log (x)+x\cdot y$
7. 节点7（运算）: $\log (x)+x\cdot y-\sin (y)$ (这是最终的输出节点)

步骤3: 创建边

接着，我们连接相应的边来形成有向图：

1. 从节点1到节点3（表示 $\log (x)$ 的输入是 $x$）
2. 从节点1到节点4（表示 $x\cdot y$ 的一个输入是 $x$）
3. 从节点2到节点4（表示 $x\cdot y$ 的另一个输入是 $y$）
4. 从节点2到节点5（表示 $\sin (y)$ 的输入是 $y$）
5. 从节点3和节点4到节点6（表示他们的结果被加在一起）
6. 从节点6和节点5到节点7（表示前者的结果减去后者的结果来得到最终输出）

步骤4: 执行前向传播

现在你可以执行前向传播来计算输出，按照操作的顺序一步步前进，直到达到输出节点。

步骤5: （可选）执行反向传播

如果你还打算进行自动微分，你可以实施反向传播算法来计算相对于 $x$ 和 $y$ 的偏导数。

代码实现：

///
/// \brief The Variable class
/// 自动微分
class Variable
{
public://保存值double value;//保存梯度double grad;//当前的梯度是否启用bool isEnableGrad;Variable(double v = 0.0,bool requires_grad=true,double g=0.0) : value(v), isEnableGrad(requires_grad),grad(g){}std::function<void()> backpropFunc;std::vector<std::shared_ptr<Variable>> parents;//设置求导函数void setBackprop(const std::function<void()>& func){backpropFunc = func;}//添加组成当前节点的节点void addParent(const std::shared_ptr<Variable>& parent){parents.push_back(parent);}//反向传播void backward(){if (backpropFunc)backpropFunc();for (auto& parent : parents){parent->backward();}}};//加法
inline std::shared_ptr<Variable> operator+(const std::shared_ptr<Variable>& a, const std::shared_ptr<Variable>& b)
{auto result = std::make_shared<Variable>(a->value + b->value);result->setBackprop([=]() {if(a->isEnableGrad)a->grad += result->grad;if (b->isEnableGrad)b->grad += result->grad;});result->addParent(a);result->addParent(b);return result;
}
//减法
inline std::shared_ptr<Variable> operator-(const std::shared_ptr<Variable>& a, const std::shared_ptr<Variable>& b)
{auto result = std::make_shared<Variable>(a->value - b->value);result->setBackprop([=]() {if (a->isEnableGrad)a->grad += result->grad;if (b->isEnableGrad)b->grad -= result->grad;});result->addParent(a);result->addParent(b);return result;
}//乘法
inline std::shared_ptr<Variable> operator*(const std::shared_ptr<Variable>& a, const std::shared_ptr<Variable>& b)
{auto result = std::make_shared<Variable>(a->value * b->value);result->setBackprop([=]() {if (a->isEnableGrad)a->grad += b->value * result->grad;if (b->isEnableGrad)b->grad += a->value * result->grad;});result->addParent(a);result->addParent(b);return result;
}
// 除法
inline std::shared_ptr<Variable> operator/(const std::shared_ptr<Variable>& a, const std::shared_ptr<Variable>& b)
{if (b->value == 0.0) {std::cerr << "Error: Division by zero!" << std::endl;exit(1);}auto result = std::make_shared<Variable>(a->value / b->value);result->setBackprop([=]() {if (a->isEnableGrad)a->grad += (1.0 / b->value) * result->grad;if (b->isEnableGrad)b->grad -= (a->value / (b->value * b->value)) * result->grad;});result->addParent(a);result->addParent(b);return result;
}
// sin
inline std::shared_ptr<Variable> sin(const std::shared_ptr<Variable>& a)
{auto result = std::make_shared<Variable>(std::sin(a->value));result->setBackprop([=]() {if (a->isEnableGrad)a->grad += std::cos(a->value) * result->grad;});result->addParent(a);return result;
}
// cos
inline std::shared_ptr<Variable> cos(const std::shared_ptr<Variable>& a)
{auto result = std::make_shared<Variable>(std::cos(a->value));result->setBackprop([=]() {if (a->isEnableGrad)a->grad -= std::sin(a->value) * result->grad;  // 注意这里是减号，因为cos的导数是-sin});result->addParent(a);return result;
}// log
inline std::shared_ptr<Variable> log(const std::shared_ptr<Variable>& a)
{if (a->value <= 0.0) {std::cerr << "Error: Logarithm of non-positive number!" << std::endl;exit(1);}auto result = std::make_shared<Variable>(std::log(a->value));result->setBackprop([=]() {if (a->isEnableGrad)a->grad += (1.0 / a->value) * result->grad;  // 导数为 1/x});result->addParent(a);return result;
}// exp
inline std::shared_ptr<Variable> exp(const std::shared_ptr<Variable>& a)
{auto result = std::make_shared<Variable>(std::exp(a->value));result->setBackprop([=]() {if (a->isEnableGrad)a->grad += std::exp(a->value) * result->grad;  // 导数为 e^x});result->addParent(a);return result;
}int main() {auto x = std::make_shared<Variable>(2.0);  // 创建一个初值为2的变量xauto y = std::make_shared<Variable>(5.0,false);  // false 不计算y的梯度auto g = log(x) + x * y - sin(y);g->grad = 1.0;  // df/df = 1g->backward();std::cout << "df/dx = " << x->grad << std::endl;std::cout << "df/dy = " << y->grad << std::endl;return 0;
}