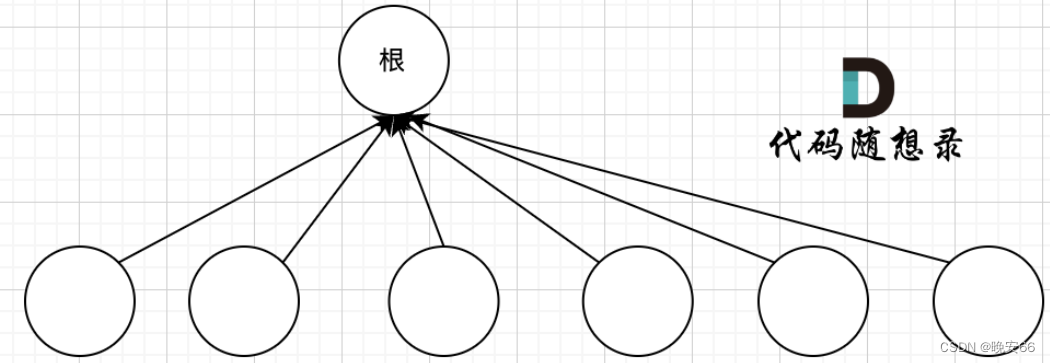
题目比较模板，但是也扩展了许多以前不知道的知识点，记录一下比较有启发性的题。

目录

1.并查集之删除操作---创点转移：

2.并查集之删除操作---逆向思考：

---

1.并查集之删除操作---创点转移：

1和3都是并查集的基础操作，这里就不说了（以前讲过），我们主要看2，我们把2的操作拆分成先去除p，再合并p，那么我们如何删除呢？

我们可以真的去删，但是我们需要修改子节点的连接，会增加时间复杂度并且比较麻烦。

于是我们采用用空间换时间的策略，我们可以再创建一个点，当我们删3时，我们可以保留原来的位置，但是我们需要为3提供真实的点，于是我们用类似映射的方法real[3]=新创建的点，这样子，我们就把3的“空壳”留在原地方，而把3的“灵魂”存在了其他地方，这样其他的点也就不用操作了。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,p,q,c,fa[200010],real1[100005],cc;
struct node{int cnt;long long sum;
}root[200010];
int find(int x){if(fa[x]==x) return x;return fa[x]=find(fa[x]);
}
void merge(int x,int y){root[find(y)].cnt+=root[find(x)].cnt;root[find(y)].sum+=root[find(x)].sum;fa[find(x)]=find(y);
}
void del(int x){root[find(real1[x])].cnt--;root[find(real1[x])].sum-=x;real1[x]=++cc;root[cc].cnt=1;root[cc].sum=x;fa[cc]=cc;}
signed main(){while(cin>>n>>m){for(int i=1;i<=n;i++){fa[i]=i;real1[i]=i;root[i].cnt=1;root[i].sum=i;}cc=n;for(int i=1;i<=m;i++){cin>>c;if(c==1){cin>>p>>q;if(find(real1[p])==find(real1[q])) continue;merge(real1[p],real1[q]);}else if(c==2){cin>>p>>q;if(find(real1[p])==find(real1[q])) continue;del(p);merge(real1[p],real1[q]);}else{cin>>p;node ss=root[find(real1[p])];cout<<ss.cnt<<" "<<ss.sum<<endl;}}}
}

这里有几点需要注意：

1.多组输入注意对会新创建的值的改变，这里的cc每次都应从n开始。

2.注意合并时的判断条件必不可少，因为这里的并查集带了权值，重复时会导致值的重复相加。

2.并查集之删除操作---逆向思考：

以前有讲过，这里找到了个题目算是填坑了。我们先记录删的，把删的全删了，这样从反方向就是创建了。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,x,y,k,fa[400010],huei[400010],head[400010],cnt,ck[400010];
int hh[400010];
struct node{int dian,next;
}edge[400010];
void merge(int x,int y){edge[++cnt].dian=y;edge[cnt].next=head[x];head[x]=cnt;
}
int find(int x){if(fa[x]==x) return x;return fa[x]=find(fa[x]);
}
void merge1(int x,int y){fa[find(x)]=find(y);
}
int main(){cin>>n>>m;memset(head,-1,sizeof(head));for(int i=1;i<=m;i++){scanf("%d%d",&x,&y);merge(x,y);merge(y,x);}cin>>k;for(int i=1;i<=k;i++){scanf("%d",&huei[i]);ck[huei[i]]=1;}for(int i=0;i<=n-1;i++) fa[i]=i;for(int i=0;i<=n-1;i++){if(ck[i]==1) continue;if(head[i]==-1) continue;for(int j=head[i];j!=-1;j=edge[j].next){if(ck[edge[j].dian]==1) continue;if(find(edge[j].dian)==find(i)) continue;merge1(edge[j].dian,i);}}int cc=0;for(int i=0;i<=n-1;i++){if(fa[i]==i&&ck[i]==0) cc++;}hh[k+1]=cc;for(int i=k;i>=1;i--){int gg=huei[i];ck[gg]=0;cc++;for(int j=head[gg];j!=-1;j=edge[j].next){if(ck[edge[j].dian]==1) continue;if(find(edge[j].dian)!=find(gg)) cc--;	merge1(edge[j].dian,gg);}hh[i]=cc;}for(int i=1;i<=k+1;i++){printf("%d\n",hh[i]);}
}