"Success is not the key to happiness. Happiness is the key to success. If you love what you are doing, you will be successful."

- Albert Schweitzer

1. 题目描述

2.  题目分析与解析

2.1 思路一——暴力求解

暴力求解是比较干脆果断的一种解决问题的方式，本质上就可以被描述为一个一个找。对于这个题目，暴力求解思路很简单：

1. 外层遍历数组 nums的每一个元素A

2. 内层遍历数组 nums该元素后面的元素（前面的无需遍历是因为前面的元素作为A时已经判定过了）

3. 将这两个数进行求和，判断是否能够等于target

但是这种求解方法时间复杂度很显而易见时O(N^2)，因此我们想一想有什么其它的解决思路。

2.2 思路二——存储下标排序后匹配

不知道大家之前有没有做过关于判断一个数组种有没有两数之和等于target的题目，就是这个题目：

两数之和 II - 输入有序数组

我的解析文章链接为：

面试经典150题——两数之和 II - 输入有序数组

在这篇文章种我讲的很详细，大家先看一下上面这篇文章。但它题目中给的是有序数组，这里我们得到的是无序数组，那么我们是不是就可以稍微进行处理，变成有序数组，然后找到两个数之和等于target的两个元素，找到他们的原始下标返回。

注意：这里是原始下标

因此我们是不是就先需要使用一个结构存储每个元素的原始下标，然后再按照上述思路进行处理，就可以在O(N^2)时间复杂度内求解。

代码思路：

1. 使用一个映射存储原始元素及其下标

2. 通过双指针方式，从头尾遍历，具体图解见上面链接提到的文章，讲的很详细

3. 找到两个指针指到的元素等于target，根据原始元素及其下标映射找到他们的原始下标并返回

2.3 思路三——存储下标直接寻找匹配项

现在我们再来想一想，既然我需要求出两个数字之和等于target，那么我如果确定了一个加数，被加数是不是也能确定？

因为被加数就等于target减去加数。因此我是不是就可以先从头到尾遍历一次数组，将每一个元素及其下标先存储起来，然后我再看每一个元素的被加数？如果能够匹配，就把这两个元素的下标返回。

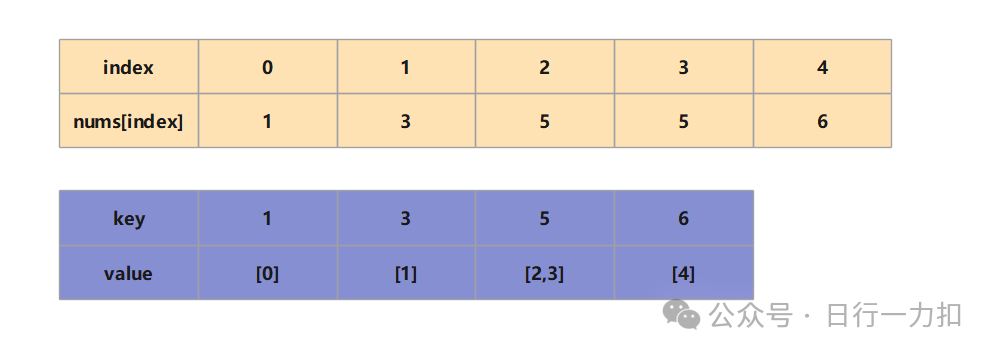
但是考虑一下对于数组：【1，3，5，5，6】，如果我的target=10，那么两个5怎么办？

因此我们hashmap的值应该是一个list，来存储相同大小元素的下标。如下图：

代码思路：

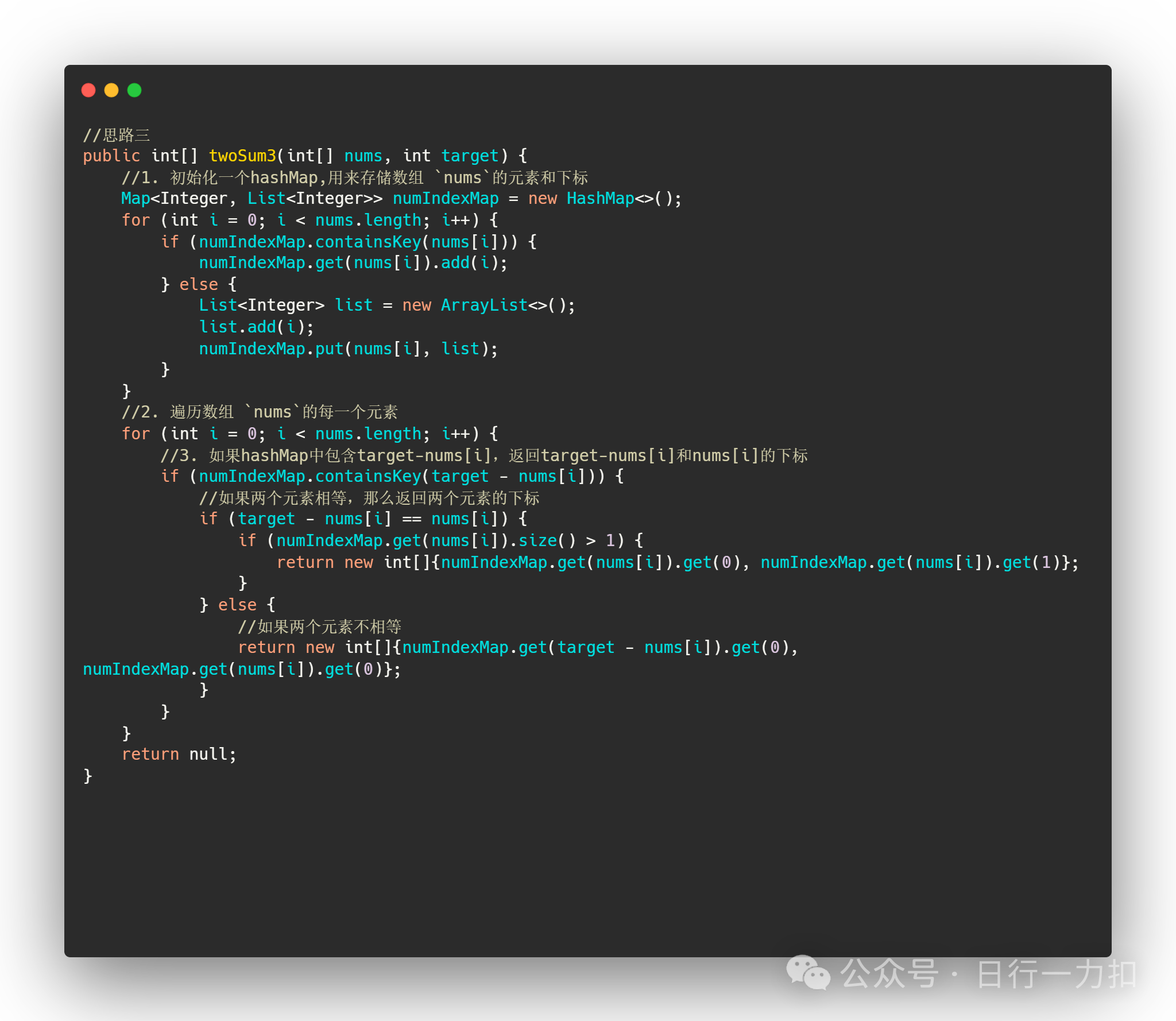
1. 初始化一个hashMap,结构为：Map<Integer, List<Integer>> 用来存储数组 nums的元素和下标

2. 遍历数组 nums的每一个元素

3. 如果hashMap中包含target-nums[i]，返回target-nums[i]和nums[i]的下标

   • 在这里需要判读这两个数是否相等，如果两个元素相等，那么返回两个元素的下标就是如上图所示

   • 如果两个元素不相等那么就返回对应的value列表的第一个元素

2.4 思路四——直接匹配

现在我们思考一下，如果我们需要找到target的两个加数，那么这两个加数肯定有出现的先后次序对不对？他们肯定不可能拥有相同的下标，所以对于两个加数A，B，要么A的下标大，要么B的下标大。

其次，如果我们走过了较小下标的那个加数，假设我们将它存储了起来，那么是不是走到较大下标加数时，只需要判断之前有没有走过某一个加数能够匹配，实现 A+B=target ?

而这个判断过程并不需要再回过头去看之前走过的数字，因为我们需要的匹配是一个很精准的匹配，就是找 target-B，也就是找一个数。如果我们对于已经走过的每一个数都进行了hash，那么是不是就可以再O(1)时间找到该数？

所以可以有如下：

代码思路：

1. 初始化一个hashMap，键为数值，value为位置

2. 遍历nums的每一个数，尝试找到与之匹配的target-B是否在hashMap中存在

   • 如果存在，就将这两个下标返回

   • 如果不存在，就先将该元素及其下标放入hashMap（假设存在解且它是加数，那么他后面肯定有一个被加数）

3. 都找不到返回null

3. 代码实现

3.1 思路一

3.2 思路二

3.3 思路三

3.4 思路四

4. 相关复杂度分析

​解法一（暴力枚举）

• 时间复杂度: (O(n^2))。因为这个解法涉及到一个双重循环遍历所有元素的组合，对于每对元素组合，它检查它们的和是否等于目标值。

• 空间复杂度: (O(1))。这个方法只使用了固定的额外空间（用于存储结果和循环变量）。

解法二（排序后使用双指针）

• 时间复杂度: (O(n log n))。主要的时间开销来自于排序操作，而双指针遍历的时间复杂度为 (O(n))。

• 空间复杂度: (O(n))。这个方法需要额外的空间来存储元素到其索引列表的映射，以及处理可能存在的重复元素。

解法三（使用哈希表存储元素和索引，改进的遍历）

• 时间复杂度: (O(n))。每个元素被遍历两次，并且哈希表的查找操作时间复杂度为 (O(1))。因此，总的时间复杂度是线性的。

• 空间复杂度: (O(n))。需要额外的空间来存储元素到其索引列表的映射，用于处理重复元素和实现快速查找。

解法四（使用哈希表存储元素和索引，即时检查）

• 时间复杂度: (O(n))。与解法三相似，这个方法通过遍历数组一次，并在遍历过程中使用哈希表来检查是否存在满足条件的元素对，从而达到线性时间复杂度。

• 空间复杂度: (O(n))。这个方法同样需要额外的空间来存储元素到其索引的映射，其空间复杂度也是基于输入数组的大小。

综上所述，解法一是时间复杂度最高的方法，不适合大数据集。解法二和解法二修改版虽然在时间上有所改进，但仍受到排序步骤的限制。解法三和解法四提供了最优的时间复杂度解决方案，且解法四在实际应用中更为直观和高效，因为它无需事先处理所有元素，而是在遍历过程中即时查找并返回结果。