创建时间：2024-02-23
最后编辑时间：2024-02-24
作者：Geeker_LStar

你好呀~这里是 Geeker_LStar 的人工智能学习专栏，很高兴遇见你~
我是 Geeker_LStar，一名初三学生，热爱计算机和数学，我们一起加油~！
⭐(●’◡’●) ⭐
那就让我们开始吧！

在上一篇 【初中生讲机器学习】11. 回归算法中常用的模型评价指标有哪些？here! 中，我说我要单开一篇讲讲 “似然”。诺，这不就来了嘛~！
在机器学习里，似然是个蛮重要的概念，但也的确不太好理解，我们来看看吧~

似然和概率

嗯，提到 “似然（likelihood）”，那就不得不说说它的好基友 “概率（probability）” 了。这俩经常被混为一谈（甚至某些教科书都这么写），但实际上，至少在统计学和机器学习里，它俩的区别还是很大的。

从一个简单但经典的例子入手：

概率：
有一个箱子，装有除颜色外都相同的黑色球和白色球共 100 个，其中黑色球有 90 个，白色球 10 个，现在从箱子中任取一个球，结果是黑色球的概率？

这个很简单，90/100*100% = 90% 嘛，这个球是黑球的概率就是 90% 了。
从这个例子可以看出，“概率” 是什么，就是在你已经知道了前提条件（球的总数和颜色分布）的时候，计算某一种特定情况（黑球）出现的可能性。
专业一点，“概率” 是针对概率空间中的某一个事件而言的。

再来看似然。

似然：
有一个箱子，装有除颜色外都相同的黑色球和白色球共 100 个，其中一种颜色的球 90 个，另一种颜色的球 10 个。现在从箱子中任取一球，结果是黑色球，则箱中黑色球是 90 个可能性是多少？

先不说具体怎么计算，但至少从直觉上来讲，你应该会觉得 “黑色球是 90 个的可能性” 大于 “白色球是 90 个的可能性”。因为你这次摸出的是黑色球，而人们总是会倾向于认为 “已经发生的事情发生的概率大”。就比如，如果你再摸几个（摸完放回去），发现一连摸出了 10 个白色球，那或许就会认为黑色球是 10 个，而白色球是 90 个了。ok 不过这个等到极大似然估计那里再细说。

这个例子想要说明什么呢？yes，似然和概率的差别就在于，“似然” 是对于参数而言的（比如球的总数和颜色分布），它可以大致概括为 “在当前结果（现象）出现的情况下，参数是某种情况的可能性”。
概率和似然的关系，类似贝叶斯那篇中讲过的条件概率 $P(A|B)$ 和后验概率 $P(B|A)$ 之间的关系。概率是从参数（条件）推到现象（结果），似然是从现象（结果）推到参数（条件）。

从这里再延伸一点，讲一下似然函数和概率密度函数（或概率质量函数）的区别与联系。
简单讲一下概率密度（质量）函数：如果一个变量是离散的，它取不同值时的概率是一个个点而不是一条连续的曲线，那么就称它的概率函数为概率质量函数；而如果这个变量是连续的，即它取不同值时的概率能够组成一条连续的曲线，那么就称它的概率函数为概率密度函数，一个典型的概率密度函数（正态分布）如下图：

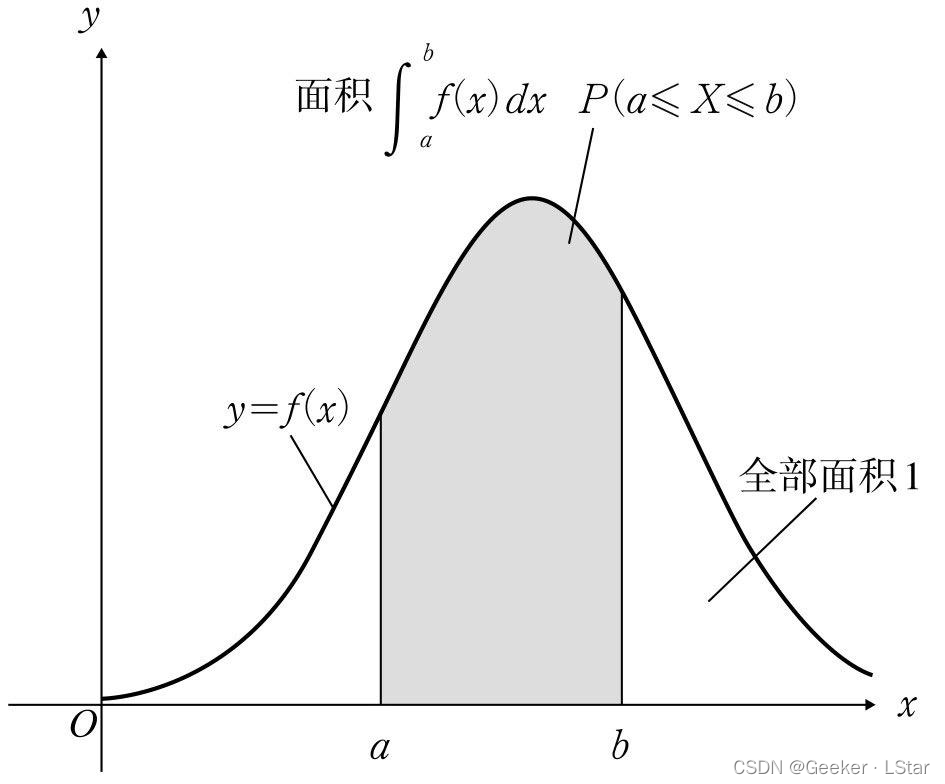
虽然我们还没有讲似然函数，但是从似然和概率在定义上的不同也可以猜到一二：似然函数的自变量是参数，概率密度（质量）函数的自变量是现象（结果）。似然函数告诉我们，在现象（结果）已知的情况下，参数取值为某种情况的可能性是多少，而概率密度（质量）函数告诉我们，在参数已知的情况下，某种现象（结果）出现的可能性是多少。
它们两个正好反过来。

似然函数

好，热身完毕，我们现在来看看似然函数到底是什么。

数学推导

先上数学定义，后面详细推：
$$L(\theta |x)=P(x|\theta )$$其中，$L(\theta |x)$ 是似然函数，$P(x|\theta )$ 是在条件（参数）$\theta$ 下，$x$ 发生的概率。
来推导一下，和贝叶斯那篇的推导很相似。为了方便，我们把参数定义为 B，现象定义为 A。那么我们要求的似然函数就是：$$L(B|A)=P(B|A)=\frac{P(A,B)}{P(A)}=\frac{P(A|B)P(B)}{P(A)}$$

嘿嘿嘿是不是和贝叶斯那个很像~
我们知道，事件 A 已经发生了（我们之前说过，“似然” 表示某个现象（结果）产生时，参数是某种情况的可能性），所以 $P(A)$ 直接等于 1 了，so 和朴素贝叶斯一样，现在又变成联合概率的事情了，即 $P(B|A)=P(A|B)P(B)$.

好，再继续往下之前，我们需要明确一件事——计算似然函数的目的并不是要知道这个值到底是多少，似然函数本身的数值没什么意义，重要的是比较不同参数的似然函数大小，似然函数最大的那个参数就是最符合当前现象（结果）的参数。

知道这一点之后再去看之前的式子，我们不用管 $P(A|B)P(B)$ 到底是多少，我们只需要得到使得 $P(A|B)P(B)$ 最大的 $A$ 值就可以。所以，$P(B)$ 是多少不重要，直接忽略它就好。

so 最后得到的结果就是 $L(\theta |x)=P(x|\theta )$，不过我们可以做进一步的展开。
分两种情况，x，注意不是参数 θ 而是 x，是离散型还是连续型（不过本质上没什么区别）。
先说连续型吧，在概率和贝叶斯的那篇中我讲过，假设各个参数彼此独立，那么有：
$$L(\theta |x)=P(x|\theta )=f(x_1,x_2,...,x_n|\theta )=\prod _{i=1}^{n}f(x_i|\theta )$$这坨东西在数值上等于各个观测值 x 的概率密度函数值的乘积。但是，需要明确的是，虽然似然函数和概率密度函数在形式上一致，但是它们并不等价（意思同 “函数的等价”）。 概率密度函数的自变量是观测值，而似然函数的自变量是参数，它描述的是在给定结果的条件下参数出现的可能性。

离散型的也好办，公式就是 $\prod _{i=1}^{n}P(x_i|\theta )$，在形式上和概率质量函数等价。

一个例子

用一个抛硬币的例子来理解上面讲的那些。

有一枚硬币，抛出后正面朝上的概率为 P，反面朝上的概率为 1-P。现在抛这种硬币 10 次，共有 6 次正面朝上，问 P 的值最有可能是多少？

显然，这是一个关于似然的问题，思路大致如下：

1. 计算不同 P 值的似然度，即在当前结果的条件下，不同 P 值的可能性。
2. 似然度最大的 P 值，即最有可能的 P 值。

顺着这个思路来算一下，记硬币正面向上为 H：
第一种情况，P=0.5，也就是硬币正反面朝上的概率相等（经典情况，均匀的硬币），我们要求 $L(0.5|6H)$，根据 $L(\theta |x)=P(x|\theta )$，我们只需计算 $P(6H|0.5)$，即在 P=0.5 的时候，10 次中有 6 次正面朝上的概率。

嗯，典型的二项分布（之前说过，关于各种分布会单独开一篇讲），二项分布的公式：$$likelihood(X=k)=C_n^k{P}^k(1-P{)}^{n-k}$$其实如果学过排列组合的话应该还算好理解，前面的 $C_n^k$ 就是组合数，后面的 $P^k(1-P{)}^{n-k}$ 就是某一种符合要求的情况出现的概率。

先来算一下 P=0.5，其中 k = 6。$likelihood(P=0.5)=C_{10}^{6}0.5^{6}0.5^4=210\ast 0.5^{1}0\approx 0.20508$，也就是说，在 “10 次中有 6 次正面朝上” 这个事件发生的条件下，“硬币正面朝上的概率 P 为 0.5” 的似然度是 0.2 左右。
注意，这不是说 “6 次正面朝上” 的概率是 0.2 左右，而是 “在 6 次正面朝上” 的结果下，P=0.5 的似然度（可能性）是 0.2，这两者并没有直接关系。
说过啦，这个数值本身不重要，重要的是和其它 P 值的似然度的比较。

再来看看 P=0.6，公式 $likelihood(P=0.6)=C_{10}^{6}0.6^{6}0.4^4\approx 0.25082$，也就是说 “硬币正面朝上的概率 P 为 0.6” 的似然度是 0.25，高于 P=5 时，换言之，P=0.6 比 P=0.5 时更有可能出现当前结果。

那么 P=0.7 呢？答案是 0.20012 左右，不如 P=0.6 的时候。并且根据二项分布的图像（后几篇里会讲），P=0.8、0.9 等等的时候，似然度只会继续降低。

代码实现

嗯，但是我们肯定不可能把所有的 P 值的情况都算一遍，so 代码 & 可视化走起：

# 似然函数——可视化
import numpy as np
import matplotlib.pyplot as plt
import math# 定义似然函数
# n：实验次数；k：成功次数；p：成功概率
def likelihood(n, k, p):# 组合数 * 一种符合要求的情况的概率return math.comb(n, k) * (p ** k) * ((1-p) ** (n-k))# 生成自变量（成功概率，也就是参数）的取值范围
x = np.linspace(0, 1, 100)
# 计算对应的因变量（似然）的取值
y = [likelihood(10, 6, i) for i in x]# 绘制曲线图
plt.plot(x, y)
plt.title('Likelihood Function')
plt.xlabel('P')
plt.ylabel('Likelihood')
plt.show()

x=\dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}.

结果图如下，红线是似然函数值最大的参数，大概在 0.6 左右。也就是说，在当前结果下，“P = 0.6” 是最有可能的参数，它最能解释当前的结果。

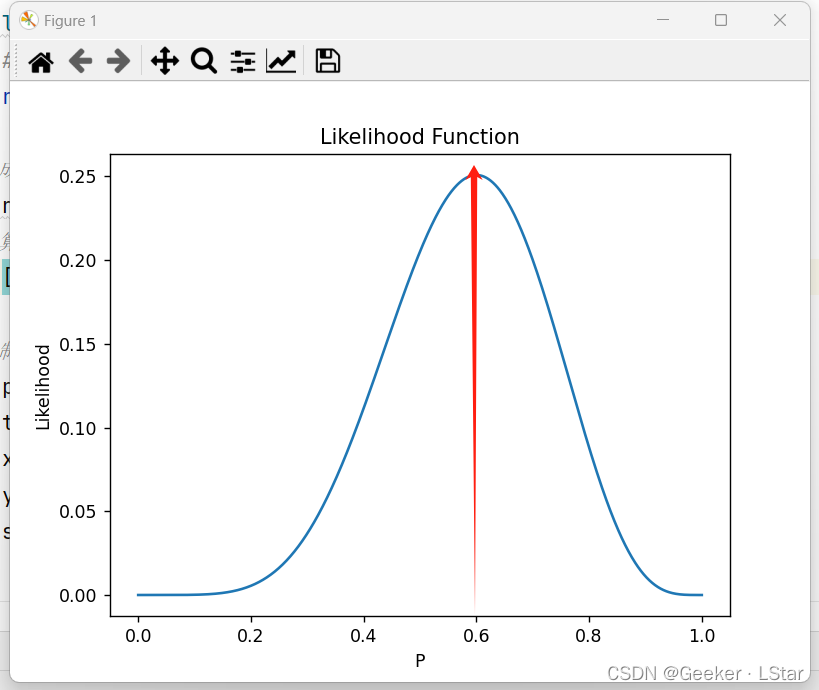
图应该就清晰多了。总而言之，关于似然函数，下面这些是重点：
似然函数的自变量是参数，它衡量的是在某种结果下某种参数的合理性（或这种参数出现的可能性）。似然函数本身的值并不重要，重要的是哪种参数的似然函数最大。一般而言，似然函数最大的参数对模型的解释性最强。

极大似然估计

好，终于把似然和似然函数讲完了（我感觉讲的挺明白的），接下来来看一个重要的应用——极大似然估计。

极大似然估计，英文全称 Maximum Likelihood Estimation，简称 MLE。

一句话概括核心思想：已经发生的事情发生的概率大。
好好好，这句话的确说的奇奇怪怪的，不过解释完你就懂了~
假设我们现在在训练一个模型，我们知道一堆样本 $X=(X_1,X_2,...,X_n)$，它们的观测值分别为 $x=(x_1,x_2,...,x_n)$（啊对我觉得还是规范一下书写比较好，，，要不然写着写着就乱了），我们的目标就是给这个模型找到参数。
那么，什么样的参数最好呢？这不用问了，我们肯定要求参数对训练集的解释性强，即参数可以让模型较好的拟合训练集，因为要是连训练集都拟合不好，还怎么泛化。所以，我们要选择似然函数值最大的那个（或那组）参数。这个过程就被称为极大似然估计。换言之，极大似然估计就是利用已知的样本及结果信息，反推最有可能让这些结果出现的模型参数值。

用数学表达就是：
$$\theta =argmax\theta L(X=x|\theta )$$

数学推导

不用抛硬币的例子了，二项分布不如正态分布好理解，我们用正态分布来举例吧。
关于正态分布，在线性回归原理那一篇中有讲过，后面还会再开一篇讲分布，这里不再细说。
我们假设有一堆样本，其值服从正态分布（也就是说我们可以用一个正态曲线去拟合它们），我们要做的是找到这个正态曲线的平均值和标准差。
换言之，我们要找到一组平均值和标准差，它们描述的正态曲线可以最好地拟合已知样本。
怎么办？yesyes，极大似然估计嘛，我们让似然函数最大就 ok！

根据上一部分讲的公式，似然函数是：
$$L(\mu ,{\sigma }^2|x)=P(x|\mu ,{\sigma }^2)=f(x_1,x_2,...,x_n|\mu ,{\sigma }^2)=\prod _{i=1}^{n}f(x_i|\mu ,{\sigma }^2)$$再根据正态分布的概率密度函数，进一步得到：
$$likelihood=\prod _{i=1}^{n}f(x_i|\mu ,{\sigma }^2)=\prod _{i=1}^n\frac{1}{\sqrt{2\pi }\sigma }{\mathrm{e}}^{-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}}$$我们要求的就是等号最右边那个式子的最大值！

emm 不过，局势目前并不太好（），因为连乘算起来好麻烦。。。
好吧好吧，怎么把乘法变成加法呢？或许 ${\log }_{a}M+{\log }_{a}N={\log }_a(M+N)$ 会给你一点启发——没错，我们可以在等式两边同时取对数呀！并且，让似然函数最大，和让似然函数的对数最大，是等价的。
插一句，通过取对数把连乘的式子转换为求和的形式，这种方法很常用。

有了 $\ln$ 的帮助（没错这叫对数似然函数），式子变成了下面这样：
$$\ln (likelihood)=\sum _{i=1}^n\ln \left(\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}}\right)$$

进一步化简，得到 $$\ln (likelihood)=\sum _{i=1}^n\ln 1-\sum _{i=1}^n\ln (\sigma \sqrt{2\pi })+\sum _{i=1}^n\ln e^{-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}}$$

那么最终结果就是：$$\ln (likelihood)=-n\ln (\sigma \sqrt{2\pi })-\sum _{i=1}^n\frac{(x_i-\mu {)}^2}{2{\sigma }^2}$$

ok！我们现在只需要让这个式子取得最大值就完美了~！
嗯，怎么办，老方法，求偏导啊（（（
先对平均值 $\mu$ 求：
$$\begin{gathered} \frac{\partial }{\partial \mu }(-n\ln (\sqrt{2\pi }\sigma )-\sum _{i=1}^n\frac{(x_i-\mu {)}^2}{2{\sigma }^2}) \\ =\sum _{i=1}^n\frac{2(x_i-\mu )}{2{\sigma }^2} \\ =\sum _{i=1}^n\frac{x_i-\mu }{{\sigma }^2} \end{gathered}$$

再对标准差 $\sigma$ 求：
噗哈哈哈我当时求这个的时候，因为忘了 $\sigma$ 在分母上，所以有两次求出来的偏导的分母中的 $\sigma$ 的次数是 1 啊呃呃呃（（（）。
$$\begin{gathered} \frac{\partial }{\partial \sigma }(-n\ln (\sqrt{2\pi }\sigma )-\sum _{i=1}^n\frac{(x_i-\mu {)}^2}{2{\sigma }^2}) \\ =-\frac{n}{\sigma }+\sum _{i=1}^n\frac{(x_i-\mu {)}^2}{{\sigma }^3} \end{gathered}$$

ok~！偏导不难，解出来结果如下：
$$\{\begin{array}{c}\frac{\partial }{\partial \mu }={\sum }_{i=1}^n\frac{x_i-\mu }{{\sigma }^2}\\ \frac{\partial }{\partial \sigma }=-\frac{n}{\sigma }+{\sum }_{i=1}^n\frac{(x_i-\mu {)}^2}{{\sigma }^3}\end{array}$$

回到最开始的目的——求似然函数的最大值，嗯，那就让两个偏导都等于 0 就 ok 了~~（啊呃，其实这里可以用二阶偏导小于 0 来说明确实是最大值，不过我懒。。）
也就是：
$$\{\begin{array}{c}{\sum }_{i=1}^n\frac{x_i-\mu }{{\sigma }^2}=0\\ -\frac{n}{\sigma }+{\sum }_{i=1}^n\frac{(x_i-\mu {)}^2}{{\sigma }^3}=0\end{array}$$

这两个很好解。
上面那个 $\mu$ 就是 ${\sum }_{i=1}^n{x}_i={\sum }_{i=1}^n\mu$，解出 $\mu =\frac{{\sum }_{i=1}^n{x}_i}{n}$，也就是说，$\mu$ 的极大似然估计就是这堆样本的平均值！
怎么说，你可能会想，$\mu$ 这个东西本来不就是平均值吗？我又用极大似然估计给它解出来一遍是干什么，，，nonono，$\mu$ 本身表示的是正态曲线的平均值，我们事先不知道正态曲线的平均值应该是多少的，但是用极大似然估计推出来它就等于目前这些样本的平均值，这正好反映了极大似然估计就是在 “把对当前结果拟合最优的参数选择为模型参数” 呀！

下面那个 $\sigma$ 就是 $n=\frac{(x_i-\mu {)}^2}{{\sigma }^2}$，解出来 $\sigma =\sqrt{\frac{(x_i-\mu {)}^2}{n}}$，也就是这堆样本的标准差。

那么，如果不是正态分布，而是其它任意一种形式的数据（甚至有可能我们都不知道它是哪种形式的），比如后面会讲的逻辑回归，有没有一个 “通法” 呢？
当然是有的啦！

first，我们得知道这个数据集应该用什么算法去拟合（不知道就散点图看一下 or 多尝试几个），比如到底是线性回归（一元 or 多元？）还是逻辑回归？
second，每种算法都有一个带参数的式子，比如多元线性回归是 $y=w_1{x}_1+w_2{x}_2+...+w_n{x}_n+b$，按照之前给的那个 $L(\theta |x)=P(x|\theta )$，把 $P(x|\theta )$ 的表达式写出来，如果有需要再取个对数把连乘换成求和，如果还有需要也可以把最大化问题转化为负数最小化问题（负对数似然函数）。
third，求极值。方法很多，最常规的就是对求和函数中的每一个参数分别求偏导，令偏导等于 0，解得每一个参数的值。也可以用梯度下降法、牛顿法等方法。

不过，咳咳咳（）（）（）一般有内置函数的（）（）不过如果哪天你心血来潮想训练一下自己求偏导的水平其实这也不失为一个好方法（（（bushi）。

代码实现

我们用代码来实现一个正态分布曲线的极大似然估计。

import numpy as np
from scipy.stats import norm
from scipy.optimize import minimize# 生成一些正态分布的样本数据
np.random.seed(218)    # 随机种子
mu_true = 2.0    # 真实的均值
sigma_true = 1.5    # 真实的标准差
sample_size = 1000    # 样本数量
data = np.random.normal(mu_true, sigma_true, sample_size)# 极大似然估计的目标函数
def neg_log_likelihood(params, data):"""负对数似然函数，用于最小化参数：- params：包含均值和标准差的参数数组- data：观测到的样本数据返回：- 负对数似然函数的值"""mu, sigma = params  # 提取均值和标准差ll = -np.sum(norm.logpdf(data, loc=mu, scale=sigma))  # 计算负对数似然函数值return ll# 初始参数猜测值
initial_guess = [1.0, 1.0]    # 初始均值和标准差的猜测值
# 极大似然估计：使用 L-BFGS-B 方法最小化负对数似然函数
result = minimize(neg_log_likelihood, initial_guess, args=(data,), method='L-BFGS-B')
# 提取估计得到的均值和标准差
mu_mle, sigma_mle = result.x  # 提取估计的均值和标准差
# 打印结果
print("真实均值：", mu_true)
print("估计的均值：", mu_mle)
print("真实标准差：", sigma_true)
print("估计的标准差：", sigma_mle)

注释里面已经写的比较详细了，这里再来解释一下吧~
代码中的方法和我们推导的时候使用的方法有一点细微的差别（但在思想上是一样的），我在代码中计算的是负对数似然函数，因为它可以直接使用 numpy 库中的 L-BFGS-B 算法进行最小化。
L-BFGS-B 算法是优化算法的一种，类似的还有牛顿法等。
（插一句，numpy 这个库简直太 wonderful 了！！）

来看一下结果，极大似然估计的效果还是非常棒的！

---

okkkk！！大功告成~！虽然但是偏导也没那么难哈哈哈哈哈哈 ~

这篇文章分析了似然函数和极大似然估计，并给出了对应代码，希望对你有所帮助！⭐
欢迎三连！！一起加油！🎇
——Geeker_LStar