神经网络
人工神经网络( Artificial Neural Network , 简写为 ANN )也简称为神经网络( NN ),是一种模仿生物神经网络结构和 功能的计算模型 。人脑可以看做是一个生物神经网络,由众多的 神经元 连接而成。各个神经元传递复杂的电信号,树突 接收到输入信号 ,然后对信号进行处理,通过轴突 输出信号。下图是生物神经元示意图:那怎么构建人工神经网络中的神经元呢?

那怎么构建人工神经网络中的神经元呢?

这个过程就像,来源不同树突 ( 树突都会有不同的权重 ) 的信息 , 进行的加权计算 , 输入到细胞中做加和,再通过激活函数输出细胞值。
接下来,我们使用多个神经元来构建神经网络,相邻层之间的神经元相互连接,并给每一个连接分配一个强度,如下图 所示:

神经网络中信息只向一个方向移动,即从输入节点向前移动,通过隐藏节点,再向输出节点移动。其中的基本部分是 :
1. 输入层 : 即输入 x 的那一层
2. 输出层 : 即输出 y 的那一层
3. 隐藏层 : 输入层和输出层之间都是隐藏层
特点是:
• 同一层的神经元之间没有连接。
• 第 N 层的每个神经元和第 N-1 层 的所有神经元相连(这就是 full connected 的含义 ) ,这就是全连接神经网络。
• 第 N-1 层神经元的输出就是第 N 层神经元的输入。
• 每个连接都有一个权重值( w 系数和 b 系数)。
激活函数
激活函数 用于对每层的 输出数据进行变换 , 进而为整个网络注入了 非线性因素 。此时, 神经网络就
可以拟合各种曲线。
1. 没有引入非线性因素的网络等价于使用一个线性模型来拟合
2. 通过给网络输出增加激活函数, 实现引入非线性因素, 使得网络模型可以逼近任意函数, 提升网
络对复杂问题的拟合能力.
如果不使用激活函数,整个网络虽然看起来复杂,其本质还相当于一种 线性模型
1.sigmoid激活函数

• sigmoid 函数可以将 任意的输入 映射到 (0, 1) 之间,当输入的值大致在 <-6 或者 >6 时,意味着输入任何值得到的激 活值都是差不多的,这样会丢失部分的信息。比如:输入 100 和输出 10000 经过 sigmoid 的激活值几乎都是等于 1 的,但是输入的数据之间相差 100 倍的信息就丢失了。
• 对于 sigmoid 函数而言,输入值在 [-6, 6] 之间输出值才会 有明显差异 ,输入值在 [-3, 3] 之间才会 有比较好的效果 。
• 通过上述导数图像,我们发现导数数值范围是 (0, 0.25) ,当输入 <-6 或者 >6 时, sigmoid 激活函数图像的 导数接近 为 0 ,此时 网络参数将更新极其缓慢,或者无法更新。
• 一般来说, sigmoid 网络在 5 层之内 就会产生 梯度消失 现象。而且,该激活函数并不是以 0 为中心的,所以在实践 中这种激活函数使用的很少。sigmoid 函数一般只用于二分类的输出层 。
tanh激活函数
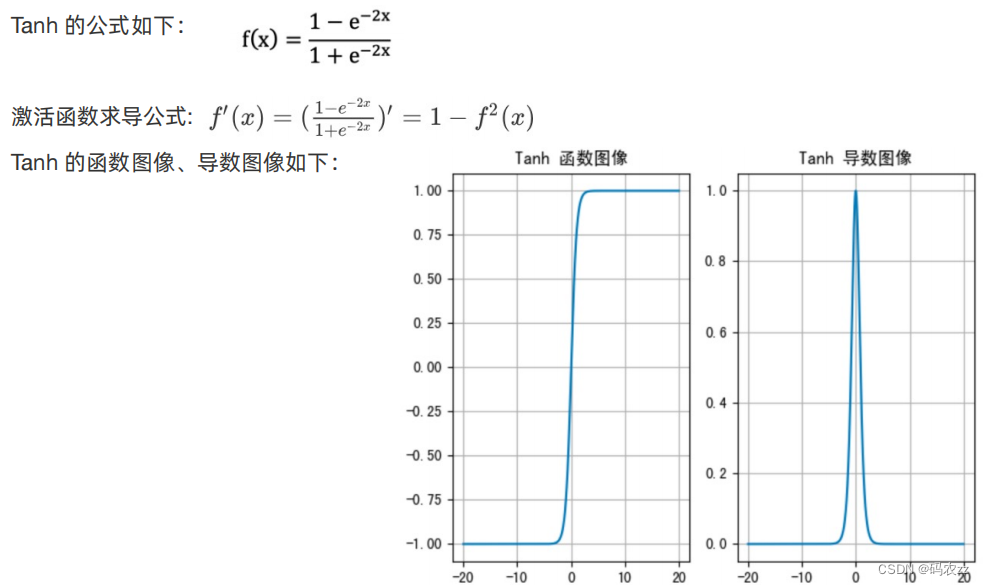
• Tanh 函数将输入映射到 (-1, 1) 之间 ,图像以 0 为中心,在 0 点对称,当输入 大概<-3 或者
>3 时将被映射为 -1 或者 1。 其导数值范围 (0, 1) ,当输入的值大概 <-3 或者 > 3 时,其导数
近似 0。
• 与 Sigmoid 相比,它是以 0 为中心的 ,且梯度相对于sigmoid大,使得其收敛速度要比
Sigmoid 快,减少迭代次数。然而,从图中可以看出,Tanh 两侧的导数也为 0,同样会造成
梯度消失。
• 若使用时可在隐藏层使用tanh函数 ,在 输出层使用sigmoid函数 。
3.relu激活函数
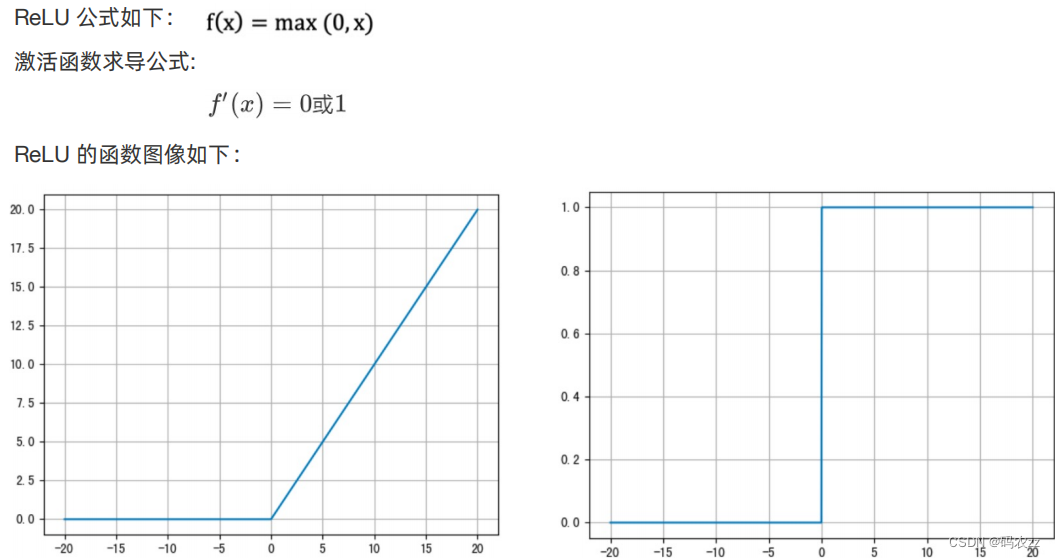
• ReLU 激活函数将小于 0 的值映射为 0,而大于 0 的值则保持不变,它更加重视正信号,而忽
略负信号,这种激活函数运算更为简单,能够提高模型的训练效率。
• 当x<0时,ReLU导数为0,而当x>0时,则不存在饱和问题。所以,ReLU 能够在x>0时保持梯
度不衰减,从而缓解梯度消失问题。然而,随着训练的推进,部分输入会落入小于0区域,导
致对应权重无法更新。这种现象被称为“神经元死亡” 。
• ReLU是目前最常用的激活函数。与sigmoid相比,RELU的优势是:
采用sigmoid函数,计算量大(指数运算),反向传播求误差梯度时,计算量相对大,而采用
Relu激活函数,整个过程的计算量节省很多。 sigmoid函数反向传播时,很容易就会出现梯度
消失的情况,从而无法完成深层网络的训练。 Relu会使一部分神经元的输出为0,这样就造成了
网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
4.SoftMax激活函数
softmax 用于 多分类 过程中,它是二分类函数 sigmoid 在多分类上的推广,目的是 将多分类的结果以概率的形式展现出来
。计算方法如下图所示:

Softmax 就是将网络输出的 logits 通过 softmax 函数,就映射成为(0,1)的值,而 这些值的累和
为1 (满足概率的性质),那么我们将它理解成概率, 选取概率最大(也就是值对应最大的)节
点 ,作为我们的 预测目标类别 。
其他常见的损失函数
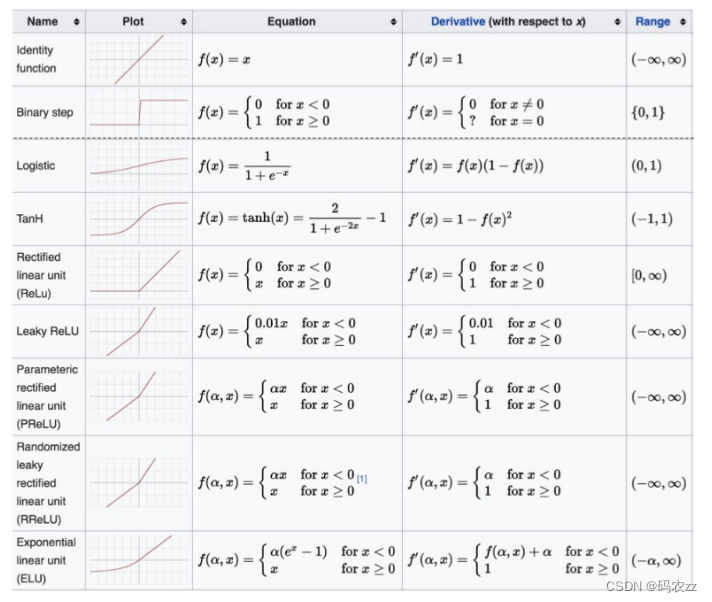
激活函数选择的方法
对于 隐藏层 :
1. 优先选择ReLU激活函数
2. 如果ReLu效果不好,那么尝试其他激活,如Leaky ReLu等。
3. 如果你使用了ReLU, 需要注意一下Dead ReLU问题, 避免出现大的梯度从而导致过多的神经元死亡。
4. 少用使用sigmoid激活函数,可以尝试使用tanh激活函数
对于 输出层 :
1. 二分类问题选择sigmoid激活函数
2. 多分类问题选择softmax激活函数
3. 回归问题选择identity激活函数
代码示例
import torch
import matplotlib.pyplot as plt# 一. 函数原图像
# 函数图像
x = torch.linspace(-20,20,1000)
# 1. 输入值x通过sigmoid函数转换成激活值y
# y = torch.sigmoid(x)# 2. 输入值x通过tanh函数转换成激活值y
# y = torch.tanh(x)# 3. 输入值x通过relu函数转换成激活值y
y = torch.relu(x)# 画图
# 创建画布和坐标轴
_,axes = plt.subplots(1,2)
axes[0].plot(x,y)
axes[0].grid()# 二. 导数图像
x = torch.linspace(-20,20,1000,requires_grad=True)# torch.sigmoid(x).sum().backward()
# torch.tanh(x).sum().backward()
torch.relu(x).sum().backward()# x.detach()输入值x的数值 x.grad 计算梯度 求导
axes[1].plot(x.detach(),x.grad)
axes[1].grid()
plt.show()参数初始化
均匀分布初始化
权重参数初始化从区间均匀随机取值。即在(-1//a,1/a)均匀分布中生成当前神经元的权重,其中d为每个神经元的输入数量
正态分布初始化
随机初始化从均值为0,标准差是1的高斯分布中取样,使用一些很小的值对参数W进行初始化
全0初始化
将神经网络中的所有权重参数初始化为 0
全1初始化.
将神经网络中的所有权重参数初始化为 1.
固定值初始化
将神经网络中的所有权重参数初始化为某个固定值
kaiming 初始化,也叫做 HE 初始化
HE 初始化分为正态分布的 HE 初始化、均匀分布的 HE 初始化
-正态化的he初始化
stddev= sqrt(2 /fan_in)
-均匀分布的he初始化
它从 [-limit,limit] 中的均匀分布中抽取样本,limit是 sqrt(6/fan_in)
它从 [-limit,limit] 中的均匀分布中抽取样本,limit是 sqrt(6/fan_in)
fan in 输入神经元的个数
xavier 初始化,也叫做 Glorot初始化
该方法也有两种,一种是正态分布的 xavier 初始化、一种是均匀分布的 xavier 初始化
-正态化的Xavier初始化
stddev=sart(2 /(fan in + fan_out))
-均匀分布的Xavier初始化
[-limit, limit]中的均匀分布中抽取样本, limit 是 sqrt(6/(fan_in + fan_out))
[-limit, limit]中的均匀分布中抽取样本, limit 是 sqrt(6/(fan_in + fan_out))
-fan_in 是输入神经元的个数,fan_out 是输出的神经元个数
代码示例
import torch
import torch.nn as nn# 1. 模型结构
layer = nn.Linear(in_features=3,out_features=5)# nn.init.uniform_(layer.weight) # 1. 均匀分布
# nn.init.normal_(layer.weight) # 2. 正态分布
# nn.init.constant_(layer.weight,5) # 3. 固定初始化
# nn.init.zeros_(layer.weight) # 4. 全0 (对bias初始化)(默认)
# nn.init.ones_(layer.weight) # 5. 全1 (对bias初始化),其他对weight# nn.init.kaiming_normal_(layer.weight) # 6. 凯明(正态分布)
# nn.init.kaiming_uniform_(layer.weight) # 凯明(均匀分布)# nn.init.xavier_normal_(layer.weight) # 7. xavier(正态分布)(默认)
nn.init.xavier_uniform_(layer.weight) # xavier(均匀分布)print(layer.weight.data)神经网络搭建和参数计算
在pytorch中定义深度神经网络其实就是层堆叠的过程,继承自nn.Module,实现两个方法:
- __init__方法中定义网络中的层结构,主要是全连接层,并进行初始化
- forward方法,在实例化模型的时候,底层会自动调用该函数。该函数中可以定义学习率,
为初始化定义的layer传入数据等。
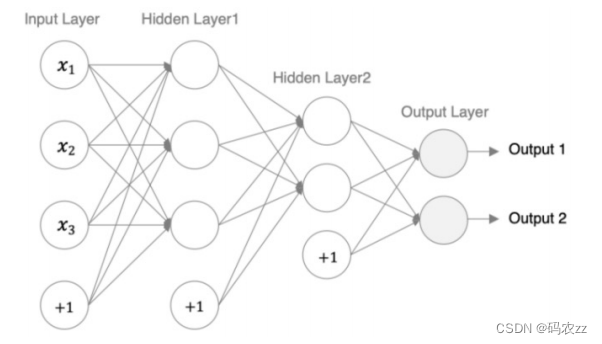
编码设计如下:
1.第1个隐藏层:权重初始化采用标准化的xavier初始化 激活函数使用sigmoid
2.第2个隐藏层:权重初始化采用标准化的He初始化激活函数采用relu3out输出层线性层 假若二分类,采用softmax做数据归一化
import torch
import torch.nn as nn
from torchsummary import summary# 构建神经网络
# 1. 定义继承自nn.Module的模型类
class model(nn.Module):# 2. 在__init__方法中定义网络中的层结构def __init__(self):# 调用父类的初始化属性值super(model,self).__init__()# 创建第一个隐藏层模型, 3个输入特征,3个输出特征self.layer1 = nn.Linear(3,3)# 初始化权重nn.init.kaiming_normal_(self.layer1.weight)# 创建第二个隐藏层模型, 3个输入特征(上一层的输出特征),2个输出特征self.layer2 = nn.Linear(3,2)# 初始化权重nn.init.kaiming_normal_(self.linear2.weight)# 创建输出层模型self.out = nn.Linear(2,2)# 3. 在forward方法中定义数据传输方式def forward(self,x):# 数据经过第一个线性层h1 = self.layer1(x)# 使用relu激活函数h1 = torch.relu(h1)# 数据经过第二个线性层h2 = self.layer2(h1)# 使用relu激活函数h2 = torch.relu(h2)# 数据经过输出层out = self.out(h2)# 使用softmax激活函数out = torch.softmax(out,dim=-1)return outif __name__ == '__main__':# 创建model对象net = model()# summary(net,input_size=(3,),batch_size=5)# 随机产生数据x = torch.randn(5,3)y = net(x)print(y.shape)# 查看模型参数for name,params in net.named_parameters():print(name)print(params)




![type may not be empty [type-empty]](https://img-blog.csdnimg.cn/direct/52a7ff7765574129847fdaea6bd1c611.png)

