分类问题经典算法 | 二分类问题 | Logistic回归：公式推导

一. Logistic回归的思想

1. 分类任务思想

分类问题通常可以分为二分类，多分类任务；而对于不同的分类任务，训练的主要目标是不变的，即找到一个分类器，这个分类器可以对新输入的数据进行判断,以确定该数据是属于哪个类别

对于分类任务，我们常设函数为 $Ax_{1}+Bx_{2}+C = 0$

下面我们先来讨论二分类任务：
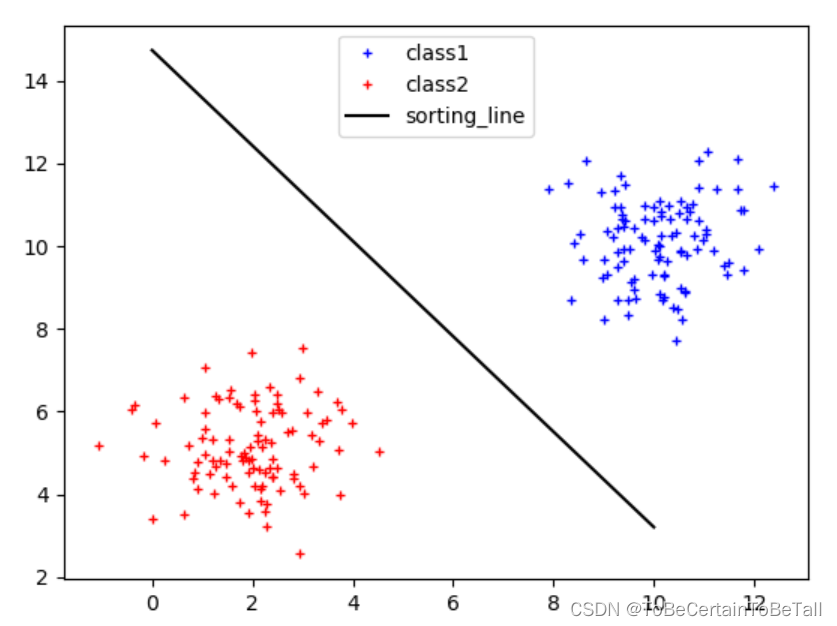
在这里插入图片描述
对于有两个特征的分类任务来说，我们的目的是寻找一条决策边界，使得这两个特征可以被区分开，如上图：

假设我们认为，决策边界为 $Ax_{1}+Bx_{2}+C = 0$
当输入一个新数据 $x_{1_{0}},x_{2_{0}})$
对于蓝色特征（右上方）就会得到：

$Ax_{1_{0}}+Bx_{2_{0}}+C > 0$ ，即正样本

对于红色特征（左下方）就会得到：

$Ax_{1_{0}}+Bx_{2_{0}}+C < 0$ ，即负样本

这里强调一点，对于分类任务：
$Ax_{1}+Bx_{2}+C = 0$ 描述的不再是特征与结果之间的关系，而是特征与特征之间的关系
我们训练的目标，从将一个特征值带入方程来求另一个特征值变成了将两个特征值带入求 $Ax_{1}+Bx_{2}+C = 0$ 的值

2. Logistic回归思想

Logistic回归算法并不满足于上述常规分类思想，而是在其基础上引入了概率的概念，即：

当输入一个新数据 $x_{1_{0}},x_{2_{0}})$

若该数据落在决策边界上：

该样本点是正样本或负样本的概率都是0.5

若该数据落在决策边界左下方，且距离决策边界越远：

该样本点为负样本的概率越大，为正样本的概率越小

若该数据落在决策边界右上方，且距离决策边界越远：

该样本点为正样本的概率越大，为负样本的概率越小

上述描述中，不难看出，Logistic回归是将距离与概率进行关联，那么具体怎样实现呢？

首先我们定义Logistic函数： $\frac{1}{1+e^{-x} }$
其中，x为样本点到决策边界的距离，即 $Ax_{1}+Bx_{2}+C = 0的值$

对于公式，简单解析下：

公式为什么会出现e？

求导方便

为什么公式中样本点到决策边界距离的计算方式与数学中不符？

数学中，点到直线的公式为 $\frac{Ax_{0}+By_{0}+C }{\sqrt{A^{2}+ B^{2}} }$ ，其中 $\sqrt{A^{2}+ B^{2}}$ 可以看作一个整数
公式中，我们求得的距离之所以没有除以 $\sqrt{A^{2}+ B^{2}}$ ，是因为每个点的相对距离是一样的

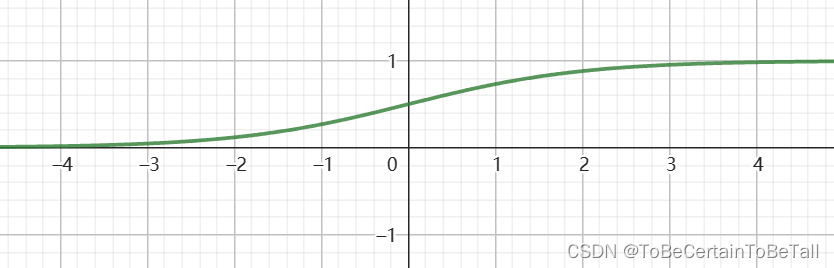
在这里插入图片描述
通过观察函数图像，我们可以看出这个函数非常符合Logistic回归思想：

	自变量x：样本点到决策边界的距离d因变量y：样本点属于正负样本的概率P当自变量为0时，P=0.5当自变量趋近-∞时，P趋近于0当自变量趋近+∞时，P趋近取1【注意】这里的距离是有正有负的

由于Logistic函数的形状类似于S，所以该函数又被称为Sigmoid函数

二. Logistic回归算法：线性可分推导

下面我们来具体聊Logistic回归算法，但在开始之前，我们先来明确分类的种类：

	对于二分类任务目标：我们需要寻找一个决策边界，从而达到将两类样本点区分的目的这里所谓的决策边界，即分类问题中进行分类决策的依据：对于二维空间，决策边界是一条直线对于三维空间，决策空间是一个平面对于多为空间，决策边界是一个超平面也就是说：当上面这些决策边界存在时，我们认为这些样本点是线性可分的当上面这些决策边界不存在时，我们认为这些样本点是线性不可分的；比如：找不到一条直线，将样本进行二分类这里补充一点：对于线性不可分的情况，我们的解决方法其实是多项式扩展

那么，接下来我们先来讨论二维空间中的线性可分问题

首先我们先用公式阐述我们的问题：

存在一条决策边界 $f(x)=\theta _{0} +\theta _{1}x_{1}+\theta _{2}x_{2} = \theta ^{T} X，f(x)为距离$

其中，令 $\frac{1}{1+e^{-x} }，g(x)为概率$
则，会得到 $h_{\theta } (x) = g(f(x))= g(\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2} )$
当确定 $\theta _{0}，\theta _{1}，\theta _{2}$ 后，就可以用 $h_{\theta } (x)$ 对新数据进行预测；需要注意的是，此时预测的是样本属于正样本的概率

结合上面对于问题的描述，我们开始对公式进行推导

假设我们采集到数据后，进行标注，得到数据集如下：

$x_{1}^{(i)}, x_{2}^{(i)}, ... , x_{N}^{(i)}, y^{(i)}$
其中，数据集的正样本标注为 $y^{(i)}=1$
其中，数据集的负样本标注为 $y^{(i)}=0$

对于线性可分问题，存在决策边界为：
$\theta _{0}+ \theta _{1}x_{1}+\theta _{2}x_{2}+ ... +\theta _{N}x_{N} = 0$

则，令
$d=\theta _{0}+ \theta _{1}x_{1}+\theta _{2}x_{2}+ ... +\theta _{N}x_{N}，这里的距离d有正负$

如果带入每个样本的特征值，就会得到每个样本点到直线的距离，即：
$\theta _{0}+ \theta _{1}x_{1}^{(i)}+\theta _{2}x_{2}^{(i)}+ ... +\theta _{N}x_{N}^{(i)}$
根据Logistic函数
$\frac{1}{1+e^{-x}}$
带入关于 $\theta$ 的函数d，我们可以得到
$h_{\theta } (x) = \frac{1}{1+e^{-d(\theta )}}$

注意：
此时计算的 $h_{\theta } (x)$ 结果是以正样本为依据，即

所计算的样本属于 正样本/正类 的概率

同理，我们就会得到计算样本属于 负样本/负类 的概率

即
$\left\{\begin{matrix}P(y=1|x;\theta ) = h_{\theta }(x) \\P(y=0|x;\theta ) = 1-h_{\theta }(x) \end{matrix}\right.$
合并后，我们会得到
$P(y|x;\theta ) = h_{\theta }(x)^{y}\left [ 1-h_{\theta }(x) \right ]^{1-y}$
这样，我们就可以得到关于 $\theta$ 的似然函数：
$L(\theta)=\prod_{i=1}^{M} h_{\theta }(x^{(i)} )^{y^{(i)} }\left [ 1-h_{\theta }(x^{(i)}) \right ]^{1-y^{(i)}}$

为了方便计算，我们对似然求对数，得到
$l(\theta )=ln\left [ L(\theta)\right ]=\sum_{i=1}^{M}\left \{y^{(i)}ln[h_{\theta}(x^{(i)} )]+(1-y^{(i)})ln[1-h_{\theta}(x^{(i)} )] \right \}$
下面，就到了我们熟悉的环节，求 $\theta$ 偏导

$\frac{\partial l(\theta )}{\partial (\theta _{j} )} =\sum_{i=1}^{M}\frac{\partial\left \{ y^{(i)}ln[h_{\theta}(x^{(i)} )]+(1-y^{(i)})ln[1-h_{\theta}(x^{(i)} )] \right \} }{\partial(\theta _{j})}$

$=\sum_{i=1}^{M}( \frac{y^{(i)}}{h_{\theta}(x^{(i)})} -\frac{1-y^{(i)}}{1-h_{\theta}(x^{(i)})})\frac{\partial(h_{\theta}(x^{(i)})) }{\partial (\theta _{j} )}$

这里我们来推导 $\frac{\partial(h_{\theta}(x^{(i)})) }{\partial (\theta _{j} )}$

其中， $h_{\theta } (x) = \frac{1}{1+e^{-d(\theta )}}$ ，又 $\frac{1}{1+e^{-x}}$

所以我们先对y进行求导

$\frac{\mathrm{d} y}{\mathrm{d} x} =\left [ -\frac{1}{(1+e^{-x} )^{2}}\ast e^{-x}\ast (-1)\right ]$

$\frac{1}{1+e^{-x}} \ast \frac{e^{-x}}{1+e^{-x}}$

$=\frac{1}{1+e^{-x}} \ast (1-\frac{1}{1+e^{-x}})$

$\ast (1-y)$

对于 $\frac{\partial(h_{\theta}(x^{(i)})) }{\partial (\theta _{j} )}$ 我们就会得到

$\frac{\partial(h_{\theta}(x^{(i)})) }{\partial (\theta _{j} )}=h_{\theta}(x^{(i)})\ast \left [ 1-h_{\theta}(x^{(i)}) \right ] \ast \frac{\partial d(\theta )}{\partial \theta _{j} }$

$\frac{\partial l(\theta )}{\partial \theta _{j} }=\sum_{i=1}^{M}( \frac{y^{(i)}}{h_{\theta}(x^{(i)})} -\frac{1-y^{(i)}}{1-h_{\theta}(x^{(i)})})\frac{\partial(h_{\theta}(x^{(i)})) }{\partial \theta _{j} }$

$=\sum_{i=1}^{M}( \frac{y^{(i)}}{h_{\theta}(x^{(i)})} -\frac{1-y^{(i)}}{1-h_{\theta}(x^{(i)})})\ast h_{\theta}(x^{(i)})\ast \left [ 1-h_{\theta}(x^{(i)}) \right ] \ast \frac{\partial d(\theta )^{(i)} }{\partial \theta _{j} }$
$=\sum_{i=1}^{M}[y^{(i)}-h_{\theta}(x^{(i)} ) ] \ast \frac{\partial d(\theta )^{(i)} }{\partial \theta _{j} }$

根据 $d(\theta )^{(i)} = \theta _{0}x_{0}^{(i)}+ \theta _{1}x_{1}^{(i)}+\theta _{2}x_{2}^{(i)}+ ... +\theta _{N}x_{N}^{(i)}$
我们可以得到
$\frac{\partial d(\theta )^{(i)} }{\partial \theta _{j} }=x_{j}^{(i)}$