剑指offer刷题记录Day2 07.数组中重复的数字 ---＞ 11.旋转数组的最小数字

名人说：莫道桑榆晚，为霞尚满天。——刘禹锡（刘梦得，诗豪）
创作者：Code_流苏(CSDN)（一个喜欢古诗词和编程的Coder😊）

目录

1、重建二叉树
①代码实现（带注释）
②补充说明（前序遍历和中序遍历重建二叉树的原理）

2、二叉树的下一个结点
①代码实现（带注释）

3、用两个栈实现队列
①代码实现（带注释）
②补充说明（栈和队列）

4、斐波那契数列
①代码实现（带注释）
②补充说明（斐波那契数列）

5、旋转数组的最小数字
①代码实现（带注释）
②补充说明（二分搜索法）

1、重建二叉树

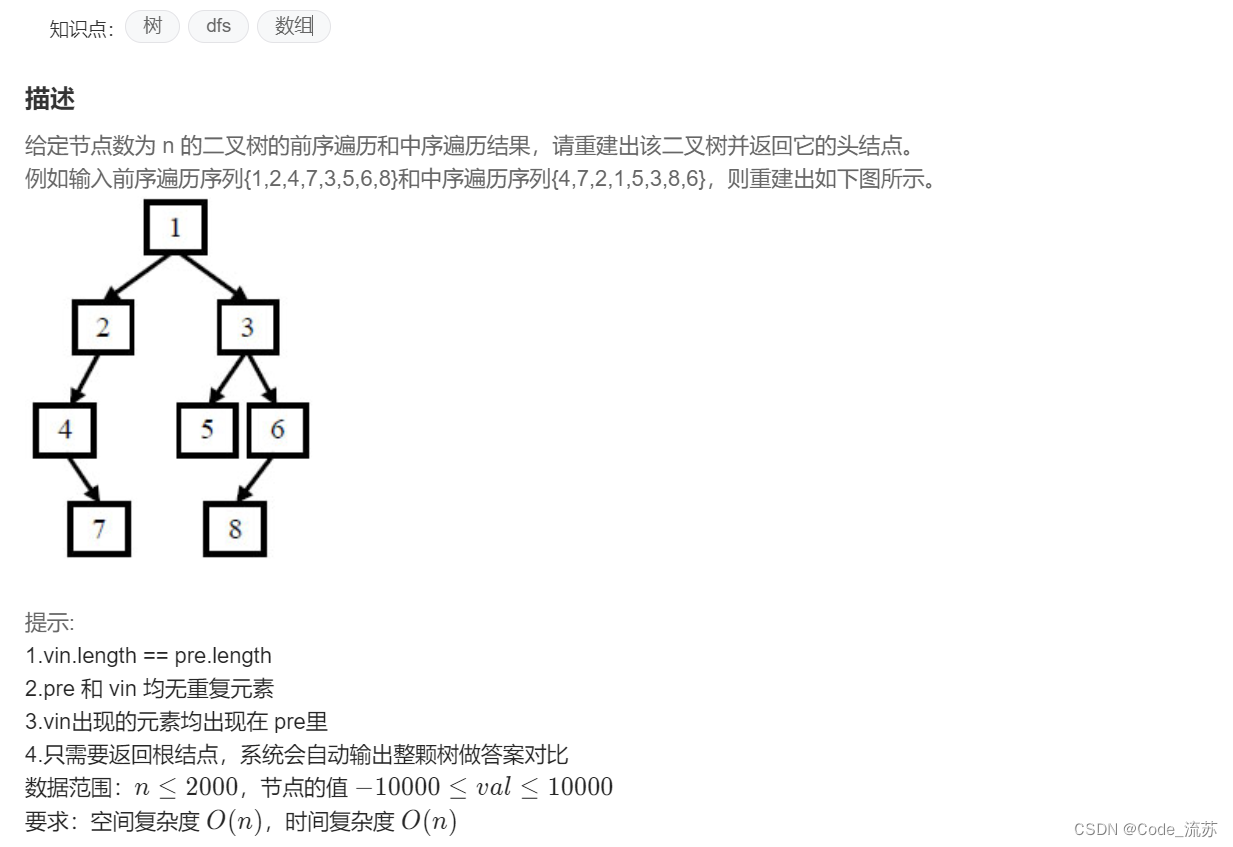
原题链接：07.重建二叉树

在这里插入图片描述

①代码实现（带注释）

#include <unordered_map>
#include <vector>
/*** struct TreeNode {*  int val;*  struct TreeNode *left;*  struct TreeNode *right;*  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* };*/
/*解题关键：前序序列中的第一个元素总是树的根。
通过这个根，我们可以在中序序列中找到根的索引位置。中序序列又总是被根索引分成两部分：左子树和右子树。
同样地，我们就能够可以确定前序序列中左右子树的边界。最后通过递归这个过程来重建整棵树即可解决问题。*/class Solution {public:unordered_map<int, int>indexMap; // 用于快速访问中序遍历中值的索引的映射TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder,int preorderStart, int preorderEnd, int inorderStart, int inorderEnd) {//若前序遍历的起始位置大于结束位置               if (preorderStart > preorderEnd) {return nullptr; //若返回 nullptr ，表示该子树不存在任何节点。}// 根据前序遍历的特点，我们可以从前序遍历获取根节点值int rootVal = preorder[preorderStart]; // 创建原二叉树的根节点TreeNode* root = new TreeNode(rootVal); // 在中序遍历中找到根的索引下标int rootIndexInInorder = indexMap[rootVal]; // leftElements:左子树中的元素数量int leftElements = rootIndexInInorder - inorderStart;// 递归构建左子树root->left = buildTree(preorder, inorder, preorderStart + 1,preorderStart + leftElements, inorderStart, rootIndexInInorder - 1);// 递归构建右子树root->right = buildTree(preorder, inorder, preorderStart + leftElements + 1,preorderEnd, rootIndexInInorder + 1, inorderEnd);//返回每次所构建子树的根节点return root;}TreeNode* reConstructBinaryTree(vector<int>& preOrder, vector<int>& vinOrder) {int n = preOrder.size();// 填充indexMap以便快速访问中序遍历中的索引/*在重建二叉树的过程中，需要频繁地找到前序遍历中的根节点在中序遍历序列中的位置，这样才能确定左右子树的范围，因此此处使用了映射。如果不使用映射，每次查找都可能需要遍历整个中序遍历序列来找到根节点的位置*/for (int i = 0; i < n; i++) {indexMap[vinOrder[i]] = i;}return buildTree(preOrder, vinOrder, 0, n - 1, 0, n - 1);}
};

在这里插入图片描述

②补充说明（前序遍历和中序遍历重建二叉树的原理）

该题根据前序遍历和中序遍历重建二叉树的原理是什么？

构建二叉树的原理依赖于前序遍历和中序遍历的特性来确定树的结构。前序遍历的顺序是根左右。中序遍历的顺序是左根右。

根据前序遍历和中序遍历构建二叉树的步骤：

确定根节点：在前序遍历中，序列的第一个元素总是树的根节点。
划分左右子树：在中序遍历中，根节点将序列分为两部分，左边是树的左子树，右边是树的右子树。
递归构建：利用上一步得到的左右子树的中序遍历序列，和从前序遍历序列中提取相应的左右子树序列，递归地重复上述过程构建整棵树。

例如，假设有一棵树的前序遍历序列是 $[\text{A}, \text{B}, \text{D}, \text{E}, \text{C}, \text{F}]$ ，中序遍历序列是 $[\text{D}, \text{B}, \text{E}, \text{A}, \text{C}, \text{F}]$ ：

前序遍历的第一个元素是 $A$ ，所以 $A$ 是根节点。
在中序遍历中， $A$ 前面的 $[\text{D}, \text{B}, \text{E}]$ 是左子树的中序遍历序列， $A$ 后面的 $[\text{C}, \text{F}]$ 是右子树的中序遍历序列。
递归构建左子树和右子树。
- 对于左子树，前序遍历序列变为 $[\text{B}, \text{D}, \text{E}]$ ，中序遍历序列是 $[\text{D}, \text{B}, \text{E}]$ 。重复上述步骤，可以构建出左子树。
- 对于右子树，前序遍历序列是 $[\text{C}, \text{F}]$ ，中序遍历序列是 $[\text{C}, \text{F}]$ 。重复上述步骤，可以构建出右子树。

通过这种方式，我们就可以准确地重建原始的二叉树结构了。

2、二叉树的下一个结点

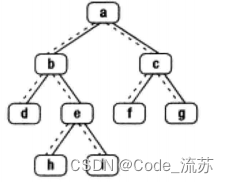
原题链接：08.二叉树的下一个结点

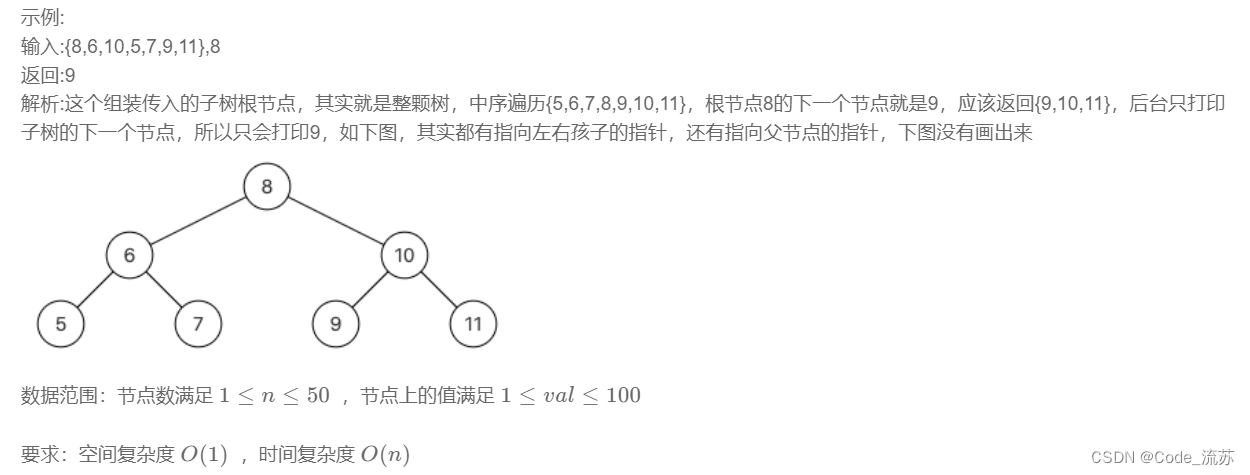
在这里插入图片描述

①代码实现（带注释）

/*
struct TreeLinkNode {int val;struct TreeLinkNode *left;struct TreeLinkNode *right;struct TreeLinkNode *next;TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL) {}
};
*/
class Solution {public:// 定义树节点指针向量nodes 用于存储中序遍历所有节点指针vector<TreeLinkNode*> nodes;// 获取给定节点的下一个节点TreeLinkNode* GetNext(TreeLinkNode* pNode) {TreeLinkNode* root = pNode;// 循环遍历找到根节点while (root->next) root = root->next;// 对树进行中序遍历，并将节点指针存储在nodes向量中InOrder(root); int n = nodes.size(); // 获取遍历后得到的节点总数// 遍历节点，查找给定节点的下一个节点for (int i = 0; i < n - 1; i++) {TreeLinkNode* cur = nodes[i];// 如果当前节点是给定节点if (pNode == cur) { // 则返回下一个节点return nodes[i +1]; }}// 若给定节点没有下一个节点，则返回NULLreturn NULL; }// 中序遍历二叉树void InOrder(TreeLinkNode* root) {if (root == NULL) return;InOrder(root->left); // 遍历左子树//push_back函数可以在Vector向量最后添加一个元素（括号中的参数为要插入的值）nodes.push_back(root); // 访问当前节点InOrder(root->right); // 遍历右子树}
};

在这里插入图片描述

3、用两个栈实现队列

原题链接：09.用两个栈实现队列

在这里插入图片描述

①代码实现（带注释）

class Solution
{
public://使用两个栈实现队列的push操作void push(int node) {stack1.push(node); //直接将元素压入stack1}//使用两个栈实现队列的pop操作int pop() {//如果stack2为空，则将stack1中的所有元素转移到stack2中if (stack2.empty()) {while (!stack1.empty()) {//将stack1的栈顶元素压入stack2stack2.push(stack1.top());//删除stack1的栈顶元素stack1.pop();}}//如果stack2不为空，则直接从stack2中弹出栈顶元素，即队头元素//获取stack2的栈顶元素int head = stack2.top(); //删除stack2的栈顶元素stack2.pop();//返回队头元素return head;}private:stack<int> stack1;//栈1用于插入操作stack<int> stack2;//栈2用于删除操作
};

在这里插入图片描述

②补充说明（栈和队列）

栈（Stack）和队列（Queue）是两种基本的数据结构，它们在处理数据的方式上有着本质的区别：

栈是一种后进先出的数据结构。
最后添加进栈的元素将是第一个被移除的。想象一下一叠盘子，你只能从顶部添加或移除盘子。常见的操作包括“push”（添加一个元素到栈顶）和“pop”（移除栈顶元素）。
队列是一种先进先出的数据结构。
第一个添加进队列的元素将是第一个被移除的。可以想象成在银行排队，新来的顾客排在队伍的末尾，而服务员从队伍的前端开始服务顾客。常见的操作包括“enqueue”（将一个元素添加到队列末尾）和“dequeue”（移除队列前端的元素）。

4、斐波那契数列

原题链接：10. 斐波那契数列
在这里插入图片描述

①代码实现（带注释）

class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** * @param n int整型 * @return int整型*/int Fibonacci(int n) {//处理边界情况if(n <= 1)return n;//初始化前两个斐波那契数	int a=0,b=1;//计算第n项for(int i = 2; i <= n; i++){//更新斐波那契数到第n项int next = a+b;a = b;b = next;}//第n项的斐波那契数列return b;}
};

在这里插入图片描述

②补充说明（斐波那契数列）

斐波那契数列是一种在数学和计算机科学中广泛应用的数列。它由以下递归关系定义：每个数是前两个数的和，其最初两个数通常定义为 $F (0) = 0, F (1) = 1$ 。因此，斐波那契数列的开始部分是：

$\ldots$

形式上，斐波那契数列可以用数学公式表示为：

$F (n) = F (n - 1) + F (n - 2)$

其中， $\geq 2$ 且 $F (0) = 0$ , $F (1) = 1$ 。

特点：除了最开始的两个数字外，每个数字都是其前两个数字的和。

5、旋转数组的最小数字

原题链接：11. 旋转数组的最小数字

在这里插入图片描述

①代码实现（带注释）

class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** * @param nums int整型vector * @return int整型*//*由于数组原本是非降序排列的，旋转后，数组被分成两个非降序的子数组。最小值是这两个子数组的分界点。 因此我们可以使用二分搜索法/折半查找法来优化搜索过程，这样时间复杂度就是O(logn)。*/ int minNumberInRotateArray(vector<int>& nums) {//如果数组为空，返回-1if(nums.empty()) return -1; //定义左侧left位置为0int left = 0;//右侧right位置为n-1int right = nums.size() - 1;//如果旋转数组没有旋转（例如[1,2,3,4,5]变成[1,2,3,4,5]），直接返回第一个元素if(nums[left] < nums[right]){return nums[left];}//二分查找while (left < right) {int mid = left + (right - left) / 2;if(nums[mid] > nums[right]){//[mid+1,right]区间left = mid + 1;}else if (nums[mid] < nums[right]) {//[left,mid]区间right = mid;}else {//当中间值和右边值相等时，缩小范围right--;}}//循环结束，此时left == right，指向的就是数组中的最小值return nums[left];}
};

在这里插入图片描述

②补充说明（二分搜索法）

二分搜索法（Binary Search）是一种在有序数组中查找特定元素的高效算法。

原理：将待搜索的数组分成两半，然后根据中间元素与目标值的比较结果来确定下一步搜索的区域，从而逐步缩小搜索范围，直到找到目标值或确定目标值不存在。

二分搜索的基本步骤如下：

确定搜索区间：初始搜索区间为整个数组。
找到中间元素：计算搜索区间的中点位置，取出中间元素进行比较。
比较中间元素与目标值：
- 如果中间元素正好等于目标值，则搜索成功。
- 如果中间元素小于目标值，则将搜索区间调整为中间元素右侧的子区间，继续搜索。
- 如果中间元素大于目标值，则将搜索区间调整为中间元素左侧的子区间，继续搜索。
重复步骤2和3，直到找到目标值或搜索区间为空（表示目标值不存在于数组中）。

二分搜索的效率较高，其时间复杂度为 $O(\log n)$ ，其中 $n$ 是数组的长度。因此本题采用二分搜索法，可以帮助我们在查找数据时节省大量的时间。