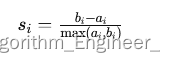目录
🧂1.动态规划思想
🌭2.背包问题思路分析
🍿3.代码实现
1.动态规划思想
- 将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法
- 适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的
2.背包问题思路分析
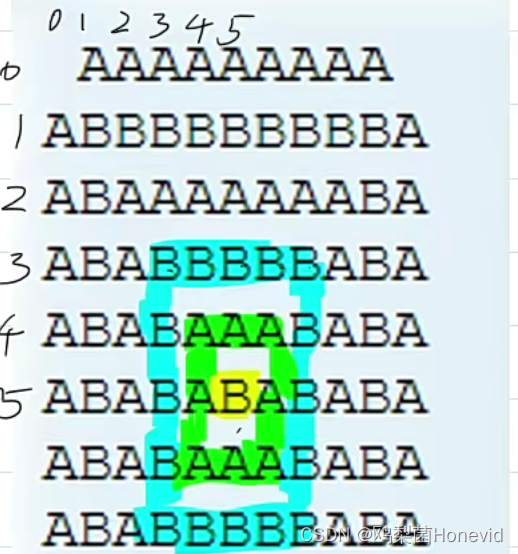
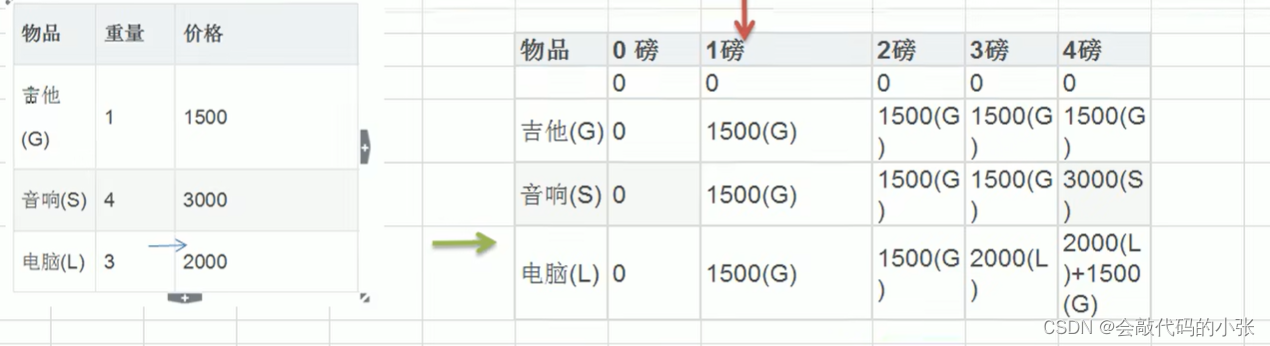
每次遍历到的第i个物品,根据w【i】和v【i】来确定是否需要将该物品放入背包中。即对于给定的n个物品,设v[i]、w[i]分别为第i个物品的价值和重量, C为背包的容量。再令v[i][j]表示在前i个物品中能够装入容量为j的背包中的最大价值。则我们有下面的结果:
- 1.v[0][j]=v[i][0]=0
- 2.w[i]>j时,v[i][j]=v[i-1][j]
- 3.j>w[i]时,v[i][j]=max{v[i-1][j],v[i]+v[i-1][j-w[i]]}
- v[i-1][j]:上一个单元格的装入的最大值
- v[i]:当前商品的价值
- v[i-1][j-w[i]]:装入i-1商品,到剩余空间j-w[i]的最大值
3.代码实现
public class KnapsackProblem {public static void main(String[] args) {//商品重量int[] w = {1, 4, 3};//商品价值int[] val = {1500, 3000, 2000};//背包容量int m = 4;//商品个数int n = val.length;//表示前n个物品中,能够装入背包容量为m的最大价值int[][] v = new int[n + 1][m + 1];//方便定位int[][] path = new int[n + 1][m + 1];//第一列制0for (int i = 0; i < v.length; i++) {v[i][0] = 0;}//第一行制0for (int i = 0; i < v[0].length; i++) {v[0][i] = 0;}/*** 根据公式,动态规划处理*/for (int i = 1; i < v.length; i++) {for (int j = 1; j < v[0].length; j++) {if (w[i - 1] > j) {v[i][j] = v[i - 1][j];} else {if (v[i - 1][j] < val[i - 1] + v[i - 1][j - w[i - 1]]) {v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];//记录path[i][j] = 1;} else {v[i][j] = v[i - 1][j];}}}}//查看所有for (int i = 0; i < v.length; i++) {for (int j = 0; j < v[0].length; j++) {System.out.print(v[i][j] + " ");}System.out.println();}//定位商品int i = path.length-1;int j = path[0].length-1;while (i > 0 && j > 0) {if (path[i][j] == 1) {System.out.println("第"+i+"个商品放入到背包");j -= w[i - 1];}i--;}}
}