排序——归并排序

归并排序和快排一样，都是一种利用二叉树分治思想实现的排序。同时归并排序也和快排一样有递归归并排序和非递归归并排序两种。本节主要复习归并排序，并且两种实现方式都会复习到。

递归归并

要实现递归归并排序的代码。我们首先需要理解递归归并排序的思想。递归归并的过程如下：

假如有一个数组

int a[10] = { 9, 0, 7, 5, 4, 3, 1, 2, 8, 6 };
int sz = sizeof(a) / sizeof(a[0]);

要对这个数组进行排序。

那么利用归并的分治思想，就是先将数据进行如图划分。

图中每个子节点都标识范围内的数据。比如9 0 7就表示0倒2这个区间内的三个数据。然后进行后序归并。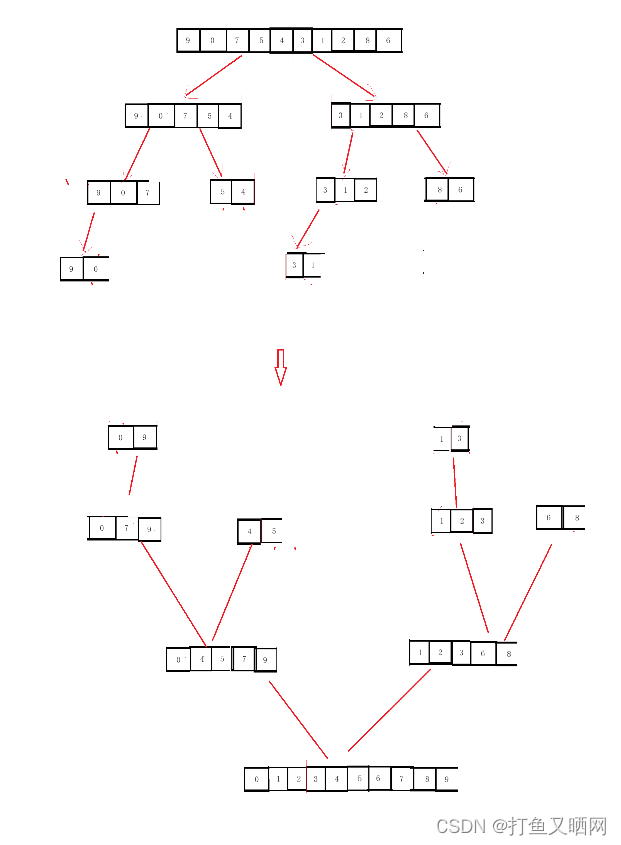

代码实现如下

首先创建一个子函数，方便递归, _MergeSort就是我们要实现的归并排序过程

void MergeSort(int* a, int sz) 
{int* tmp = (int*)malloc(sizeof(int) * sz);//_MergeSort(a, 0, sz - 1, tmp);free(tmp);
}


//归并排序递归版本
void _MergeSort(int* a, int left, int right, int* tmp) 
{if (left >= right)//如果区间不存在或者只剩下一个节点， 直接返回。 {return;}//int mid = (left + right) / 2;//让区间中分_MergeSort(a, left, mid, tmp);//从左边开始归并。 两两一组进行归并。_MergeSort(a, mid + 1, right, tmp);//两俩个一组//后续归并。所以先递归再进行归并int begin1 = left;//对中分点的左右两个区间进行归并。 begin1 为第一个区间左边int end1 = mid;//end1为左区间右边。int begin2 = mid + 1;//begin2为右区间左边int end2 = right;//end2为右区间右边int j = left;//让j从左区间左边开始控制， j是控制tmp拷贝数组的拷贝。 在一块区间进行归并， 就应该将这块区间的数据拷贝到tmp的对应区间上while (begin1 <= end1 && begin2 <= end2) //只要两个区间都没有超出去， 就进行判断，那个数据小， 拷贝哪个。{if (a[begin1] < a[begin2]) {tmp[j++] = a[begin1++];}else {tmp[j++] = a[begin2++];}}while (begin1 <= end1) //如果左区间还没完， 就继续拷贝{tmp[j++] = a[begin1++];}while (begin2 <= end2) //如果右区间还没完， 就继续拷贝{tmp[j++] = a[begin2++];}memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));}

非递归归并

进行非递归归并，归并的过程也是一种分治，不过利用了一个gap值控制每次归并的分治区间大小。直接上代码

//归并非递归
void MergeSortRno(int* a, int sz) 
{int* tmp = (int*)malloc(sizeof(int) * sz);//int gap = 1;while (gap < sz) {gap *= 2;}
}
着段代码的意思是，从区间为1开始，归并之后。区间乘以二。然后再进行归并。然后再乘以二，再进行归并。最后一次归并可能很巧合gap就是sz / 2，这个时候不需要进行其他操作。但是如果最后一次归并gap 比 sz / 2大的话。那么就需要额外的操作。这个问题会放到后面说，这里先不讨论。先将归并的内容实现。

//归并非递归
void MergeSortRno(int* a, int sz) 
{int* tmp = (int*)malloc(sizeof(int) * sz);//int gap = 1;while (gap < sz) {for (int i = 0; i < sz; i += 2 * gap) {}gap *= 2;}
}
归并的时候每gap是一个区间，每两个区间进行归并。当gap很小的时候，很显然这个数组一定不是只有一两个区间。这些区间进行归并的时候，应该将所有的区间两两归并。从下标为0，向后依次进行。

这里for循环就是来完成这个操作的，如图为gap为1的时候进行的归并，每两个区间进行归并，一共五组，从左到右依次进行：

然后具体的递归过程就和递归归并的归并过程大概是一样的了。
//归并非递归
void MergeSortRno(int* a, int sz) 
{int* tmp = (int*)malloc(sizeof(int) * sz);//int gap = 1;while (gap < sz) {for (int i = 0; i < sz; i += 2 * gap) {//归并过程int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;if (end1 > sz || begin2 > sz) {break;}if (end2 > sz) {end2 = sz - 1;}int j = i;while (begin1 <= end1 && begin2 <= end2) {if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else {tmp[j++] = a[begin2++];}}while (begin1 <= end1) {tmp[j++] = a[begin1++];}while (begin2 <= end2) {tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));//请注意这里}gap *= 2;}
}
这里之所以说是大概，就是因为这里有个超出范围的坑。我们进行非递归归并的过程过程中可能遇到这种情况。

就比如我们这个十个大小的数组，当gap为2的时候范围就出问题了。如图：

当gap为二的时候，第一组进行归并的是0-1区间和2-3区间归并。第二组区间分别是4-5和6-7归并。第三组本来应该是8-9和10-11，但是10-11不在数组里面。我们是没有访问权限的。

所以这就出问题了。那么解决问题的方式就是对着种越界情况进行判断。

我们分析这种越界情况有几种？

第一种：第一个区间的右区间超出范围，这种显然不成立。

第二种：第二个区间的左区间超出范围，当第一个区间的右区间超出时这种就一定成立。

第三种：第二个区间的左区间没有超范围，也就是第一种和第二种情况都不符合的情况下右区间超出了范围。

那么解决方法就是这几行代码：
	if (end1 > sz || begin2 > sz) {break;}if (end2 > sz) {end2 = sz - 1;}
首先第一个if的意思就是第一种情况或者第二种情况。这个时候break就行了。最后一组的第二个区间不存在，不需要进行归并，直接跳出循环就行了。

第二个if就是在第一种情况合第二种情况都不符合的情况下可能符合。这个时候最后一组的第二个区间内有数据，但是和其他的区间数据个数不同，虽然不同，但它也是可以进行归并的。所以我们只要修改右区间的范围就行了。