刷题日记:面试经典 150 题 DAY3
- 274. H 指数
- 238. 除自身以外数组的乘积
- 380. O(1) 时间插入、删除和获取随机元素
- 134. 加油站
- 135. 分发糖果
274. H 指数
原题链接 274. H 指数
重要的是都明白H指数到底是是个啥。注意到如果将引用数从大到小排序,则对于下标i有 引用数 ≥ c i t a t i o n [ i ] 的论文有 i + 1 篇 引用数\geq citation[i]的论文有i+1篇 引用数≥citation[i]的论文有i+1篇,注意到此时引用数递减而文章数量递增,所求H指数就是求一个交点。
class Solution {
public:int hIndex(vector<int>& citations) {sort(citations.begin(), citations.end(),greater<int>());int i;for(i = 0;i<citations.size() && citations[i]>=(i+1);i++);return i;}
};
其实时间复杂度为 O ( N ) O(N) O(N)的算法更加符合直觉。我们创建一个新的数组count来记录,count[i]中存储引用数为i的文章有几篇,这里面重要的一步是将引用数大于等于n的篇数存储到count[n] 之中,这是因为对于本题来说,h指数不可能大于n,所以大于n篇数的分别计数就没有意义(该思想经常出现)
class Solution {
public:int hIndex(vector<int>& citations) {int n = citations.size();int count[n+1];memset(count,0,sizeof(count));for(int cite:citations) {if(cite >= n) {count[n]++;} else {count[cite]++;}}int sum = 0,i = 0;for(i = n; i>=0;i--) {sum += count[i];if(sum >= i) {break;}}return i;}
};
238. 除自身以外数组的乘积
原题链接 238. 除自身以外数组的乘积
题很简单,只需要注意到要处理0,可以分类讨论
- 不存在0,则只需要算出整体乘积,然后除以当前数字
- 存在一个0,则除了这个0外剩下位置都是0,该位置是所有其它数乘积
- 存在两个及以上0,则全是0
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int count_0 = 0;int len = nums.size();int total = 1;for(int num:nums) {if(num == 0) count_0++;else total*=num;}vector<int> result(len,0);if(count_0 >= 2) {return result;}if(count_0 == 1) {for(int i = 0;i < len;i++) {if(nums[i] == 0) {result[i] = total;}}return result;}for(int i = 0;i < len;i++) {result[i] = total/nums[i];}return result;}
};
380. O(1) 时间插入、删除和获取随机元素
原题链接 380. O(1) 时间插入、删除和获取随机元素
数据结构设计题,之前没试过这类题,自己做想到要用哈希(废话),但是感觉脑子不够用,遂去狠狠的学习了【宫水三叶】数据结构运用题
class RandomizedSet {
private:unordered_map<int,int> hashmap;int nums[200010];int idx;
public:RandomizedSet() {srand((unsigned)time(NULL));idx = -1;}bool insert(int val) {if(hashmap.count(val) > 0) {return false;}nums[++idx] = val;hashmap[val] = idx;return true;}bool remove(int val) {if(hashmap.count(val) == 0) {return false;}int tail = nums[idx];int rm_idx = hashmap[val];swap(nums[rm_idx],nums[idx]);hashmap.erase(val);if(val != tail) hashmap[tail] = rm_idx;idx--;return true;}int getRandom() {int random_i = rand() % (idx+1);return nums[random_i];}
};/*** Your RandomizedSet object will be instantiated and called as such:* RandomizedSet* obj = new RandomizedSet();* bool param_1 = obj->insert(val);* bool param_2 = obj->remove(val);* int param_3 = obj->getRandom();*/
结构:
- 一个定长数组用于存储元素,维护一个idx,表示在数组的
[0...idx]中存储着元素 - 一个哈希表,存储键值对
(val,idx),即元素和其所在的下标
插入
- 直接向哈希表和数组的末尾插入
删除
- 对哈希表的操作:直接删除其键值对
- 对数组的操作:将要删除的量交换到最后,然后让idx减去1(经常用到),此时需要再更新哈希表。将key为原数组尾的值改成交换后的下标
134. 加油站
原题链接 134. 加油站
朴素的想法是,我只需要模拟开车的过程,并一个一个尝试哪一个加油站可以作为起点就可以。但是这个方法复杂度有 O ( N 2 ) O(N^2) O(N2)
能在 O ( N ) O(N) O(N)内做出来的方法基于以下重要观察:
- 如果从 i i i出发能到达 j j j而无法到达 j + 1 j+1 j+1,则从任何的 k ∈ [ i , j ] k \in[i,j] k∈[i,j]出发都不可能到达 j + 1 j+1 j+1,也就是任何的 k ∈ [ i , j ] k \in [i,j] k∈[i,j]都不可能作为起点,所以我们直接从 j + 1 j+1 j+1开始检查即可
- 这是因为到达 k k k时汽车至少有非负的汽油,一定不低于从 k k k出发的汽油
所以我们能在每个元素至多被遍历两遍内获得答案
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int len = gas.size();int i = 0;while(i < len) {int cargas = 0;int cnt;for(cnt = 0;cnt < len;cnt++) {int j = (i+cnt)%len;cargas += gas[j]-cost[j];if(cargas < 0) {break;}}if(cnt == len) {return i;} else {i += cnt+1;}}return -1;}
};
135. 分发糖果
原题链接 135. 分发糖果
第一遍做想到一个比较符合直觉的想法:考虑两种打分的分布,分别是:递增,递减
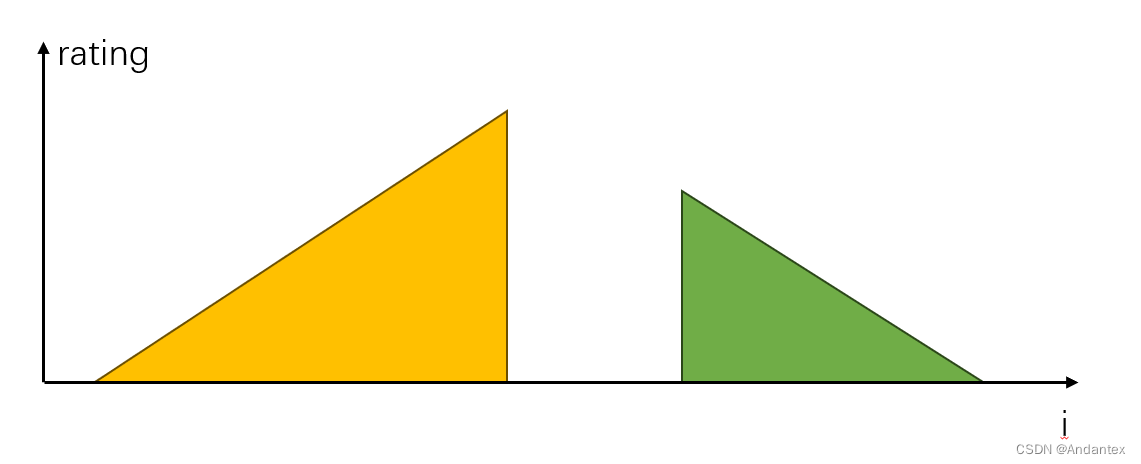
这样分糖果的策略很简单,就是在单调列中,这个孩子是打分第几低,我就给他几个糖果
实际打分的分布可以看作是多个递增递减列的组合
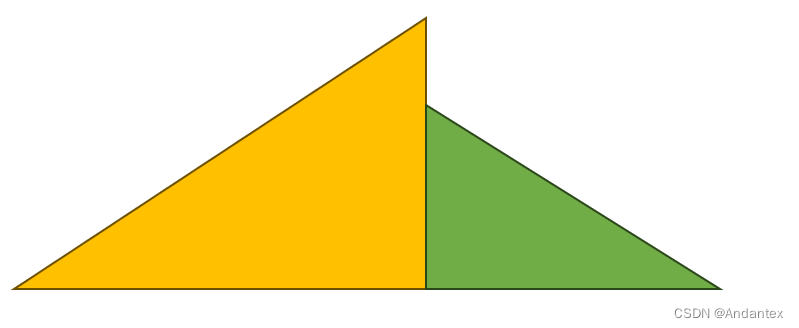
此时仅需要考虑中间那个孩子需要多少糖果即可,很简单能想到应该是max(left,right)
最后写成代码:
class Solution {
public:int candy(vector<int>& ratings) {int len = ratings.size();vector<int> uplift(len,0);vector<int> downlift(len,0);int cd = 0;for(int i = 1;i < len;i++){if(ratings[i]>ratings[i-1]) {cd++;} else {cd = 0;}uplift[i] = cd;}cd = 0;for(int i = len-2;i >= 0;i--){if(ratings[i]>ratings[i+1]) {cd++;} else {cd = 0;}downlift[i] = cd;}cd = len;for(int i = 0;i < len;i++){cd += max(uplift[i],downlift[i]);}return cd;}
};