基于STM32F4的FFT（快速傅里叶变换）求信号幅值，频率，相位差

一。FFT原理介绍

快速傅里叶变换（Fast Fourier Transform，FFT）是一种用于高效计算傅里叶变换的算法。傅里叶变换是一种信号处理技术，将信号从时域（时间域）转换到频域（频率域），它可以将一个信号分解成不同频率的成分，因此在信号处理、通信、图像处理等领域有着广泛的应用。FFT 算法的核心思想是将一个长度为 N 的离散序列的 DFT（离散傅里叶变换）分解成若干个长度为 N/2 的子问题。通过递归地将原问题分解成规模更小的子问题，然后再合并子问题的结果，最终得到整个序列的 DFT。FFT 算法的时间复杂度为 O(N log N)，相比传统的直接计算 DFT 的算法（时间复杂度为 O(N^2)），FFT 在处理大规模数据时具有明显的效率优势。这使得 FFT 成为了数字信号处理、频谱分析等领域中的核心算法之一。FFT 算法的原理可以用到多种变种上，如 Cooley-Tukey FFT 算法是最著名的一种，它利用了傅里叶变换的周期性和对称性，将 DFT 分解成长度为 N/2 的子问题。通过反复应用这种分解和合并的思想，最终实现了快速的傅里叶变换。除了 Cooley-Tukey FFT 算法外，还有其他的 FFT 算法，例如基于拉德姆赫-哈根（Rader）方法的算法，用于特定长度的序列，以及 Bluestein FFT 算法，用于非 2 的幂次长度的序列等等。这些算法在实际应用中根据不同的场景和需求选择使用。有疑问可联系微信：wpt666aaa qq:2036795517 交流。

二。装置的介绍

犹记得那天风很大，头发被吹掉了几根，依旧倔强的敲出了几百行代码，为此世界第一伟大的FFT代码，被我用STM32F4给实现了，下面允许我介绍一下用法以便各位仁兄参考：

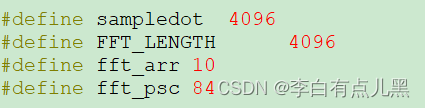
采样点数是4096（自己可以调整）
采样频率自己根据自动重装载值fft_arr和fft_psc计算和调整
在这里插入图片描述

信号的两个输入通道（可由信号发生器产生从而进行测试，也可直接接入自己想要测量的信号）
PA6对应的adc1通道一，PA5对应的adc2通道2
在这里插入图片描述

关键变量直流分量频率幅度相位（难点在于对3个变量的精确的求解）
在这里插入图片描述

变量的串口端显示：（当然也可接入OLED屏幕来显示我们获取到的参数，我这里OLED 屏幕是用的4针，IIC协议）
在这里插入图片描述

核心算法部分，我也是似懂非懂，建议在复盘一下数学
在这里插入图片描述

三。结果展示

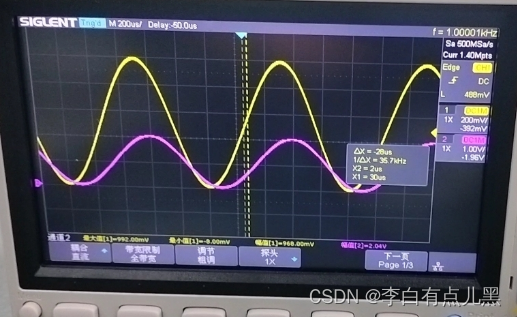
我本人是用的信号发生器来验证的我的代码的准确性，其中两个信号的相位差我是可以控制的，我这里设置的是30度，频率设置记得一定要一致，幅值设置记得不要超过3.3V不然会烧掉开发板。
1.这是我用来测试的两个信号
在这里插入图片描述
2.这是我用的开发板（这里如果是做课设或者毕设的，建议不要买整个板子，只需要在淘宝收索STM32F407ZGT6把这个芯片买下来即可，剩余的可联系我帮你解决，微xin: wpt666aaa qq: 2036795517）

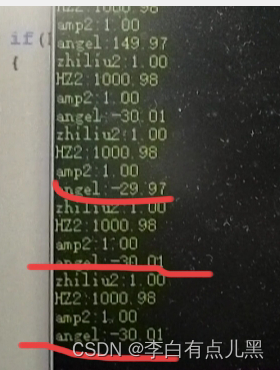
3.可以看到测试结果比较精准：幅值，频率，直流分量，相位差均正确
在这里插入图片描述
4.占用内存展示，STM32F407ZGT6这个芯片是完全够用了

四。最后的最后

如果各位仁兄有什么问题可直接加我联系方式微信：wpt666aaa qq:2036795517.我是只发布高质量文章的技术博主：李白有点儿黑。另外，我在B站针对于此项目整了一个视频演示帮助大家参考，链接我就放在下方了
https://www.bilibili.com/video/BV1yx421Z7Wm/?vd_source=f367fce8d1af1d597a20d607088ec8bb#reply210947598704
在这里插入图片描述