一、约束规则
约束规则用于指定要素上允许的属性配置和一般关系。
与计算规则不同,约束规则不用于填充属性,而是用于确保要素满足特定条件。
简单理解,约束规则就是约束你的编辑操作在什么情况下可执行。
如果出现不符合规则的操作,就会报错,操作中断。
1、禁止删除特定的要素
如果你想控制你的编辑操作,避免某些图斑被误删除,就可以设定这样的规则。
比如在用地图斑中,我不想【耕地】被删除,可以将触发器选择为【删除】,在表达式中输入:
if ($feature.DLMC != "耕地")
{return true;
}删除的图斑如果【DLMC】的字段值为“耕地”,就会弹出错误。

2、限制编辑内容在特定范围内
比如数据库里有2个图层,(因为代码要通过数据库这一共同联系作为媒介,所以2个图层一定要在同一数据库内)。
限制设施点必须在用地范围的边界内。
将触发器选择为【插入、更新】,在表达式中输入:
// 从同一个数据库里找到“用地范围”
var fw = FeatureSetByName($datastore, "用地范围", null, false);
// 用地范围和当前编辑的设施点相交,如果结果不为空(数量大于0),就给予通过。
// 否则就报错
return Count(Intersects(fw, Geometry($feature))) > 0新创建的设施点如果在用地范围外,就会弹出错误。
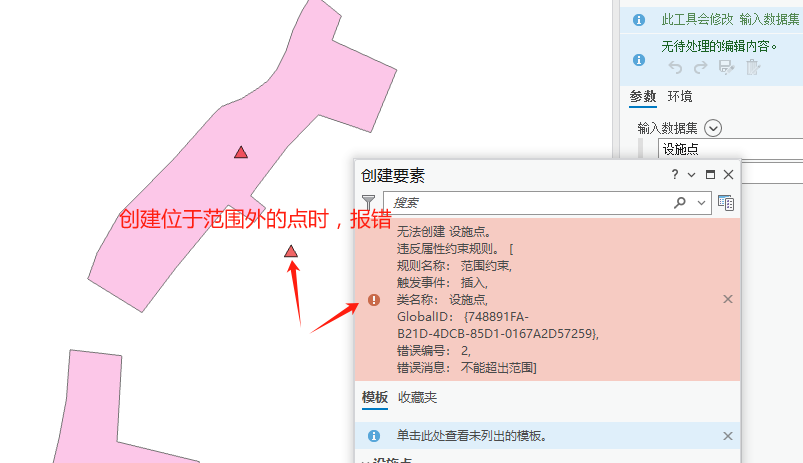
3、禁止碎面
可以通过限制图斑的面积来禁止碎面的产生。
将触发器选择为【插入、更新】,在表达式中输入:
// 获取图斑面积
var mj = area(geometry($feature));
// 如果面积大于1平方米,就通过
if(mj>1)return true新创建或修改的图斑面积小于1平方米,就会弹出错误:
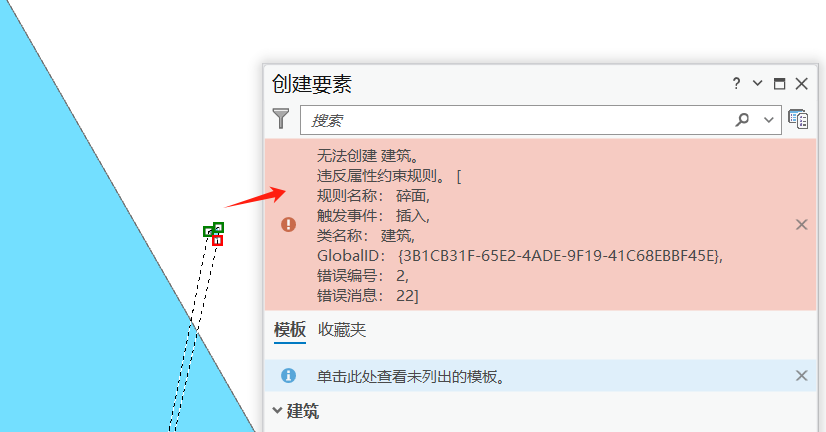
4、禁止超短线
通过计算相邻点之间的距离,可以禁止画出超短线。
将触发器选择为【插入、更新】,在表达式中输入:
// 获取环
var rings = geometry($feature)["rings"]
// 逐环处理
for(var i in rings){// 环内每个点处理for(var j=0; j < count(rings[i])-1; j++) {// 算距离 var dis = Distance(rings[i][j],rings[i][j+1],'meters')if(dis>1)return true}
}创建或修改的时候,如果边界点之间的距离小于1米,就会弹出错误:
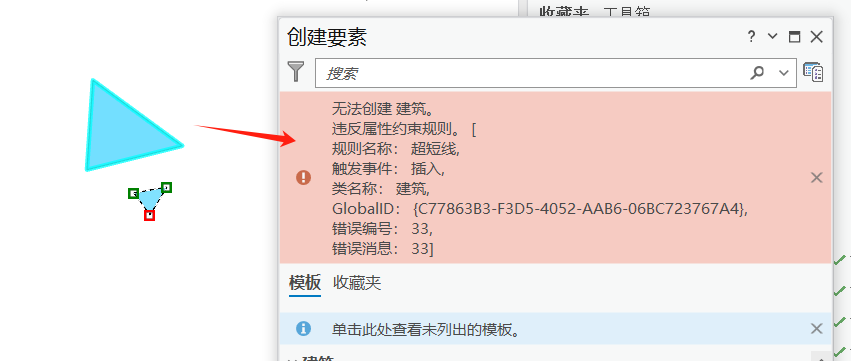
5、禁止尖锐角
通过计算相邻3个点之间的角度,可以禁止画出尖锐角。
将触发器选择为【插入、更新】,在表达式中输入:
// 获取环
var rings = geometry($feature)["rings"]
// 逐环处理
for(var i in rings){// 环内每个点处理for(var j=0; j < count(rings[i])-2; j++) {// 算角度 var ang = Angle(rings[i][j],rings[i][j+1],rings[i][j+2])// 保证在180度内if(ang>180)ang = 360-ang// 小于20度就报错if(ang<20)return false}
}
return true这里我省略了计算最后一个点的情况,要计算的话,需要把第一个点加到列表末尾,有兴趣的可以自己试试。
创建或修改的时候,如果边界点的角度小于20度,就会弹出错误:
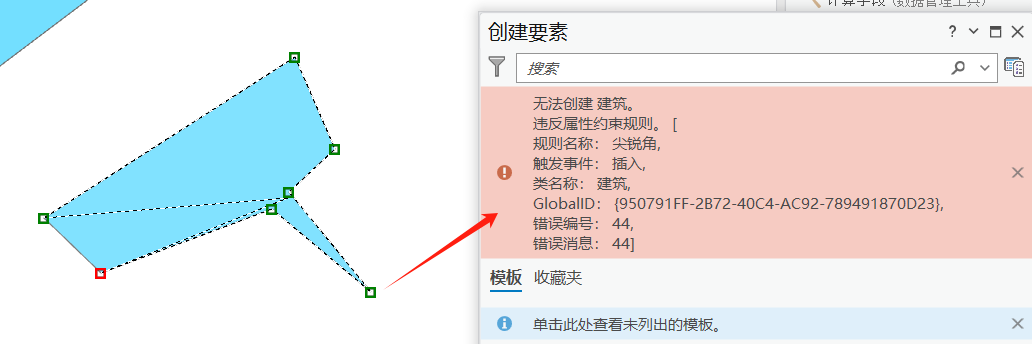
二、验证规则
验证规则用于验证数据集中的错误。根据规则对现有要素进行评估,如果违反规则,则会创建错误要素。
表达式写法和计算、约束差不多。
这部分软件预制了许多规则,点击即用型规则,可以看到如下:
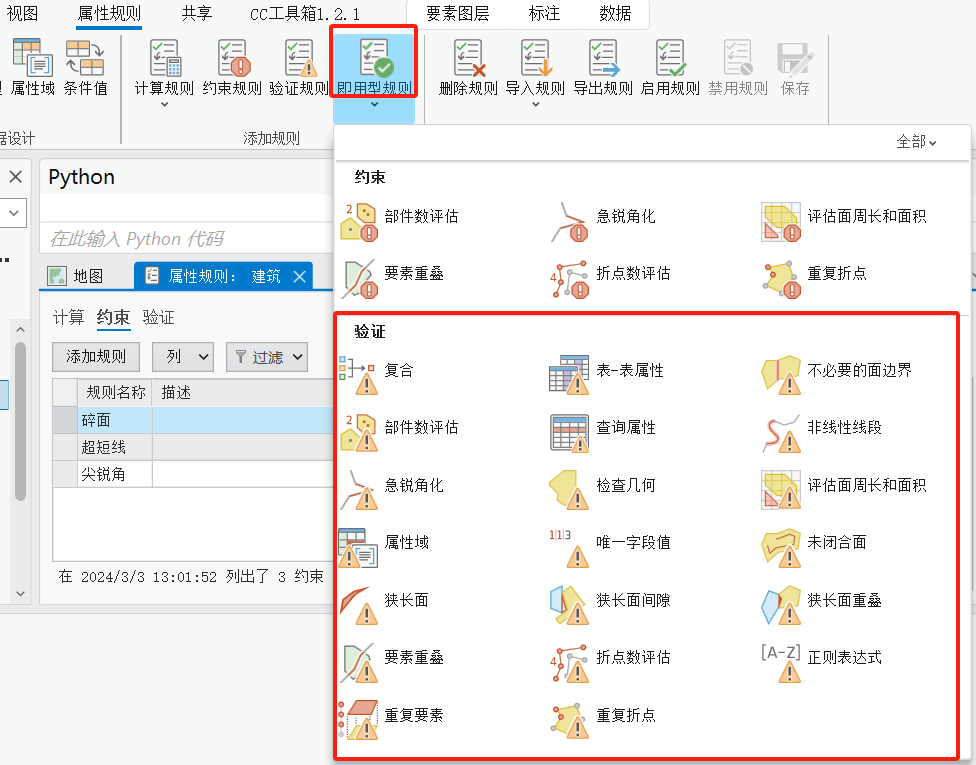
但是我试用过后,发现过程繁琐,而且有疑似bug,总之不太好用,有兴趣的可以自行尝试。
后面有空可以专门出一篇关于属性规则使用步骤的文章。