什么时候能用双指针？

（1）对撞指针：

①两数和问题中可以使用双指针，先将两数和升序排序，可以发现规律，如果当前两数和大于target，则右指针向左走。

②接雨水问题中，左边最大 和 右边最大 可以通过双指针 + 双变量维护。

（2）快慢指针：

①比如找到链表的中点，快指针一次走两步，满指针一次走一步。

（3）滑动窗口：

滑动窗口维护当前窗口内满足要求。而双指针可以在整个数组中考虑问题。

动态变化窗口大小：

①比如接雨水这里，考虑极限：满足右边界大于等于左边界，此时左边界移动。

固定窗口大小：

①找到字符串中所有字母异位词：固定窗口大小为目标串，移动记录窗口时，增加窗口末尾字符对应的个数，减少滑出窗口的字符对应的个数。

一、从单个水柱本身考虑

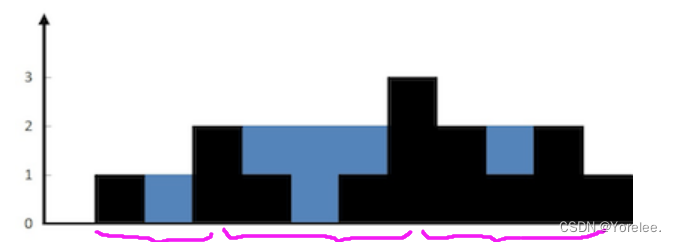
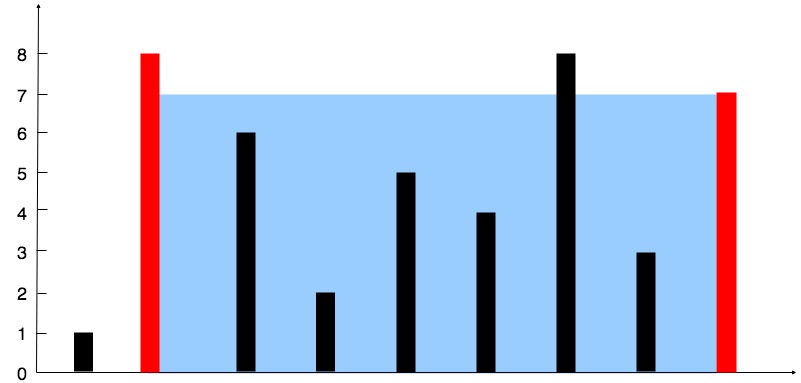
下标为i的水柱能接的雨水，取决于它左边最高的水柱 和 右边最高的水柱的最小值（包括它本身）。

        为了理解这一性质，我们可以这样想象：取出左边最高和最边最高的水柱，将其比作一个碗的边界。中间坑坑洼洼，忽高忽低，高低错落，碗面中的一个点的能接水的最高高度是多少呢？ 就是碗边界的最小值-该点的高度。

因此，从单个水柱考虑，我们只需要能够求出这个问题即可。

一、动态规划

我们定义两个数组：

left_max[i]：表示从0~i 中 水柱高度的最大值

right_max[i]： 表示从i~height.size()-1中水柱高度的最大值

class Solution {
public:int trap(vector<int>& height) {int n=height.size();vector<int> left_max(n);vector<int> right_max(n);left_max[0]=height[0];right_max[n-1]=height[n-1];//求出左边最大值for(int i=1;i<n;++i){left_max[i]=max(left_max[i-1],height[i]);}//求出右边最大值for(int i=n-2;i>=0;--i){right_max[i]=max(right_max[i+1],height[i]);}long long ans=0;for(int i=0;i<n;++i){ans+=min(left_max[i],right_max[i])-height[i];}return ans;}
};

二、双指针

class Solution {
public:int trap(vector<int>& height) {int n=height.size();int left_max=height[0];int right_max=height[n-1];int left=0;int right=n-1;long long ans=0;while(left<right){left_max=max(left_max,height[left]);right_max=max(right_max,height[right]);if(left_max>right_max){//说明右边这个right柱子 取决于 其右边的最高高度。ans+=right_max-height[right];--right;}else{ans+=left_max-height[left];++left;}}return ans;}
};

二、从整体水柱考虑

从左向右依次看，对于第一个水柱而言，直到遇到一个比它高的水柱，其中间的水柱都由第一个水柱的高度决定。一种特殊情况是，最后一个找不到比它高的水柱，此时对它我们从右往左看即可。（左右对称）

class Solution {
public:int trap(vector<int>& height) {int left=0;//左边指向当前左柱子，当左柱子低于右柱子时，它已经不再能装水了 int right=1;//右边往右一直寻找比左柱子高的 或 相等高度的柱子int sum=0;while(right<height.size()){if(height[right]>=height[left]){int temp=height[left];while(left!=right){sum+=temp-height[left];++left;}}++right;}if(left!=height.size()-1){int end=left;left=height.size()-1;right=left-1;while(right>=end){if(height[right]>=height[left]){int temp=height[left];while(left!=right){sum+=temp-height[left];--left;}}--right;}}return sum;}
};