https://link.springer.com/chapter/10.1007/978-3-030-65411-5_21

A compact, private, Multi-Party Confidential Transactions (MCT)

• 紧凑型多方机密交易（Compact MCT）：MCT的长度与常规的单一所有者交易一样短；换句话说，多方承诺、签名和范围证明与单方的承诺、签名和范围证明无法区分。
• 私密型多方机密交易（Private MCT）- 涉及多个方参与（以及他们的数量）的事实被隐藏起来。
• 提出两种结构:一个更简单的N方一致转移和一个通用的T/N阈值转移。

Intro

案例：

• 正常情况：
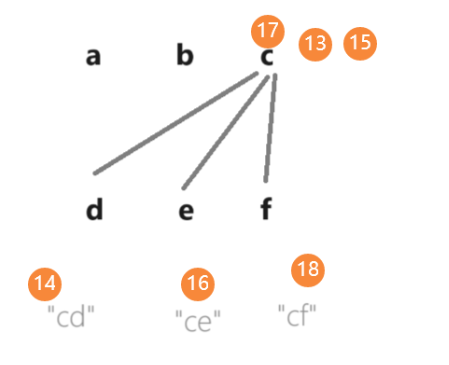
  Alice发送预交易$(C_{v,k_1+k_2},v,k_1)$给Bob、$(C_{v,k_1+k_2},v,k_2)$给Charles，意图是需要两个共同所有者的同意才能花费这些硬币，因为他们都不知道$k_1+k_2$。Bob和Charles随机生成各自的密钥$k_1^{\prime }$和$k_2^{\prime }$，并共享部分承诺，如$C_{Bob}=C_{v/2,k_1}$和$C_{Charles}=C_{v/2,k_2}$，旨在创建一个新的硬币束$C^{\prime }$：
  

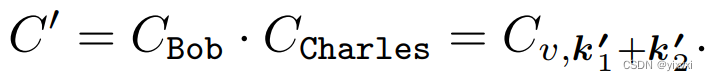
• 欺骗攻击：
  Bob等待Charles的部分交易承诺$C_{v/2,k_2}$，并与Charles共享一个欺骗性的部分承诺$C_{Bob}=C_{v/2,k_1}\cdot (C_{v/2,k_2}{)}^{-1}$。$C^{\prime }$变成：
  
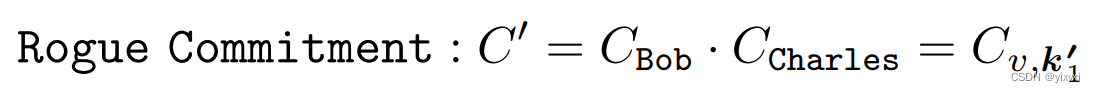
  现在，硬币可以不经过Charles同意被花费。

• 抵御恶意密钥攻击：Bob和Charles相互分享$P_{Bob}=C_{0,k_1^{\prime }}$和$P_{Charles}=C_{0,k_2^{\prime }}$。然后，他们各自计算：
  
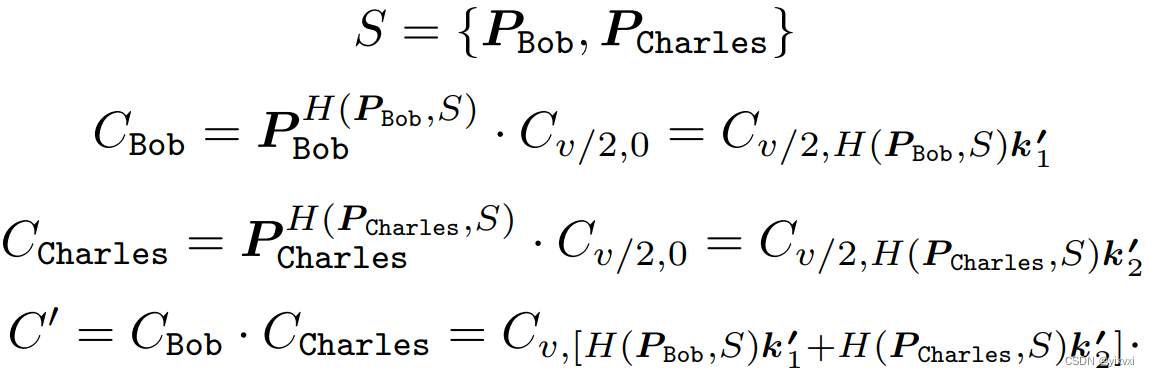
  （抗攻击的原理是哈希函数的单向性，计算$C_{Bob}$和$C_{Charles}$时对应的P已经固定）

• 但Bob仍然可以在交易上运行$C^{\prime }\cdot (P_{Charles}^{H(P_{Charles},S)}{)}^{-1}$
  ($=C_{Bob}\cdot C_{v/2,0}=C_{v,H(P_{Bob},S)k_1^{\prime }}$)
  解决：保密交易对$E=C^{\prime }\cdot C^{-1}$进行签名，而不是一个空消息，将$C^{\prime }$提交承诺给交易。

Preliminaries

Compact Multi Signature Scheme

定义：（其他安全性质见原文）

Non-interactive Zero-Knowledge Compact Multi-party Range Proofs

定义以下范围证明的完整性、稳健性、零知识、不可延展性以及对诚实但好奇的组合者的安全性。
（安全性定义略，见原文）

Compact Multi-party Confidential Transactions

（构建块的定义交代清楚了，正式给出机密交易的协议）
两种MCT协议和安全模型。注意，与签署空消息的麦克斯韦CT不同，MCT协议签署了多余的值E。

MCT所需的基本协议

Rogue Key Attack Resistant Commitment Generation.

通用多方资金转移

我们紧凑的私有MCT协议的工作原理如下。

• 资产或币束的共同所有人自己计算密钥，但与其他共同所有人共享公共信息。
• 最后，每个共同所有者生成部分交易，共同所有者(组合者)将部分交易组合起来生成最终交易。

$(\mathbf{v},\mathbf{k},\mathbf{C})$是输入的硬币束，$\mathbf{\rho }$是输出的硬币数量数组（每组都是共享账户，有多个接收者），应该发送到$|\mathbf{m}|(=|\mathbf{\rho }|)$组接收者，其中每组$i$由$m_i$个接收者组成。

资金发送功能MCT.Send

资金发送功能MCT.Send通过发送交易$tx$来根据$\mathbf{\rho }$隔离硬币，并将密钥分配为$\mathbf{ptx}$用于N-fund转账或$\mathbf{tptx}$用于T/N-fund转账，其中$m_i$个接收方中的$t_i$个必须同意花费硬币束$i$。为了功能实现，我们一起输入盲密钥集$\mathbf{k}$。但是，${\mathbf{k}}_{j,i^{\prime }}$是属于第$i^{\prime }$(输入币束)的第$j$个共同所有者的部分秘密密钥，并且部分密钥不与任何人共享。

$\mathbf{m}$-接收方共享账户数组，每个$m_i$代表一个接收者账户的共享所有者数量。
（交易的输出一般等于发送给接收方的若干账户+找零账户，所以$|\mathbf{\rho }|=|\mathbf{m}|=|{\mathbf{v}}^{\prime }|-1$）
$\mathbf{v},{\mathbf{v}}^{\prime }$-交易输入、输出金额数组，${\sum }_{j=1}^n\mathbf{v}={\sum }_{i=1}^{|\mathbf{\rho }|+1}{\mathbf{v}}^{\prime }$
$\mathbf{\rho }$-除找零外的交易输出

• 首先是合法性验证和密钥生成，有n个co-owner，每个co-o j有一组主密钥${\mathbf{k}}_j,{\mathbf{P}}_j$，面向每个账户各有一个分量，因为输入账户有$|v|$个，所以每个主密钥都有对应的共$|v|$个分量。
• 输入小于输出，确保输入账户有足够的金额进行合法花费
• 分享${\mathbf{P}}_j$后，每个co-owner分别计算本次交易输出的交易密钥对
• 当有余额时，将余额作为一个新的输出，为余额新初始化一组交易密钥。
  
  每个co-owner，分别计算：
• 把余额的交易密钥分量加入输出账户的主密钥集中
• 生成自己的部分交易，并分享
• 用收到的所有部分交易，计算总共的E
• 验证E的合法性：$({\prod }_{i^{\prime }=1}^{|{\mathbf{v}}^{\prime }|}{g}^{{\mathbf{sk}}_{i^{\prime }}}\cdot h^{\sum \mathbf{v}})\cdot \prod {\mathbf{C}}^{-1}$，如果$\sum v=\sum v^{\prime }$，E合法
• 生成总签名和证明
• 整合方将所有部分交易补全为总交易。

（这段是交易的发送方的操作，所有的co-owner拿出共同拥有的$|v|$个输入账户，$v^{\prime }$个输出账户，需要的话，输出账户中包含一个新生成的找零账户，签名固定所有交易信息和交易密钥；交易合法性验证；输出账户的范围证明）

两种情况：

• 门限为空，直接返回交易；（每个输出账户的使用都不设门限，所有co-owner同意才能交易）
• 有输出账户的门限大于0，秘密共享SS生成交易。
  

Threshold Key Sharing

我们使用Shamir秘密共享(SS)方案[23]，其中有t个交易商，t为阈值。每个交易商分别选择一个秘密主密钥，最终密钥是所有t个主密钥的总和。

资金接收方MCT.Receive

• 共同接收方初始化接收账户的交易密钥，生成部分交易，并共享
• 用接收到的所有部分交易整合成总体的E值
• 验证E值
• 共同所有者生成的总体签名和范围证明，整合