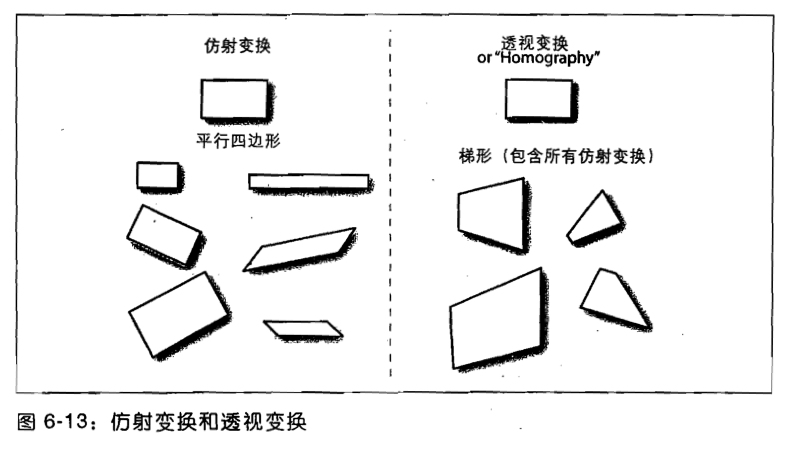
仿射变换矩阵通常是2x3的矩阵。
三个特点：

1. 直线依然是直线
2. 平行线依然平行
   $$\begin{array}{c}\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}a11& a12& b1\\ a21& a22& b2\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]\\ x^{\prime }=a11\ast x+a12\ast y+b1\\ y^{\prime }=a21\ast x+a22\ast y+b2\end{array}$$

上面的式子表示2D点乘以一个矩阵后加上平移(b1,b2)。

透视变换是3x3的矩阵。
$$\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=\left[\begin{array}{ccc}a11& a12& b1\\ a21& a22& b2\\ c1& c2& c3\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

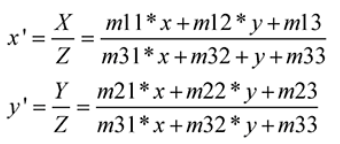
z’ = 1

总的来说，仿射变换保持了更多的几何性质，适用于描述相对简单的几何变换，如平移、旋转、缩放和错切。而透视变换则更加灵活，能够描述更复杂的几何变换，如近大远小的透视效果。