a.28. 找出字符串中第一个匹配项的下标

题目链接

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回  -1 。

示例 1：

输入：haystack = "sadbutsad", needle = "sad"
输出：0
解释："sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ，所以返回 0 。

示例 2：

输入：haystack = "leetcode", needle = "leeto"
输出：-1
解释："leeto" 没有在 "leetcode" 中出现，所以返回 -1 。

思路：利用kmp算法减少回退步数

        

        KMP主要应用在字符串匹配上。

        KMP的主要思想是当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。所以如何记录已经匹配的文本内容，是KMP的重点，也是next数组肩负的重任。

        next数组就是一个前缀表（prefix table），前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

        

        文章中字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。

后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。

        正确理解什么是前缀什么是后缀很重要!因为前缀表要求的就是相同前后缀的长度。

接下来就要说一说怎么计算前缀表。

如图：

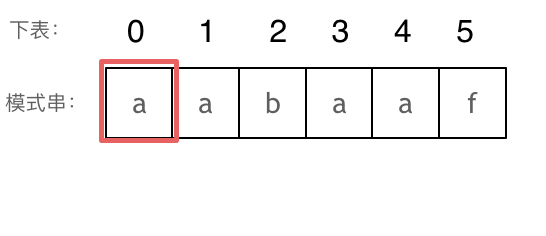
长度为前1个字符的子串a，最长相同前后缀的长度为0。（注意字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。）

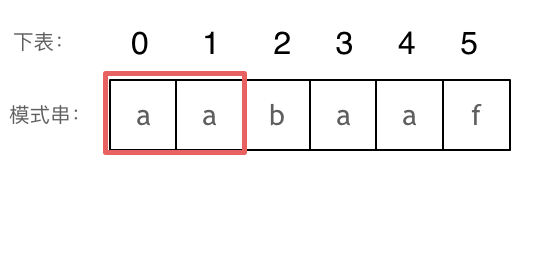
长度为前2个字符的子串aa，最长相同前后缀的长度为1(a)。

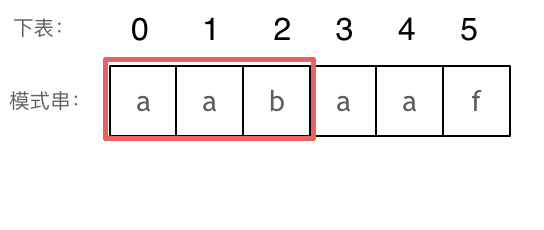
长度为前3个字符的子串aab，最长相同前后缀的长度为0。

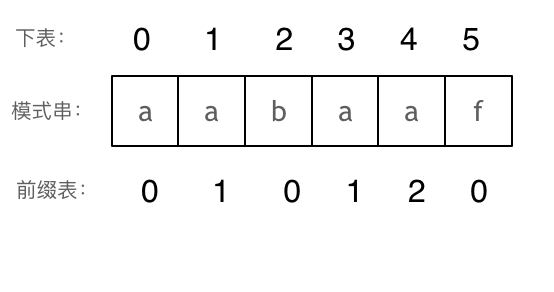
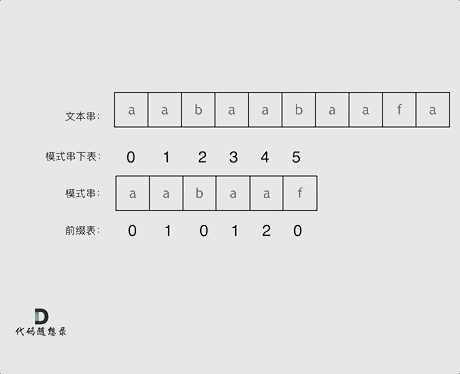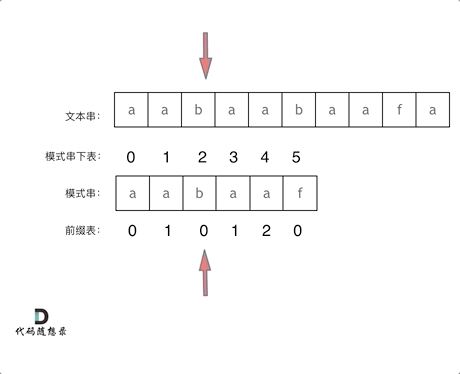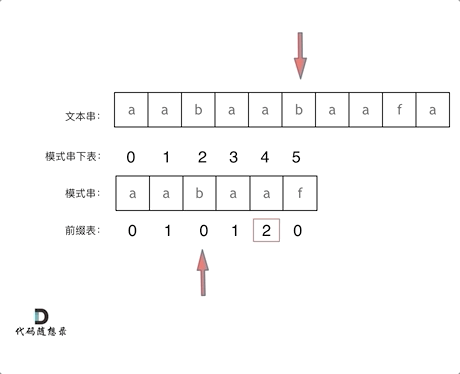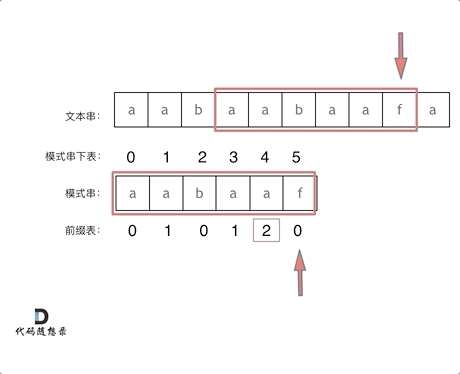
以此类推： 长度为前4个字符的子串aaba，最长相同前后缀的长度为1（a)。 长度为前5个字符的子串aabaa，最长相同前后缀的长度为2(aa)。 长度为前6个字符的子串aabaaf，最长相同前后缀的长度为0。

那么把求得的最长相同前后缀的长度就是对应前缀表的元素，如图： 

可以看出模式串与前缀表对应位置的数字表示的就是：下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示：

找到的不匹配的位置， 那么此时我们要看它的前一个字符的前缀表的数值是多少。

为什么要前一个字符的前缀表的数值呢，因为要找前面字符串的最长相同的前缀和后缀。

所以要看前一位的 前缀表的数值。

前一个字符的前缀表的数值是2， 所以把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。

最后就在文本串中找到了和模式串匹配的子串了。

#前缀表与next数组

很多KMP算法的实现都是使用next数组来做回退操作，那么next数组与前缀表有什么关系呢？

next数组就可以是前缀表，但是很多实现都是把前缀表统一减一（右移一位，初始位置为-1）之后作为next数组。

class Solution {
public:void getnextarry(int* next,const string& s){//前缀表-1的写法int j=-1;next[0]=j;for(int i=1;i<s.size();i++){while(j>=0&&s[i]!=s[j+1]){j=next[j];//不相等，回退}if(s[i]==s[j+1]){j++;//相等，继续移动}next[i]=j;//记录前后缀}}int strStr(string haystack, string needle) {if(needle.size()>haystack.size())return -1;if(needle.size()==0)return 0;int next[needle.size()];getnextarry(next,needle);//生成前缀表int j=-1;for(int i =0;i<haystack.size();i++){while(j>=0&&haystack[i]!=needle[j+1]){j=next[j];}if(haystack[i]==needle[j+1]){j++;}//j==needle.size()-1说明模式串遍历完成，找到了对应//则此时文本串中匹配的部分起点=i-模式串长度if(j==needle.size()-1)return (i-needle.size()+1);}return -1;}
};

//前缀表不-1的写法
class Solution {
public:void getNext(int* next, const string& s) {int j = 0;next[0] = 0;for(int i = 1; i < s.size(); i++) {while (j > 0 && s[i] != s[j]) {j = next[j - 1];//用前一步的next数组元素回退}if (s[i] == s[j]) {j++;}next[i] = j;}}int strStr(string haystack, string needle) {if (needle.size() == 0) {return 0;}int next[needle.size()];getNext(next, needle);int j = 0;for (int i = 0; i < haystack.size(); i++) {while(j > 0 && haystack[i] != needle[j]) {j = next[j - 1];}if (haystack[i] == needle[j]) {j++;}if (j == needle.size() ) {return (i - needle.size() + 1);}}return -1;}
};

b.459.重复的子字符串

题目链接

给定一个非空的字符串 s ，检查是否可以通过由它的一个子串重复多次构成。

示例 1:

输入: s = "abab"
输出: true
解释: 可由子串 "ab" 重复两次构成。

示例 2:

输入: s = "aba"
输出: false

示例 3:

输入: s = "abcabcabcabc"
输出: true
解释: 可由子串 "abc" 重复四次构成。 (或子串 "abcabc" 重复两次构成。)

提示：

• 1 <= s.length <= 104
• s 由小写英文字母组成

思路：

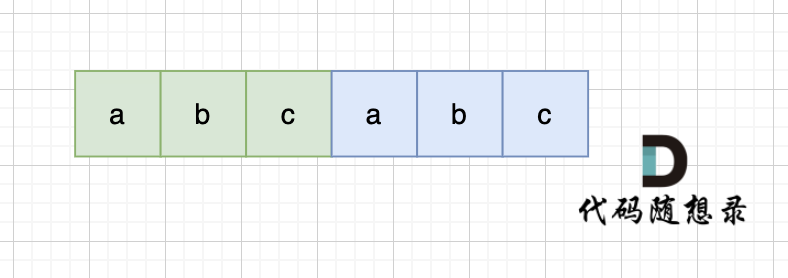
一个字符串s：abcabc，内部由重复的子串组成，那么这个字符串的结构一定是这样的：

也就是由前后相同的子串组成。

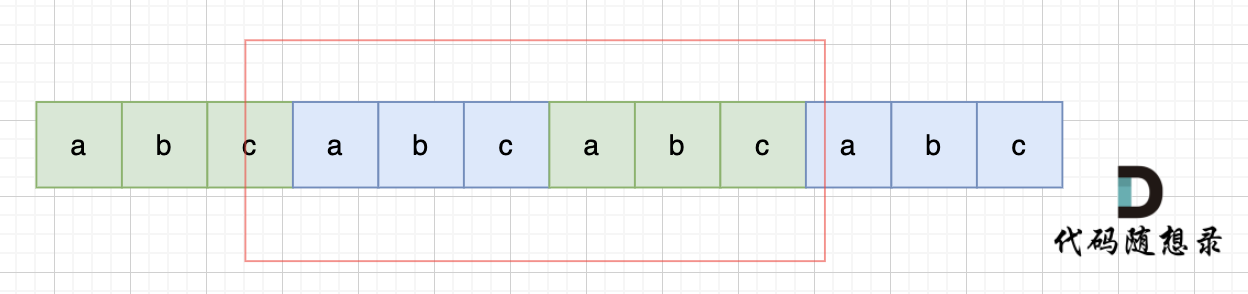
那么既然前面有相同的子串，后面有相同的子串，用 s + s，这样组成的字符串中，后面的子串做前串，前面的子串做后串，就一定还能组成一个s，如图：

所以判断字符串s是否由重复子串组成，只要两个s拼接在一起，里面还出现一个s的话，就说明是由重复子串组成。

当然，我们在判断 s + s 拼接的字符串里是否出现一个s的的时候，要刨除 s + s 的首字符和尾字符，这样避免在s+s中搜索出原来的s，我们要搜索的是中间拼接出来的s。

class Solution {
public:bool repeatedSubstringPattern(string s) {string t=s+s;t.erase(t.begin()); t.erase(t.end()-1);if(t.find(s)!=std::string::npos)return true;return false;}
};