3047. 求交集区域内的最大正方形面积

难度：中等

问题描述：

在二维平面上存在 n 个矩形。给你两个下标从 0 开始的二维整数数组 bottomLeft 和 topRight，两个数组的大小都是 n x 2 ，其中bottomLeft[i]和topRight[i]分别代表第i个矩形的左下角和右上角坐标。我们定义向右的方向为x轴正半轴x坐标增加），向左的方向为x轴负半轴（x坐标减少）。

同样地，定义 向上的方向为y轴正半轴（y 坐标增加），向下 的方向为 y 轴负半轴（y 坐标减少）。你可以选择一个区域，该区域由两个矩形的交集形成。你需要找出能够放入该区域内的最大正方形面积，并选择最优解。

返回能够放入交集区域的正方形的最大可能面积，如果矩形之间不存在任何交集区域，则返回 0。

示例 1：

输入：bottomLeft = [[1,1],[2,2],[3,1]], topRight = [[3,3],[4,4],[6,6]]

输出：1

解释：边长为 1 的正方形可以放入矩形 0 和矩形 1 的交集区域，或矩形 1 和矩形 2 的交集区域。因此最大面积是边长 * 边长，即 1 * 1 = 1。

可以证明，边长更大的正方形无法放入任何交集区域。

示例 2：

输入：bottomLeft = [[1,1],[2,2],[1,2]], topRight = [[3,3],[4,4],[3,4]]

输出：1

解释：边长为 1 的正方形可以放入矩形 0 和矩形 1，矩形 1 和矩形 2，或所有三个矩形的交集区域。因此最大面积是边长 * 边长，即 1 * 1 = 1。

可以证明，边长更大的正方形无法放入任何交集区域。

请注意，区域可以由多于两个矩形的交集构成。

示例 3：

输入：bottomLeft = [[1,1],[3,3],[3,1]], topRight = [[2,2],[4,4],[4,2]]

输出：0

解释：不存在相交的矩形，因此，返回 0 。

分析：
拿到题目之后，大致上的思路：
1、先将两个矩形交集上能产生的最大正方形面积求出
由此设计函数max_square(one,two)，其中one和two表示两个矩形，其数据格式为[bottomLeft,topRight]，bottomLeft和topRight分别是矩形左下角和右上角坐标
2、对于多个矩形，先将矩形两两组合交集上产生的最大正方形面积分别求出，然后找出其中的最大值即为问题的解

思路虽说理出来了，但问题的关键是如何设计出计算两个矩形交集上产生最大正方形面积的函数max_square(one,two)？
我在草稿纸上画了几种两个矩形相交或不相交的图，分析来分析去，总感觉涉及的要素多，难以理出头绪，很是考查一个人耐心和细致方面的素质
经过反复思考，最后确定水平方向两个矩形是否相交与竖直方向两个矩形是否相交没有相关性，因此可以考虑单独分析水平方向和竖直方向。只要分析清楚水平方向的情况，竖直方向应该可以类似处理
先看水平方向，因为不考虑竖直方向，所以可以用两条水平线段代替两个矩形，如图1所示。
分别用

xoL表示矩形one的左下角横坐标
xoR表示矩形one的右上角横坐标
xtL表示矩形two的左下角横坐标
xtR表示矩形two的右上角横坐标
 

从图1可以看出矩形one和two在水平方向上的交集为w=min(xoR,xtR)-max(xoL,xtL)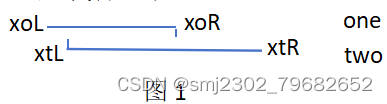
从图2可以看出w=min(xoR,xtR)-max(xoL,xtL)=xoR-xtL<0，两个矩形 没有交集

从图3可以看出w=min(xoR,xtR)-max(xoL,xtL)=xtR-xoL<0，两个矩形没有交集

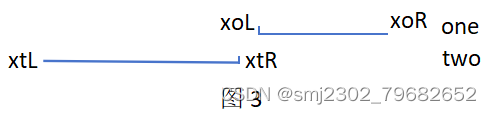
从图2图3可以推测出，如果w=0，只表示有左右边界的重合，交集依然为0
从上面的情况可以看出，只要w=min(xoR,xtR)-max(xoL,xtL)>0，在水平方向上就一定有交集，且交集长度为w

根据同样的道理，在竖直方向上，同样不考虑水平方向，可以用两条竖直线段代替两个矩形
分别用

yoL表示矩形one的左下角纵坐标
yoR表示矩形one的右上角纵坐标
ytL表示矩形two的左下角纵坐标
ytR表示矩形two的右上角纵坐标
则只要h=min(yoR,ytR)-max(yoL,ytL)>0,在竖直方向上也一定有交集，且交集长度为h

因此交集区域上的最大正方形边长应该为a=min(w,h)，最大正方形面积也就可以求出了

程序如下：

def max_square(one,two):#one,two表示两个矩形区域其数据格式为[[左下角坐标x,y],[右上角坐标x,y]]    xoL=one[0][0] yoL=one[0][1]xoR=one[1][0]yoR=one[1][1]    xtL=two[0][0]ytL=two[0][1]xtR=two[1][0]ytR=two[1][1]w=min(xoR,xtR)-max(xoL,xtL)h=min(yoR,ytR)-max(yoL,ytL)if w>0 and h>0:return min(w,h)*min(w,h)else:return 0bottomLeft=eval(input('bottomLeft='))
topRight=eval(input('topRight='))
recTanges=list(zip(bottomLeft,topRight))
n=len(recTanges)
s=[]
for i in range(n-1):    for j in range(i+1,n):s.append(max_square(recTanges[i],recTanges[j]))
print(max(s))

运行实例1
bottomLeft=[[1,1],[2,1]]
topRight=[[4,3],[5,4]]
4

运行实例2
bottomLeft=[[1,1],[2,2],[3,1]]
topRight=[[3,3],[4,4],[6,6]]
1

运行实例3
bottomLeft=[[1,1],[3,3],[3,1]]
topRight=[[2,2],[4,4],[4,2]]
0

感悟：要善于从纷繁复杂的数据关系中理出关键要素，从而简化问题求解。