在进入Bootstrap 图之前,让我们先了解一下Bootstrap(或Bootstrap 抽样)是什么。
Bootstrap 抽样(Bootstrap Sampling):这是一种方法,我们从一个数据集中重复地取一个样本数据来估计一个总体参数。它用于确定总体的各种参数。
Bootstrap图
Bootstrap图是从数据样本计算的统计量分布的图形表示。它通常用于可视化统计量的可变性和不确定性,例如平均值或标准差,通过显示统计量在许多Bootstrap数据样本上的分布。
在bootstrap图中,x轴表示统计量的值,y轴表示这些值的频率。为每个Bootstrap样本绘制一条线,线的高度表示该样本中统计值的频率。线的分布表示统计量在Bootstrap样本上的分布。
Bootstrap图是理解统计量中的不确定性的强大工具,特别是当数据的潜在分布未知或复杂时。它还可以用来生成统计量的置信区间,并比较不同统计量的分布。
需要注意的是,Bootstrap是一种重新估计技术,用于估计样本中统计量的不确定性,而无需对数据的潜在分布进行任何假设。它可用于估计标准误差、置信区间和执行假设检验。
Bootstrap plot:Bootstrap plot是一种图形方法,用于测量总体的任何期望统计特征的不确定性。它是置信区间的一种替代方法。(也用于计算统计量的数学方法)。
如何使用Bootstrap
通常,我们可以用数学方法计算总体统计量的不确定性,使用置信区间。然而,在许多情况下,推导出的不确定性公式在数学上是难以处理的。在这种情况下,我们使用Bootstrap plot。
假设,我们有5000人在一个公园里,我们需要找到整个人口的平均体重。测量每个人的体重然后取平均值是不可行的。这就是bootstrap抽样的用武之地。
我们从人群中随机抽取5人一组,然后求出平均值。然后,我们做同样的过程8-10次。通过这种方式,我们可以更有效地获得对总体平均权重的良好估计。
举个例子:
让我们考虑一个例子,了解Bootstrap图如何使从大量人口中获得关键信息变得更容易。假设我们有3000个随机生成的统一数字的样本数据。我们取出30个数字的子样本,并找到其平均值。我们对另一个随机子样本再次这样做,依此类推。
我们绘制了上述信息的bootstrap 图,只需查看它,我们就可以很容易地给予关于所有3000个数字的平均值的很好的估计。还有各种其他有用的信息可以从bootstrap 图中获得,例如:
- 哪个子样本的方差最小,
- 哪个子样本创建最小置信区间等。
Python简单实现
import pandas as pd
import numpy as nps = pd.Series(np.random.uniform(size=500))
pd.plotting.bootstrap_plot(s)
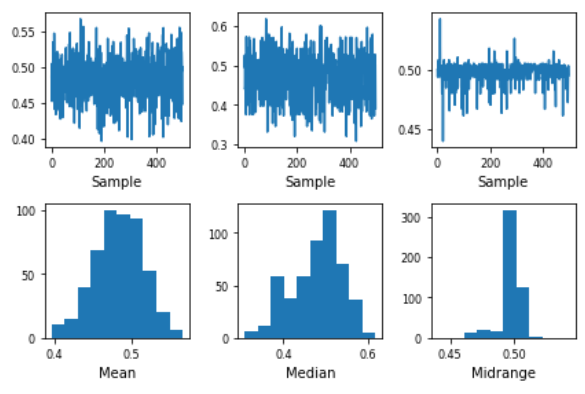
说明:
- Bootstrap图给出了总体所需信息的估计值,而不是精确值。
- 它高度依赖于给定的数据集。当大量子集具有重复样本时,它不能给予好的结果。
- 当我们获得的信息高度依赖于尾值时,Bootstrap图变得无效。
Bootstrap的优缺点
优点:
- 它是一种非参数方法,这意味着它不需要对数据的潜在分布进行任何假设。
- 它可用于估计各种统计量的标准误差和置信区间。
- 它可以用来估计统计量的不确定性,即使样本量很小。
- 它可用于执行假设检验和比较不同统计量的分布。
- 在统计、金融、机器学习等多个领域有着广泛的应用。
缺点:
- 它可能是计算密集型的,特别是在处理大型数据集时。
- 它可能不适用于所有类型的数据,例如高度偏斜或重尾分布。
- 它可能不适合估计具有非常大方差的统计数据的不确定性。
- 它可能不适用于估计不平滑或方差差异很大的统计数据的不确定性。
- 它可能并不总是一个很好的替代其他统计方法,如渐近方法,当大样本量可用时。