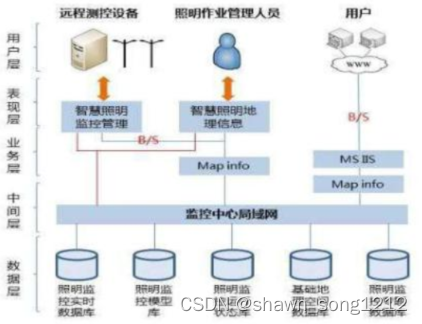
一、说明
T傅里叶级数及其伴随的推导是数学在现实世界中最迷人的应用之一。我一直主张通过理解数学来理解我们周围的世界。从使用线性代数设计神经网络,从混沌理论理解太阳系,到弦理论理解宇宙的基本组成部分,数学无处不在。
当然,这些是数学中更复杂和技术性的应用。但是,将数学应用于我们的生活呢?
好吧,也许你在学习时会听双耳节拍。或者您以前做过 X 光检查。或者,您可能已经看过脑电图 (EEG) 测试的实际应用。
无论情况如何,总有一些数学算法可以促进它们的使用。
但是哪种算法呢?
Welp,其中之一是傅里叶级数(及其衍生物)。
二、一丝直觉
傅里叶级数及其推导的核心是数学算法,旨在将信号从时域转换为频域。
在一段时间内分析时域中的信号。
在频域的功率谱上分析频域中的信号
它通过接收信号函数并将其分解为具有不同频率和不同功率水平的正弦函数的总和来做到这一点。

傅里叶级数的一个非常基本的表示。
从傅里叶级数中,我们可以推导出连续傅里叶变换,它可以让我们隔离构成信号的各个频率分量及其相应的功率。
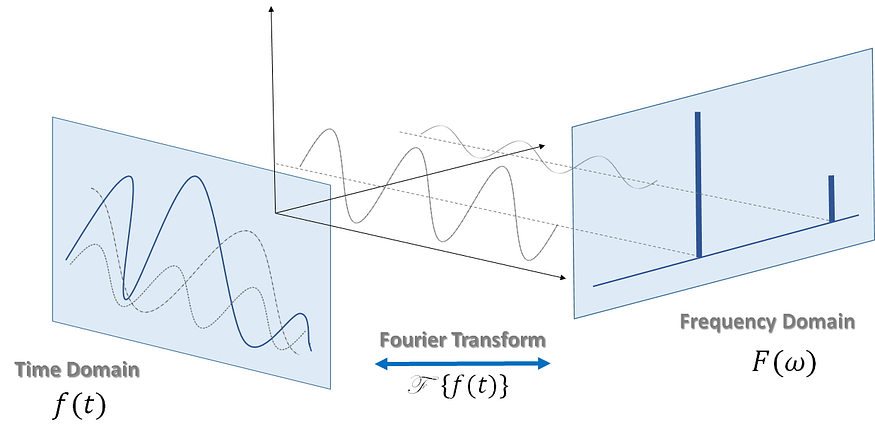
傅里叶变换的可视化。
这种变换非常有用,因为一旦我们将信号从时域转换为频域,我们就可以从信号中去除不需要的频率分量。
举个例子,假设我们使用脑电图来记录大脑信号以分析多动症。
通常,通过脑电图记录的信号非常嘈杂,不是很可靠——至少原始脑电图信号不是。
我们可以使用傅里叶级数的另一种推导,即快速傅里叶变换,以便将原始脑电信号从时域分解到频域。

时域(左)和频域(右)
从那里,我们可以通过实现带通、带阻或陷波滤波器从数据集中删除特定的频率或频率范围。
您可以清楚地看到 EEG 数据集的频域中的巨大尖峰(可能来自电力线干扰)。
这些是我们通过应用滤波器去除的频率。

过滤脑电图数据集 |感谢 FFT。
这正是我在之前的一个项目中所做的,以描述ADHD。
如果您好奇,请随时在本文或视频中查看。
在许多其他应用中也可以做到这一点,例如音频工程、图像处理、医疗诊断和语音识别。
它不受限制。
现在,您可能已经注意到,我提到了傅里叶级数的不同推导,其中一些是傅里叶变换和快速傅里叶变换。
傅里叶级数的不同推导适用于不同的上下文。有些比其他的更实用,有些则更适合数学理论。
例如,连续傅里叶变换在无限级数上获取连续的非周期信号。

连续傅里叶变换公式
但是计算机不能处理连续信号,而且很可能你需要处理更有限的信号样本。
因此,我们可以改用离散傅里叶变换,它在 N 个样本上接收有限信号。

离散傅里叶变换公式
像这样的推导使我们的生活变得更加轻松。
现在,您可以轻松地从前一个转换中从数学上推导出每个转换。

这一切都是相互关联的。
当我在脑电图和信号处理领域工作时,我对傅里叶系列必须针对不同用例进行模塑的敏捷性着迷。
因此,我决定研究并学习每个变换背后的数学原理。
让我们更深入地了解一下它是如何工作的。
三、真正的傅里叶级数
实傅里叶级数是其他派生变换的基础工具。
如前所述,它允许我们表示连续
周期性信号,即在一段时间内重复的信号,变成正弦和余弦的总和。

实数傅里叶级数的基本表示
将函数分解为正弦曲线可以让我们更精确地分析函数,因为我们现在能够理解构成函数的底层组件。
现在,假设您有由分量 z n 表示的向量 z。

该向量可以用正交基 bn 表示,使用公式,
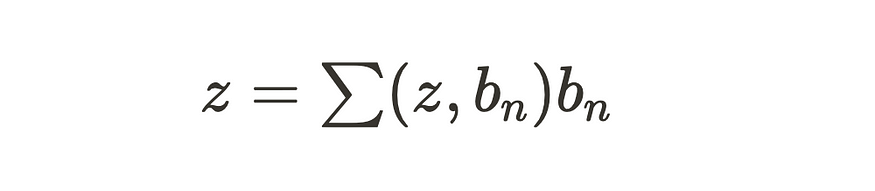
内部 (z, bn) 是 z 和基向量 bn 之间的点积。
因此,此公式可以应用于函数。
例如,假设我们有函数 f 和 g,它们的乘积是积分。这两个函数都是周期性的,周期为 T。

通过应用前面的公式,函数 f 和 g 可以重写为:

因此,实傅里叶级数允许我们使用基 bk = {fn}⋃{gn} 重写一组函数。
基函数 bn 是两组不同函数 fn 和 gn 的组合,可以写成:

其中 n ≥ 0。
因此,让我们将其应用于一个新函数。
现在假设我们有一个定义为 f 的信号。
我们可以将函数 f 重写为实傅里叶级数,并进行基数更改(如上所示)。

其中,内部系数 an 和 bn 由以下定义。
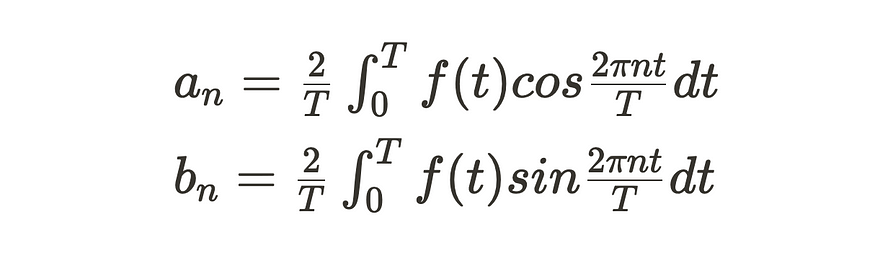
当应用于信号及其相应的频率时,n是表示频率分量的指数,t是时间,T是完整周期,系数an和bn是不同频率分量的幅度。
澄清一下,a₀ 不在实傅里叶级数的总和之和之外,因为它表示信号的直流 (DC) 分量。它是一个常数项,表示周期信号在一个周期内的平均值。
在实傅里叶级数中使用这个术语可以证明对于设置信号的“中心”或“基线”很有用。从那里,我们可以更有效地分析基线的交流电 (AC)。
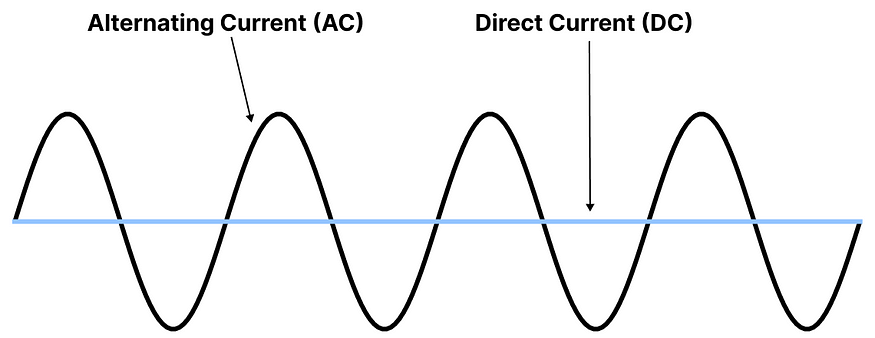
因此,最终,实傅里叶级数是系数 a 或 bn 与正弦曲线的乘积之和。
有趣吧?
好吧,这仅仅是个开始。
四、复傅里叶级数
复傅里叶级数实际上与真正的傅里叶级数相同,至少在它们的用途上是这样。它们都旨在将周期信号表示为正弦曲线的总和。
但关键的区别在于它们如何表示信号。
复傅里叶级数不是将正弦和余弦的单独求和相加,而是在奇异复指数下表示它们。

就像这样:)
系数 an 和 bn 也可以在奇异变量 cn 下捕获。
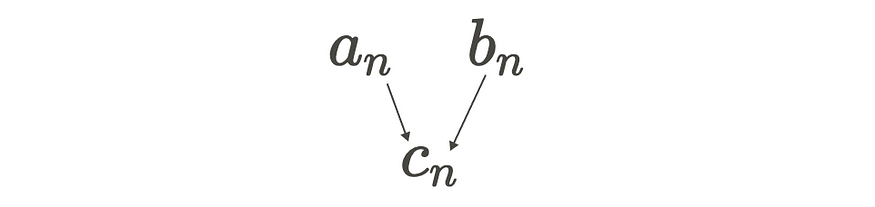
因此,复傅里叶级数是实傅里叶级数的更紧凑和简单的表示。
让我们从推导开始。
请记住,当应用于真实信号时:
n 是表示频率分量
的指数 t 是时间
T 是信号的整个周期
幸运的是,莱昂哈德·欧拉(Leonhard Euler,一位非常有趣的数学家)给了我们欧拉公式。
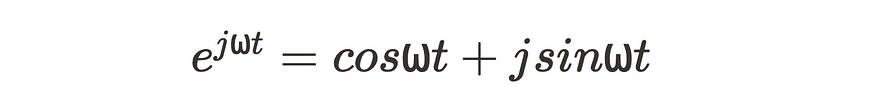
j 是虚单位。
⍵ 设置为角频率:

它基本上表示 2 个正弦曲线的总和与复指数之间的等价性。
通过欧拉公式,我们可以使用指数推导出正弦和余弦的三角恒等式。

如果你很好奇,你可以在这里查看完整的推导
因此,给定实傅里叶级数(根据 ⍵ 重写),
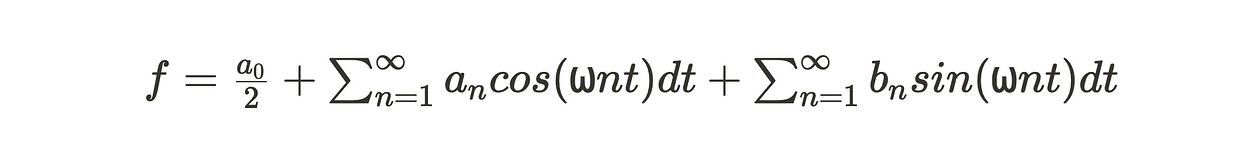
和欧拉公式,我们可以将其改写为
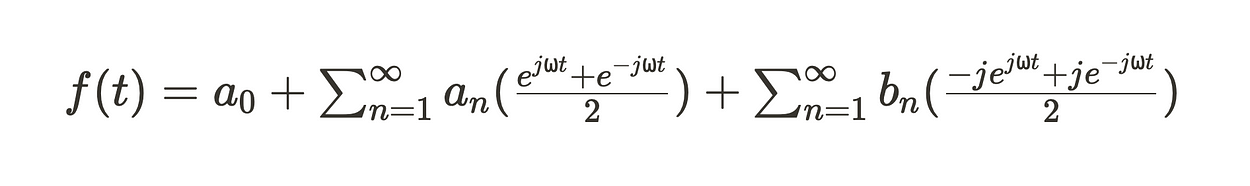
可以简化为

您可能会注意到第二个求和具有负指数。但我们希望它是一个正指数,以获得 ej⍵ⁿt 的两个求和。
因此,我们可以将 n 转换为负 n 并重写求和

现在我们有:

为了进一步简化这一点,我们可以用新的系数 cn 重写包含系数 an 和 bn 的内部表达式。

现在,系数 cn 基本上表示从 -∞ 到 ∞ 的所有可能的复系数。
因此,鉴于此,我们不需要用单独的求和来表示我们的方程。我们可以使用系数 cn 将它们连接在一个奇异求和中。
我们得到了复傅里叶级数。
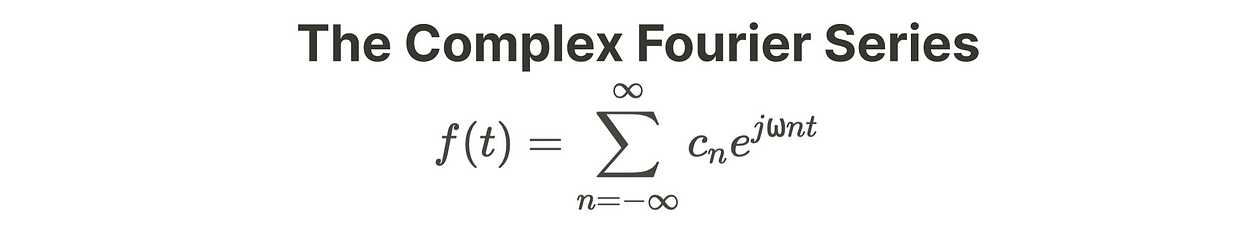
现在,系数 cn 的符号可以通过复傅里叶级数推导出来。
这种推导将允许我们找到系数 cn,而无需求解 an 和 bn。
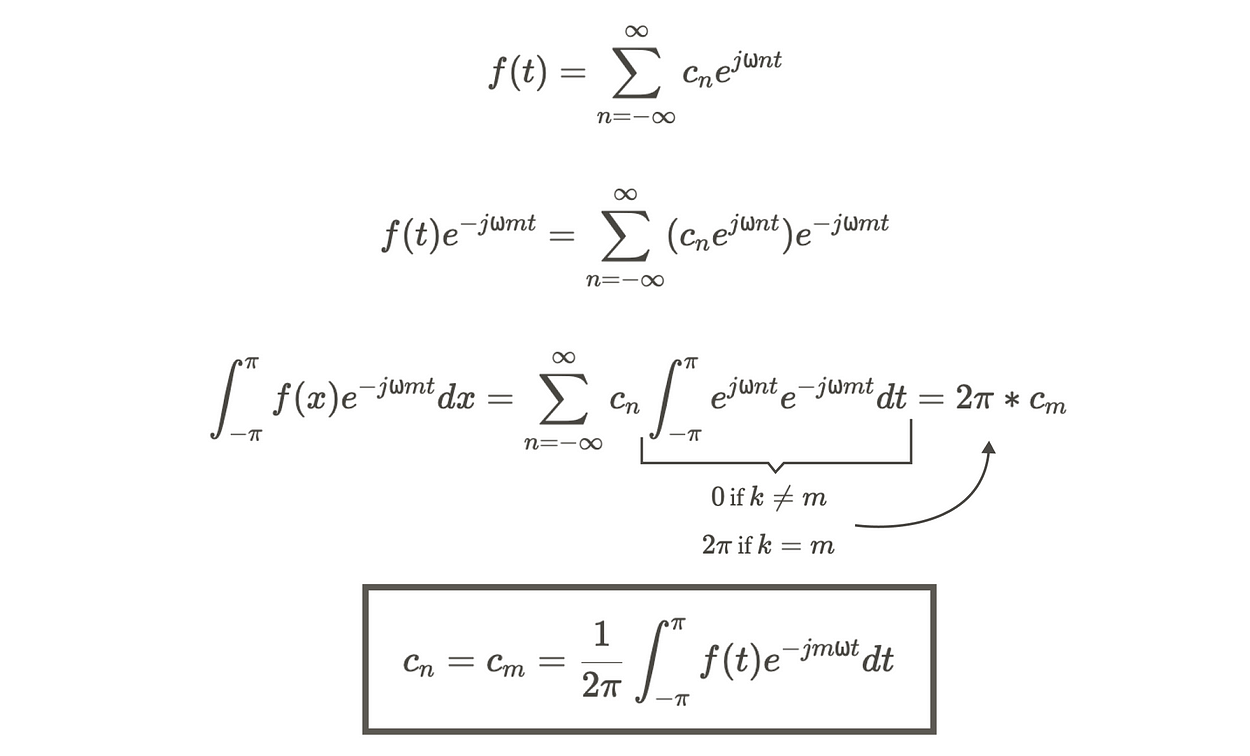
顺便说一句,我们使用 m 作为虚拟变量。它等价于 n,将其视为占位符。我们可以用 n 代替 m。
最终,作为复傅里叶级数,我们有:
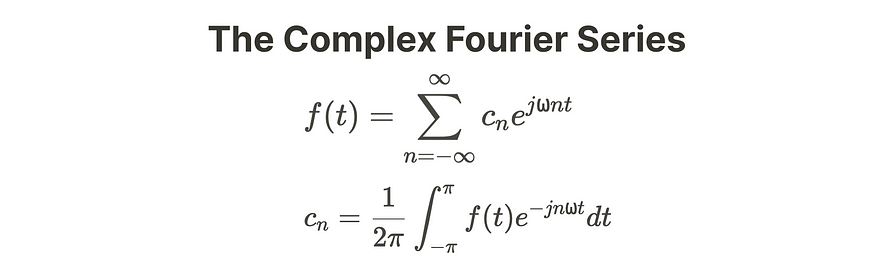
在周期 T 或 2π 上,从 -π 到 π。
快速提醒一下,除了实傅里叶级数之外,所有复傅里叶级数都是另一种将连续周期信号表示为 正弦曲线之和的方法。
区别在于使用复数指数,而且简单。
现在,进入连续傅里叶变换
五、连续傅里叶变换
到现在为止,你可能会问,“所有这些推导之间到底有什么区别?
嗯,区别在于它们如何应用以及它们可以应用于什么。
实数和复数傅里叶级数都适用于连续和周期信号。意思是长度无限大的均匀信号。

其他派生适用于不同类型的信号,例如离散信号或非周期信号。
在连续傅里叶变换的情况下,它是为连续和无限但非周期性的信号而设计的。

那么,让我们深入了解推导
让我们再看一下我们的复系数 cn。

从本质上讲,为了得到连续傅里叶变换,我们取 cn 及其无穷大的极限,将其从离散变量转换为连续变换。
因此,我们可以直接从重新排列这个方程开始,并将其极限从 -∞ 取为 ∞。

此时,在指数 e⁻⁻jw⁰ⁿt 中,⍵₀ 和 n 相乘为 ⍵,最终将系数 cn 从离散转换为连续。
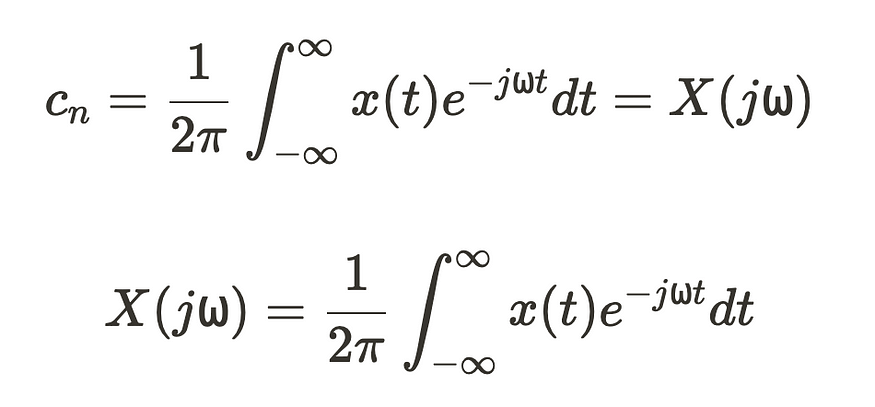
这里,x(t) 表示 f(t),因为它的极限为无穷大。X(j⍵) 是在频域中定义的信号,表征其在特定频率下的功率。
所以你有它。

从本质上讲,这种变换将连续和非周期信号x(t)从时域转换为频域X(j⍵)。
但请注意,虽然这种转换是非周期性的,并且可能看起来越来越有用......警告!
它是连续的!
在二进制 1 和 0 上运行的计算机将如何接收连续数据?
幸运的是,这就是我们有离散傅里叶变换的原因
六、离散傅里叶变换
离散傅里叶变换为使用计算机对真实数据进行采样和转换奠定了基础。
让我们以脑电图(EEG)为例。
在脑电图中,数据以特定时间间隔作为离散值输入,具体取决于采样率。鉴于此,计算机很容易处理这些数据,因为它在离散值上运行
离散傅里叶变换将允许我们使用在该脑电图中收集的离散数据,并将该数据从时域转换为频域,以便在计算机上进行更好的分析。
为了推导离散傅里叶变换,我们采用连续傅里叶变换,

并在 N 个样本的有限间隔内对其进行采样。
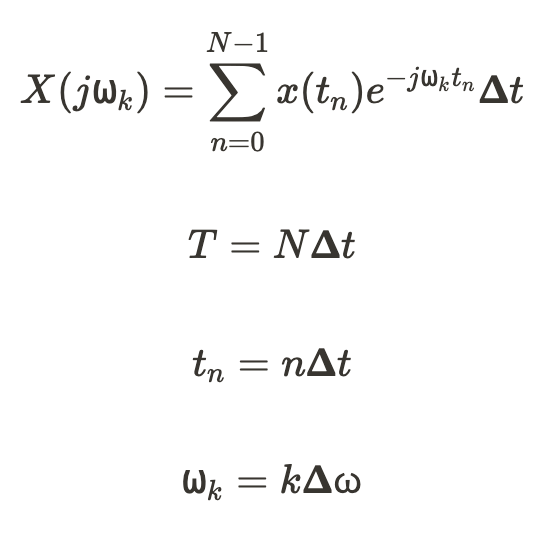
- 周期性 T 是总样本 (N) 和采样间隔 Δt 的乘积。
- 离散时间点 (tn) 是索引 n 和采样间隔 Δt 的乘积。
- ⍵,整体表示第 k 个频率分量处的频率 bin。
- ⍵k 表示 ⍵ 频率箱中第 n 个索引处的特定频率。
很酷,但 k 到底是从哪里来的???
井变量 k 表示第 k 个频率分量。在每个离散时间样本 n 处,我们将有 k 个构成信号的非周期频率分量。

不幸的是,如果我们有一个高值 N,计算机必须进行大量的计算,这可能会带来问题......我们稍后会谈到这一点。
因此,使用

我们可以将方程式改写为:
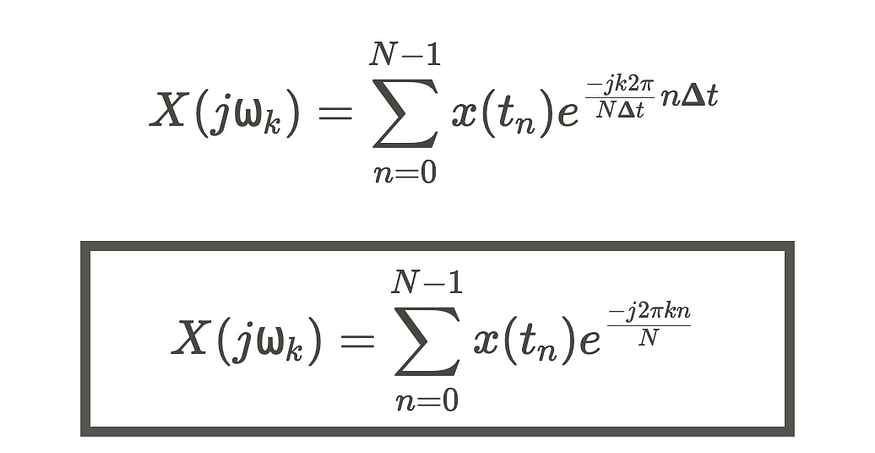
我们得到了 DFT。
但是等一下,我们还没有完成!
DFT 的方程可以简化,并通过所谓的统一根来表示。
从本质上讲,统一根是一个复数,当提高到第 n 个整数时,当 n 是正整数时,指数的结果是 1。
因此,我们可以用单位的第 N 根来表示我们的方程,
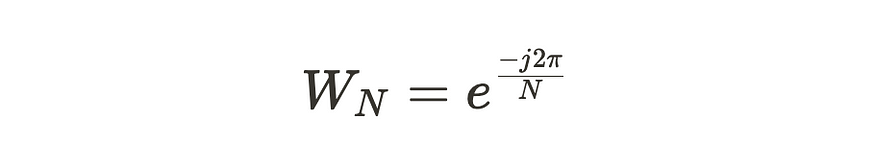
进一步简化为,
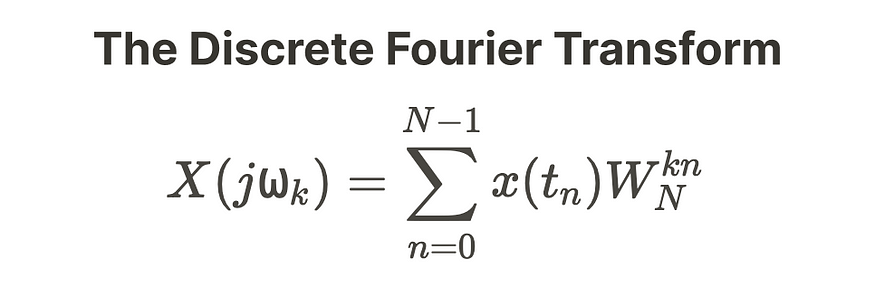
现在,如果你还记得我之前提到的,
“不幸的是,如果我们有一个高值的 N,计算机必须进行大量的计算,这可能会带来问题......我们稍后会讨论这个问题。
在计算信号的频谱/频域时,DFT可能被证明是无效的。
计算时间、负载和复杂性太多了!
原因如下。
让我们再看一下我们的DFT方程。


对于每个 k 值,我们必须处理 N-1 次计算。
如果我们再看一下早期的视觉效果,以获得更多的视角,

很明显,如果我们有一个更高的索引 N,我们将不得不处理每 N 个不断增加的 k 个计算量。
变量 N 还决定了我们的计算机将决定使用多少个索引。我们不仅要担心 k 个计算,还要担心 n。
因此,最终,当您同时考虑 k 和 n 时,您需要执行 N² 计算。
如果你听说过Big O Notation,你就会知道这很糟糕。
让我给你看看。
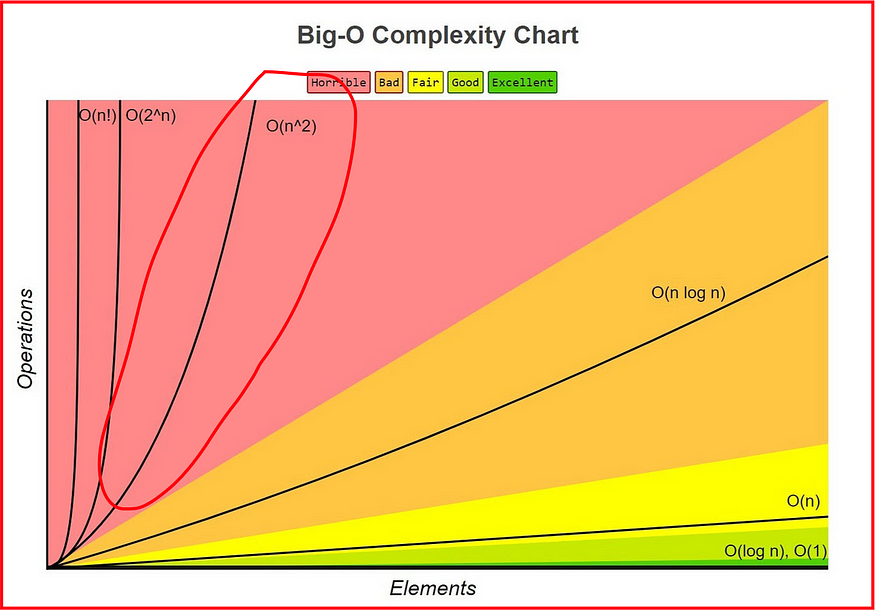
随着时间的流逝,随着我们值 N 的增加,我们的整体计算复杂度将呈指数级增长。
如果我们的数据集中有 3000 个采样数据,那么总共需要 9,000,000 次计算机操作才能遍历整个数据集。请记住,计算复杂性呈指数级增长。
与较低的 Big-O 复杂性相比,这是巨大的。
但这就是我们有快速傅里叶变换:)的原因。
七、快速傅里叶变换
因此,为了缓解 DFT 的计算复杂性随着 N 的增加呈指数级增长的问题,需要进行一些轻微的修改。
数学家约翰·图基(John Tukey)与约翰·肯尼迪(John F. Kennedy)总统进行了讨论,讨论了使用该国周围的传感器检测苏联核试验的可能性。
他意识到,为了利用这些传感器,他们需要一种计算复杂度较低的算法。
他们与James Cooley一起发表了一篇论文,概述了FFT的可用性,以便将计算复杂度从N²降低到nlog₂ n,这是一个极大的改进。

正如你所看到的,计算以更线性的方式增加,而不是指数增长。
这使得事情更加高效和可行,尤其是当我们有大量数据点需要计算时。
让我告诉你为什么。
让我们再看一下DFT。
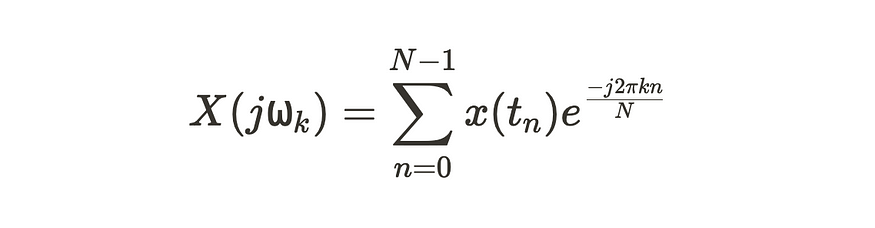
假设我们要计算第二个傅里叶系数 X(1)。

现在,假设我们还想计算第三个傅里叶系数 X(2)。
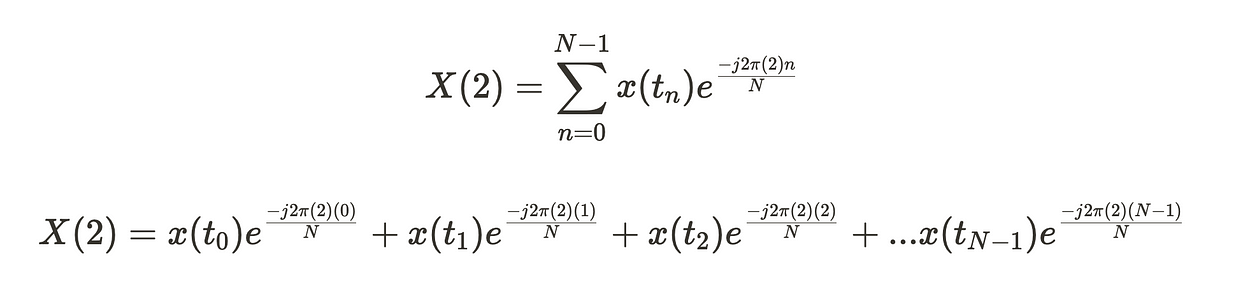
如果你没有注意到,第三个系数,其中 X(1),与第二个系数相同,其中 X(2)。

因此,最终,计算机不是计算相同的指数,在多个 k 值上两次产生相同的结果,而是使用 FFT 计算指数,然后将该指数存储在它的内存中以供将来访问。
这样可以提高计算速度并更好地利用计算资源。

DFT 矩阵
您可以看到,在 DFT 矩阵中重复 ⍵。
每个 ⍵,将仅使用 FFT 算法计算一次
在增加的 k 值上这样做,增加了每个 FFT 算法节省的计算资源量
还行。。。我们是怎么做到的?
好吧,FFT并不太复杂。将 FFT 视为一种更有效地计算 DFT 的算法。不是一个全新的公式。
让我们再看一下DFT。
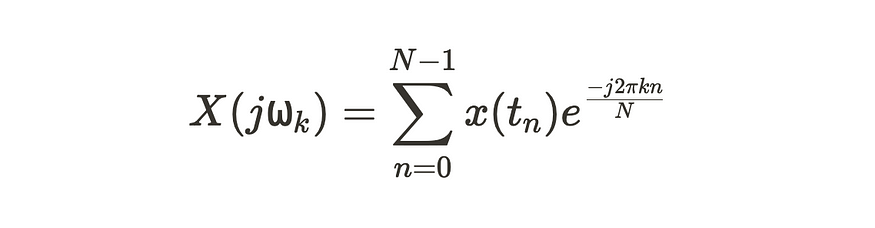
因此,这个方程可以通过除法 N/2 分为 2 个独立的序列。一个序列将包含所有偶数 n 个值,另一个序列将包含所有奇数值。
我们将序列称为 g(tn) 和 f(tn)。

鉴于此,DFT 可以分解为 2 个单独的求和。

从这里开始,我们可以进一步分解我们的求和。
让我们将下一个函数定义为 h(tn) 和 i(tn)。

每次我们将一个求和分成两个新的单独求和时,我们都会将计算 DFT 的运算总数减半。
从本质上讲,这是构成 FFT 算法的过程。
八、那又怎样
所有这些复杂的公式和算法有什么意义?所有这些转换都是我们为什么能够与复杂形式的数据进行交互的基本基础。
它是我们与之交互的各种过程和系统的重要工具,例如 X 射线、脑电图、电话、天气预报等等。
更重要的是,像这些转换这样的基础数学为创造新的和改进的技术让路,如脑机接口、量子计算、智能电网,甚至人工智能。

了解新兴技术背后的数学过程可以让您真正了解如何开始使用它们甚至改进它们。