leetcode刷题（javaScript）——堆相关场景题总结

堆是什么？堆都能用树表示，并且一般树的实现都是利用链表。平时使用的最多的是二叉堆，它可以用完全二叉树表示，二叉堆易于存储，并且便于索引。在堆的实现时注意：因为是数组，所以父子节点的关系就不需要特殊的结构去维护了，索引之前通过计算就可以得到，省掉了很多麻烦，如果是链表结构，就会复杂很多。

在JavaScript刷题中，堆（Heap）通常用于解决一些需要高效处理优先级的问题，例如找出最大或最小的K个元素、实现优先队列等。堆在刷题中的应用场景包括但不限于以下几个方面：

找出最大或最小的K个元素：通过维护一个大小为K的最大堆或最小堆，可以快速找出数组中最大或最小的K个元素。
合并K个有序数组：可以使用堆来合并K个有序数组，实现高效的合并操作。
实现优先队列：堆可以用于实现优先队列，保证队列中优先级高的元素先出队。

数组存储二叉堆

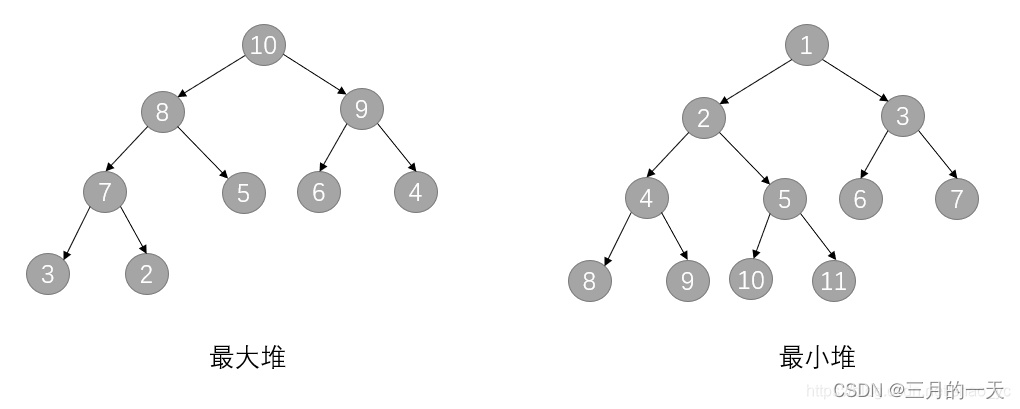
二叉堆是一种完全二叉树，分为最小堆和最大堆两种类型。用数组存储二叉堆，完全二叉树要求叶子节点从左往右填满，才能开始填充下一层。

二叉堆：二叉堆是一种完全二叉树，通常使用数组来表示。在最小堆中，父节点的值小于或等于其子节点的值；在最大堆中，父节点的值大于或等于其子节点的值。
最小堆：在最小堆中，父节点的值小于或等于其子节点的值。根节点是堆中的最小值。
最大堆：在最大堆中，父节点的值大于或等于其子节点的值。根节点是堆中的最大值。

注：完全二叉树和满二叉树不同，完全二叉树允许叶子节点不铺满。

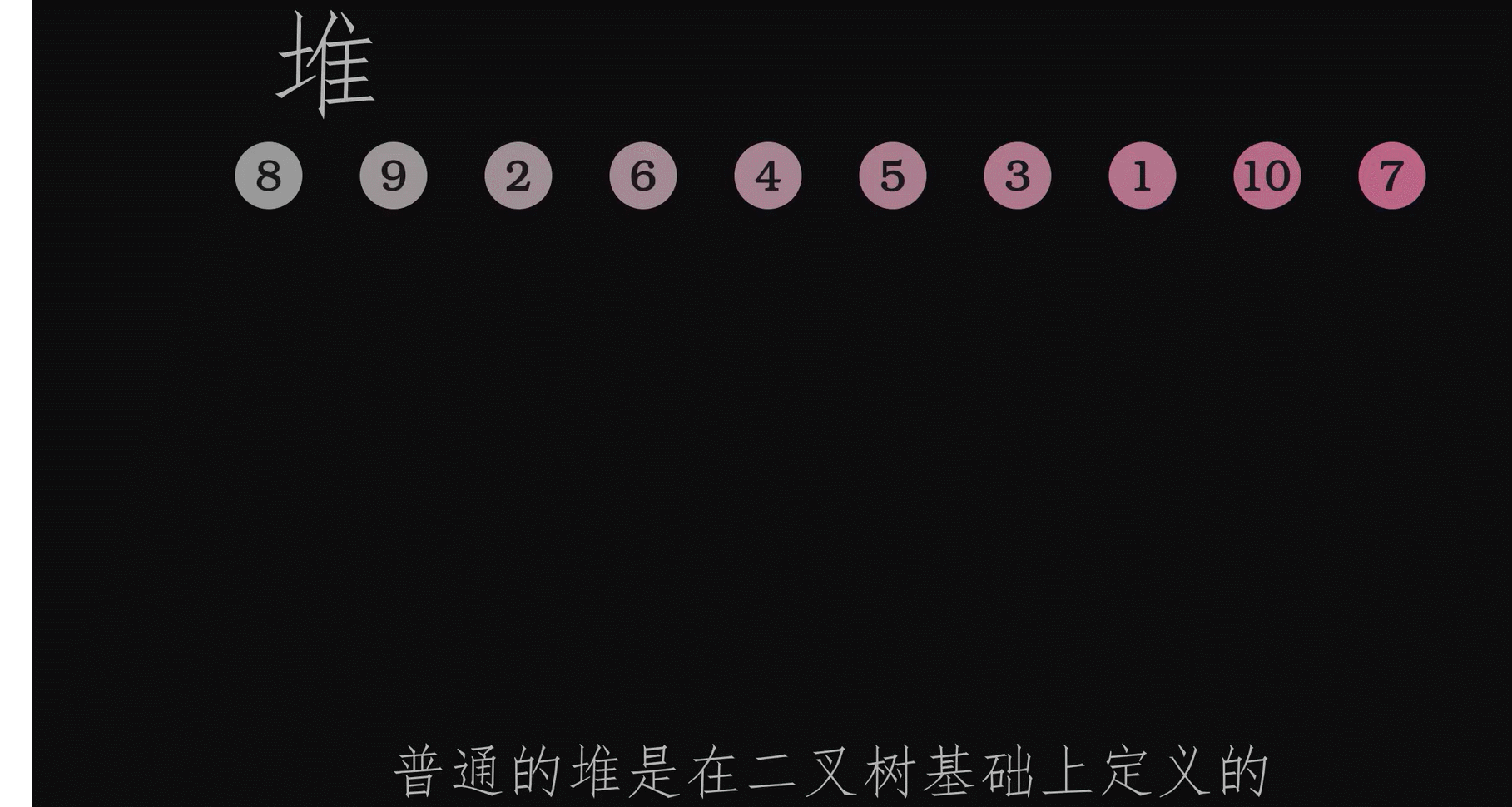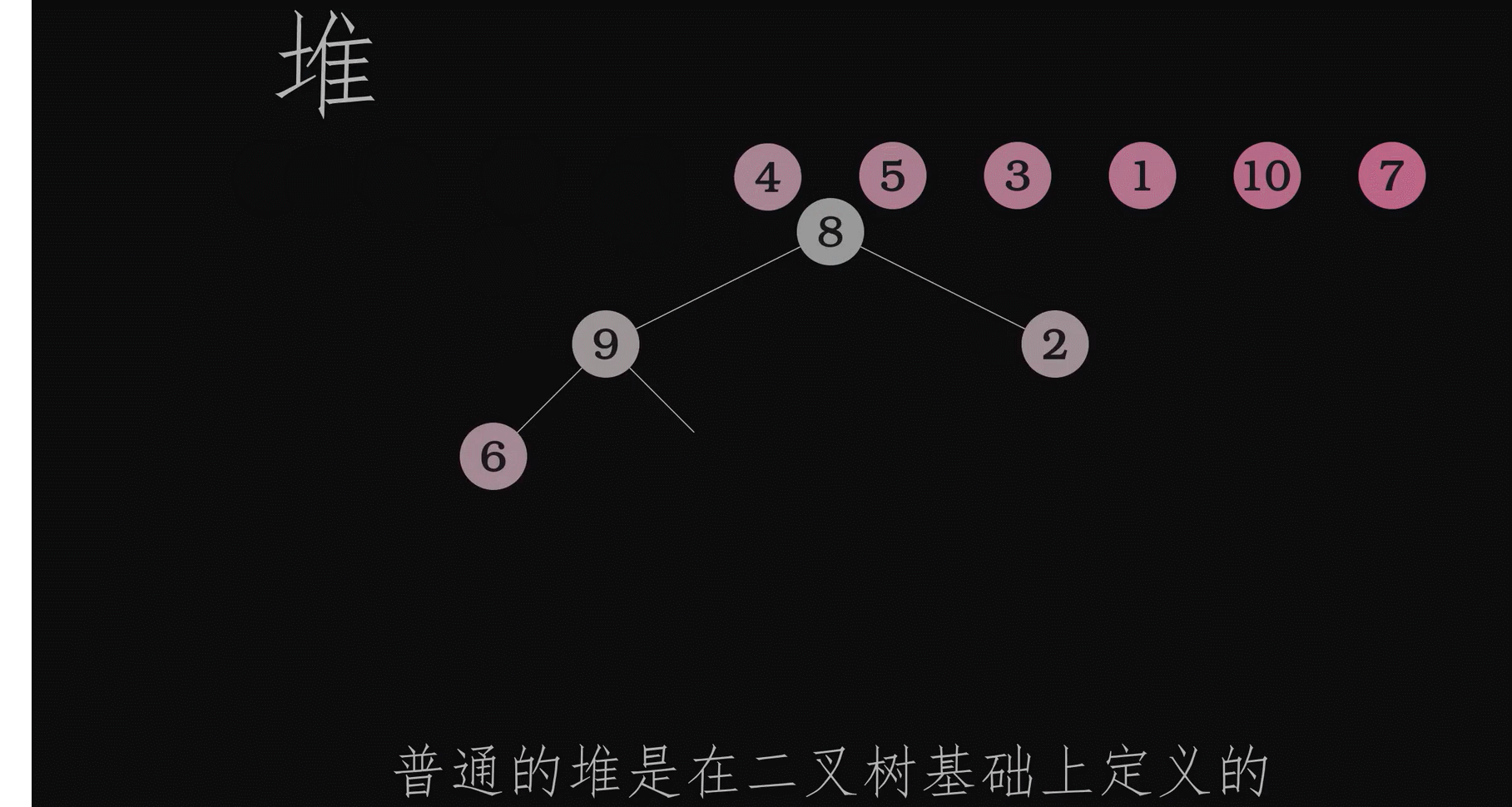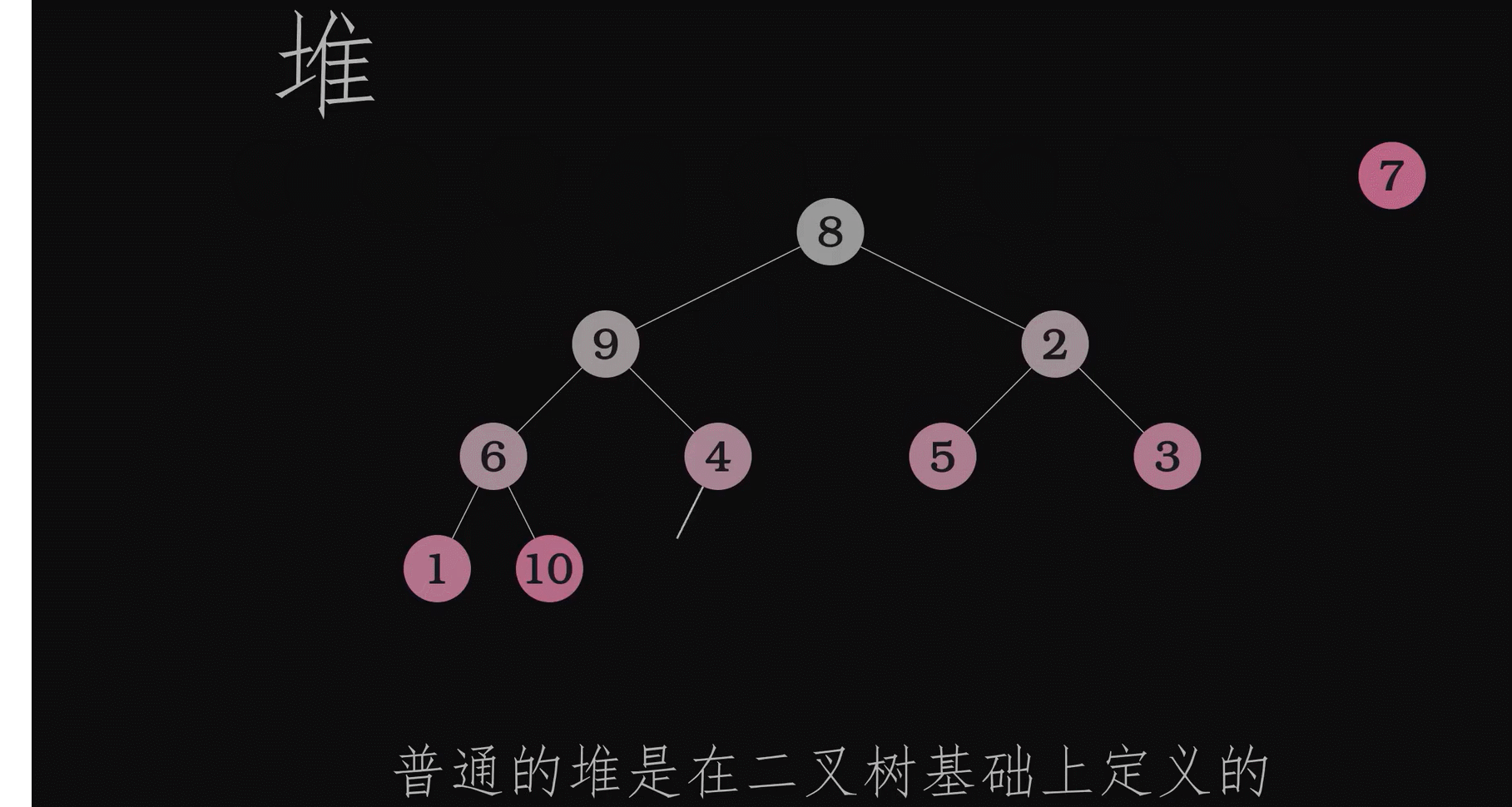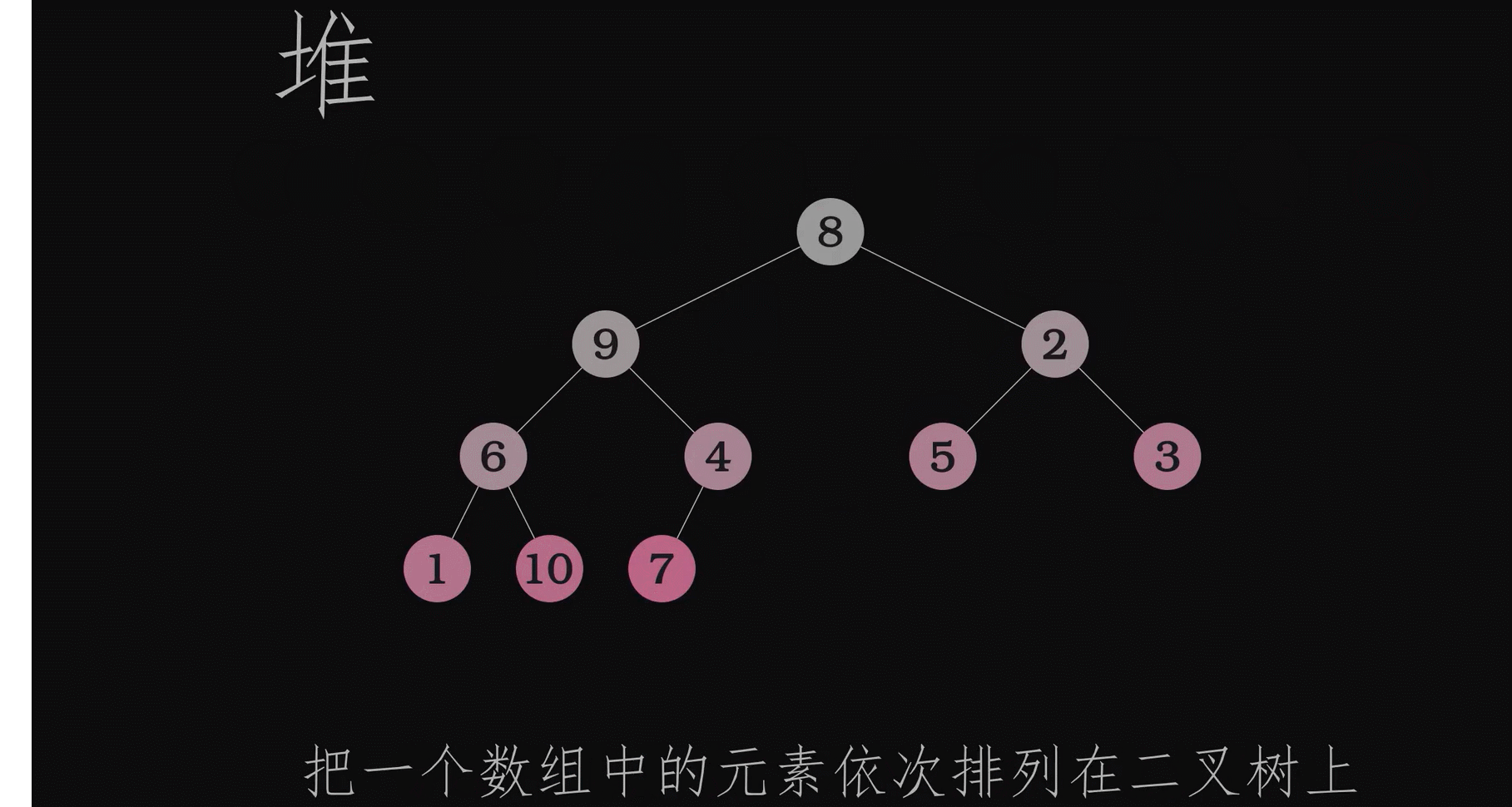
动画演示创建堆的过程

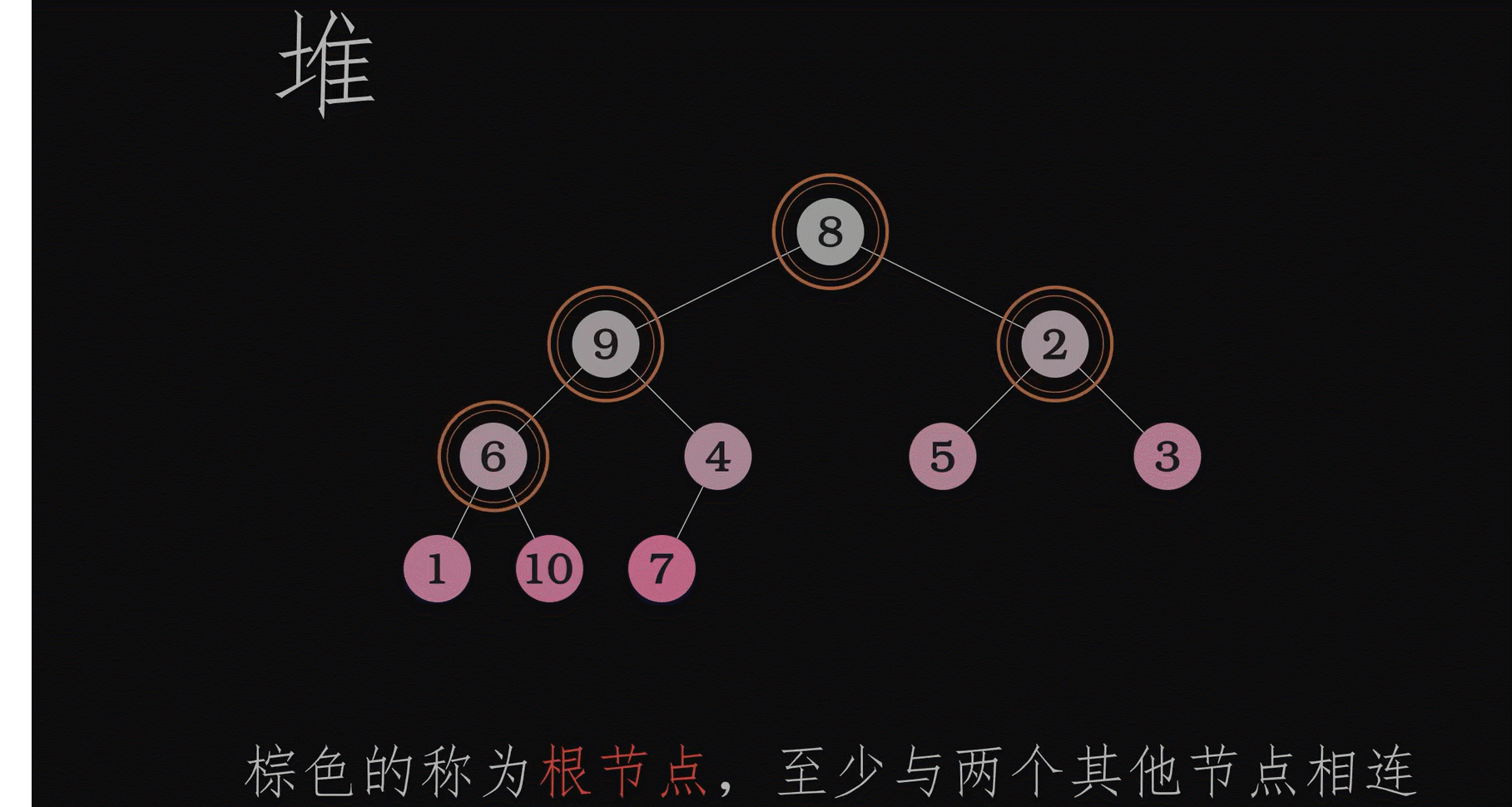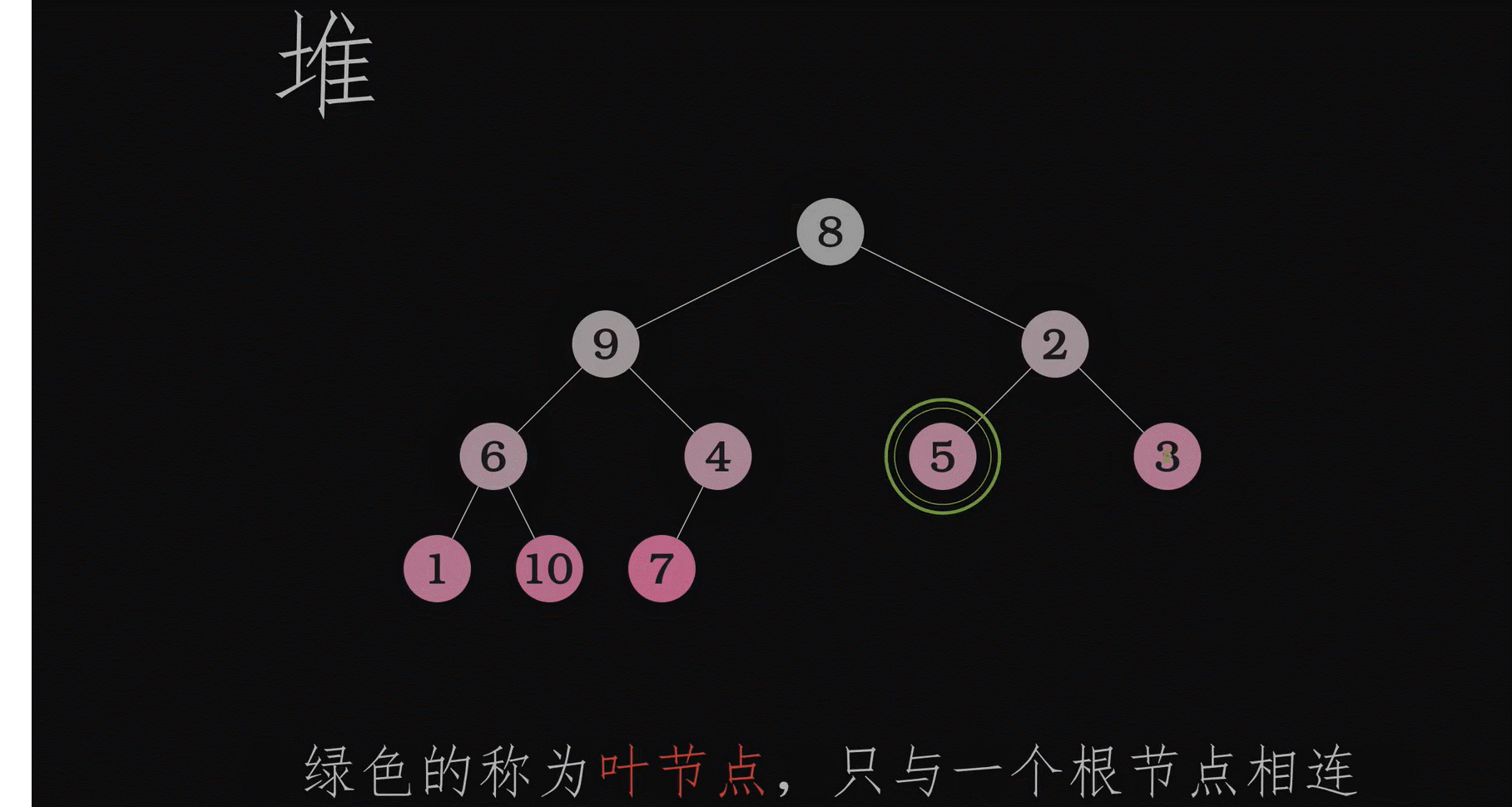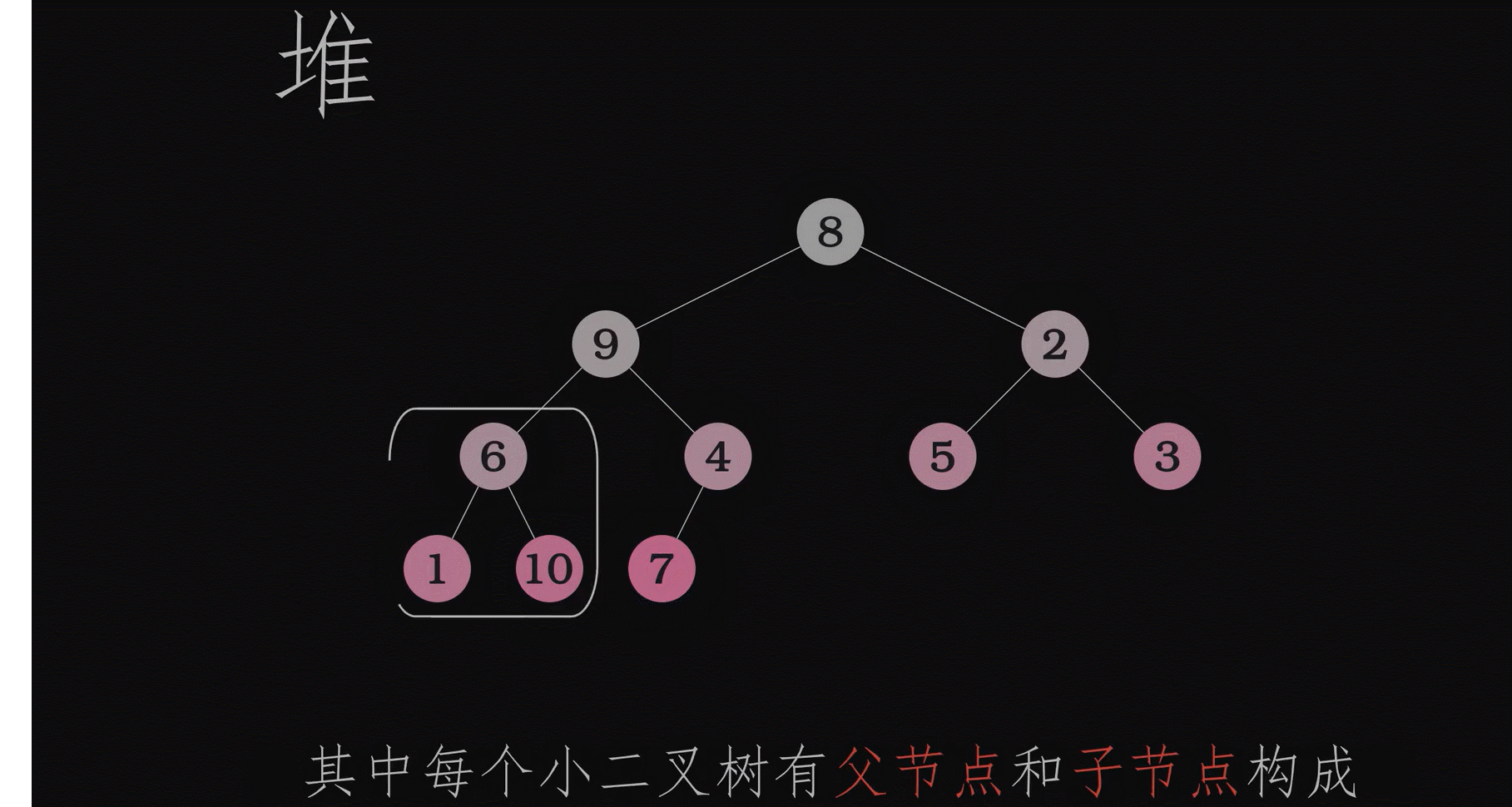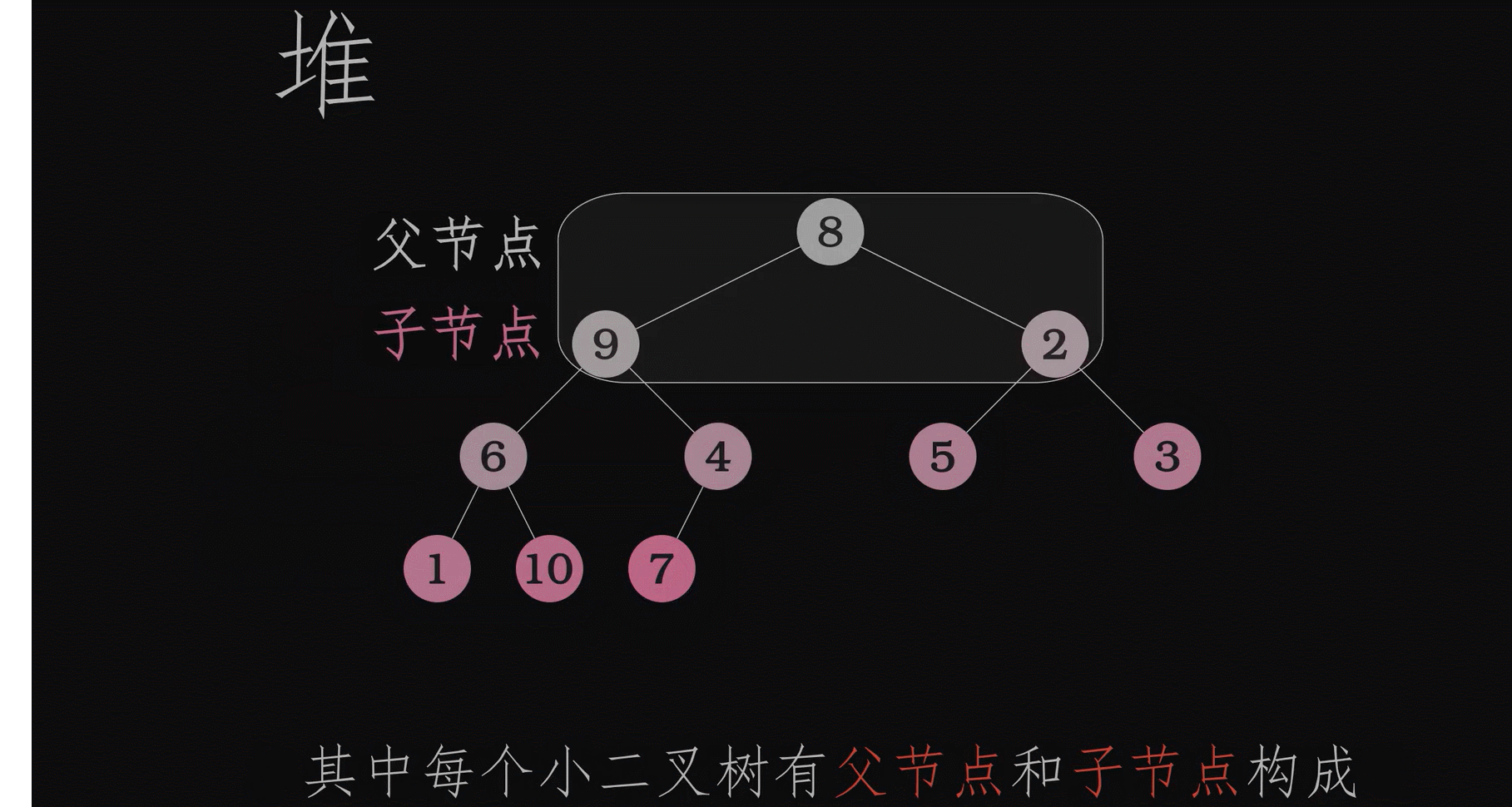
同一组数据最小堆和最大堆是唯一的吗？

同一组数据的最小堆或最大堆不是唯一的。以最小堆为例：最小堆是一种特殊的二叉堆，它满足以下两个性质：

父节点的值小于或等于其子节点的值。
堆中任意节点的子树也是一个最小堆。

由于最小堆只要满足上述性质即可，因此对于同一组数据，可以有多种不同的最小堆表示方式。这是因为在构建最小堆的过程中，可以选择不同的节点作为根节点，从而得到不同的堆结构。

所以，同一组数据的最小堆并不是唯一的，可以有多种不同的表示方式。

如何找到节点i父节点和子节点呢？

二叉堆在数组是按层次遍历进行存储的，从上至下，从左至右。因此子节点的index要大于父节点的index。在二叉堆中，可以通过以下方式计算父节点和子节点的索引：

父节点索引计算：对于节点i，其父节点的索引为(i-1)/2。
左子节点索引计算：对于节点i，其左子节点的索引为2*i+1。
右子节点索引计算：对于节点i，其右子节点的索引为2*i+2。

如何删除节点？

在删除一个元素之后，整体往前移动是比较费时的，这也是随机存储结构的短板。因此，堆在删除元素的时候是把最后一个叶子节点补充到树根节点。在通过节点移动将堆调整为最小堆或最大堆。

如何通过js构建最大堆

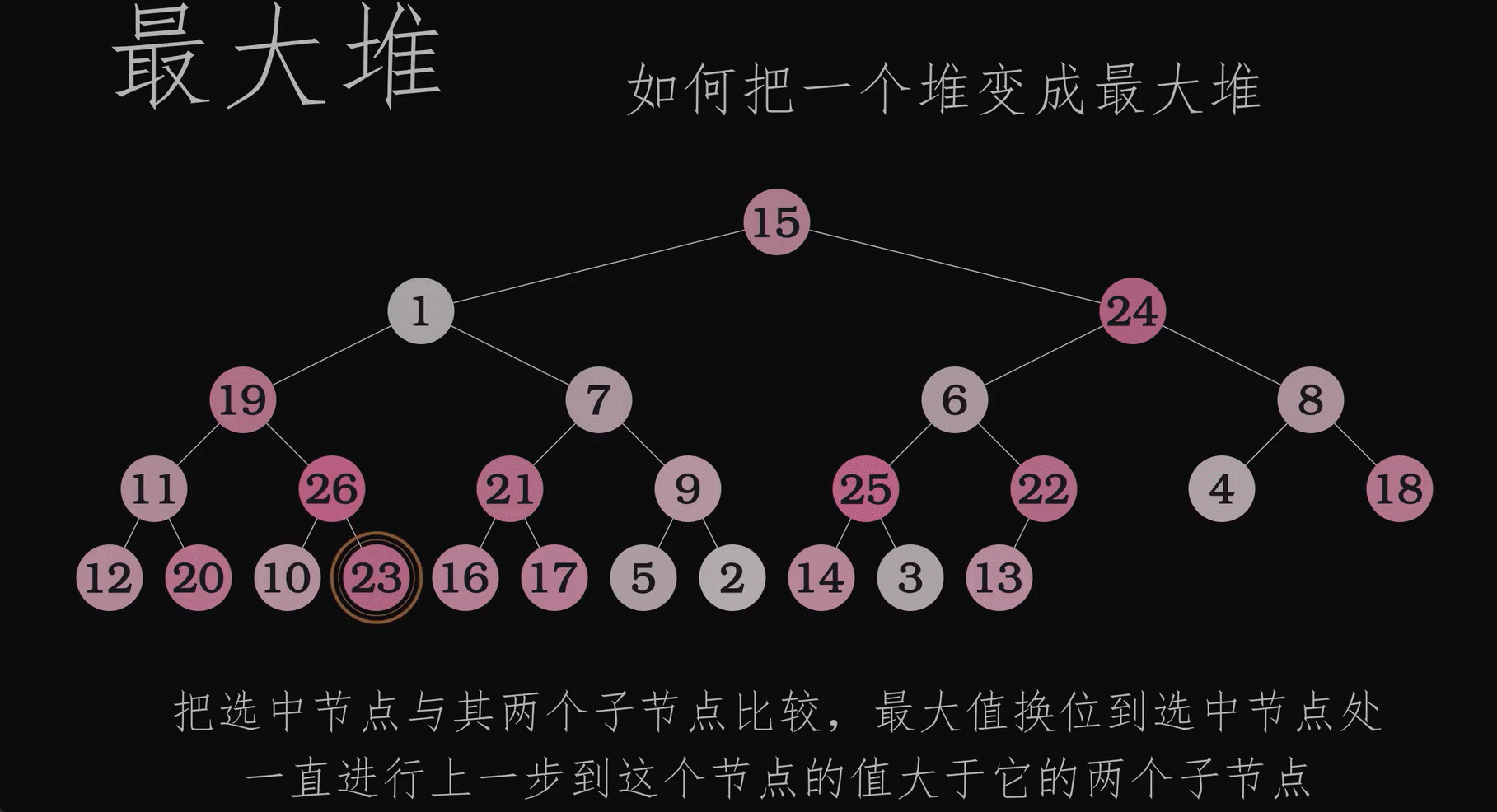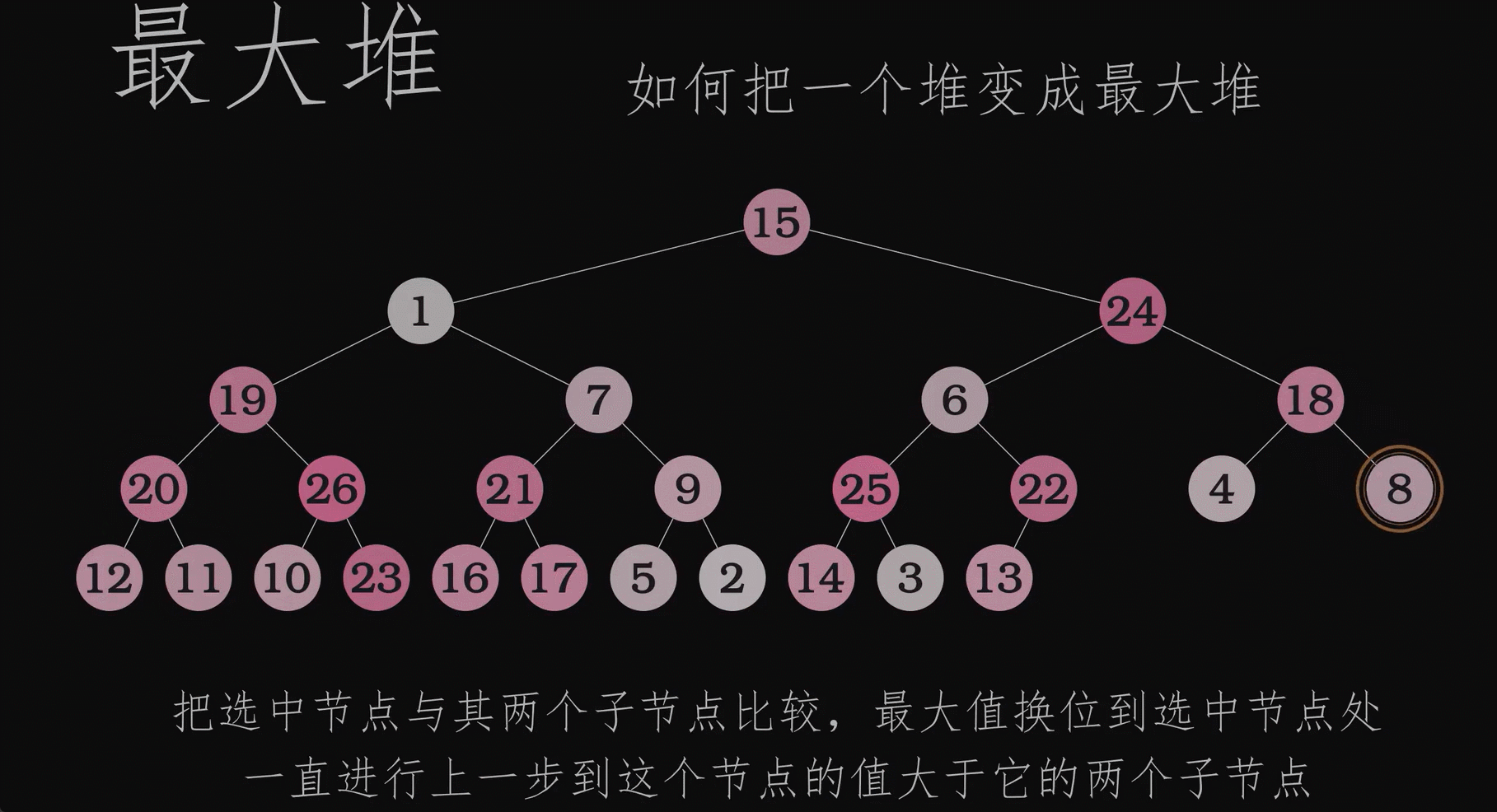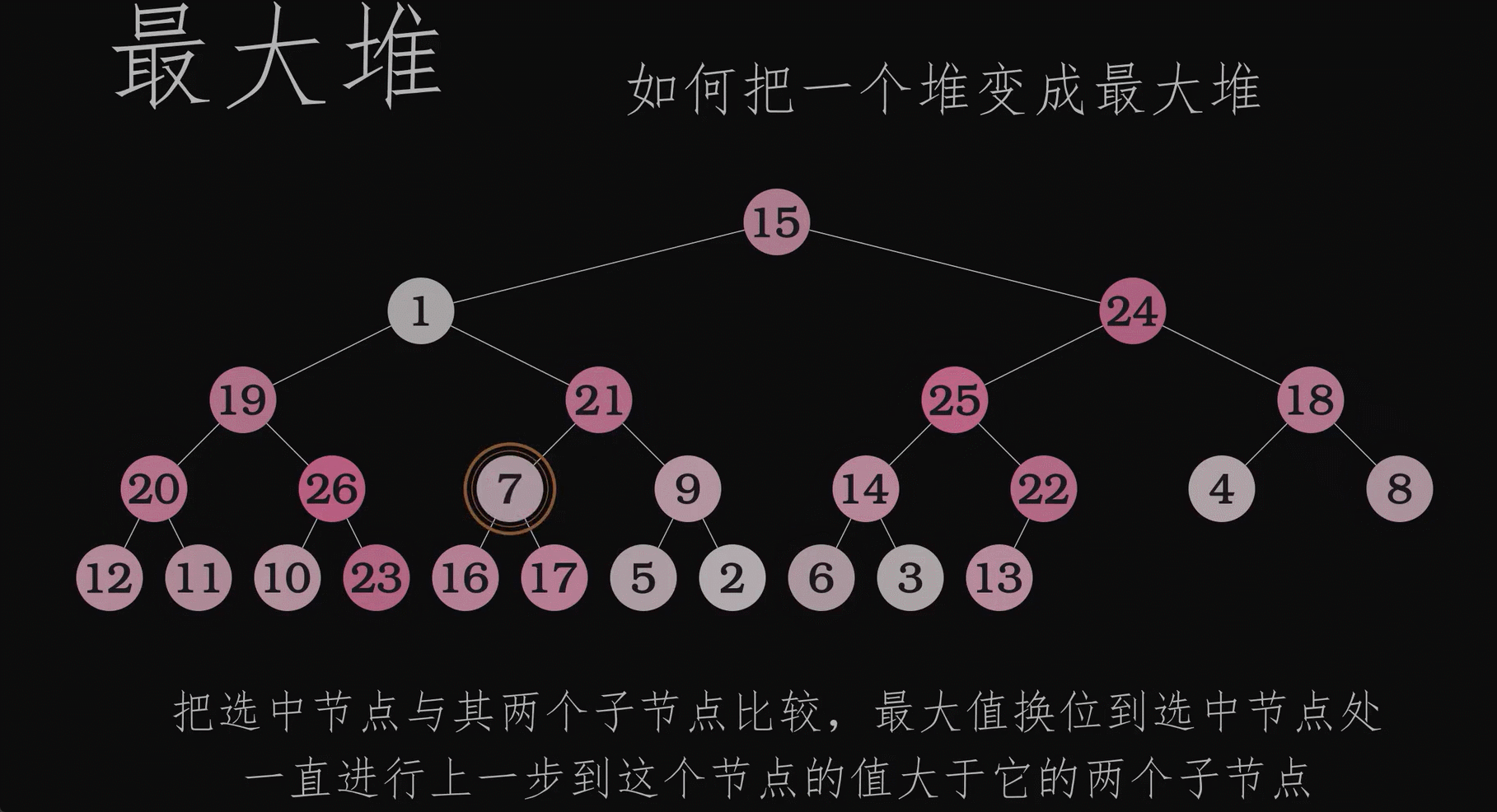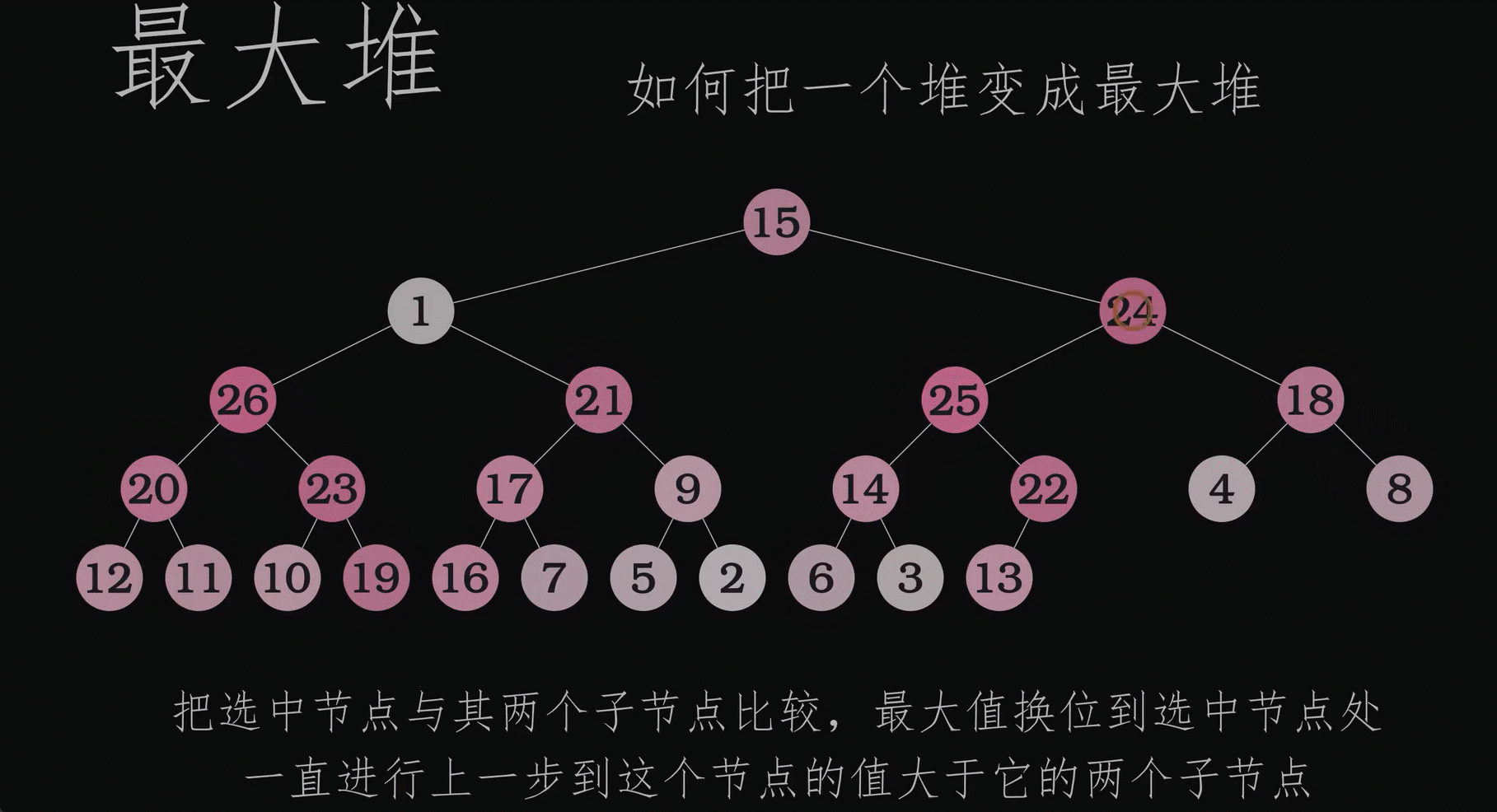
首先构造器得有吧，创建一个空的heap数组；

其次将获取父节点index、左右子节点index、堆大小size、栈顶元素获取、两节点交换这些简单的辅助函数写一下；

主函数insert插入节点：每次从heap的尾部也就是最后一个叶子节点插入，插进去的叶子节点得向上找它的位置吧，写一个up方法，找到插入节点位置；

up方法实现：找到节点的父元素，看父元素是否比自己小，如果小的换就交换，并且递归up方法，直到所有元素都调整好。

删除节点pop方法：这里依然将最后节点移到第一个跟节点，此时根节点一定是最小的，不符合最大堆规则，所以调整跟节点向下移动，写一个down方法移动根节点。这里注意堆的size如果等于1直接删除而不用移动节点。

down方法实现：找到根的左右子节点，选择比根大的节点进行交换，并递归down方法，直到所有节点都调整好。

交换节点swap可以使用数组解构进行交换，而不用单独定义中间值。

class MaxHeap {constructor() {this.heap = [];}//获取父元素下标getParentIndex(index) {return Math.floor((index - 1) / 2);}//获取左子树下标getLeftIndex(index) {return 2 * index + 1;}//获取右子树下标getRightIndex(index) {return 2 * index + 2;}//获取堆大小size() {return this.heap.length;}//获取堆顶元素peek() {return this.heap[0];}//交换节点swap(id1, id2) {[this.heap[id2], this.heap[id1]] = [this.heap[id1], this.heap[id2]];}//插入节点insert(value) {this.heap.push(value);this.up(this.size() - 1);}//删除节点pop() {let last = this.heap.pop();if (this.size() === 0) return;this.heap[0] = last;this.down(0);}//向上移动节点up(index) {const parentIndex = this.getParentIndex(index);if (this.heap[index] > this.heap[parentIndex]) {this.swap(parentIndex, index);this.up(parentIndex);}}//向下移动节点down(index) {const leftIndex = this.getLeftIndex(index);const rightIndex = this.getRightIndex(index);let smallIndex = index;if (leftIndex < this.size() &&this.heap[leftIndex] > this.heap[smallIndex]) {smallIndex = leftIndex;}if (rightIndex < this.size() &&this.heap[rightIndex] > this.heap[smallIndex]) {smallIndex = rightIndex;}if (smallIndex != index) {this.swap(smallIndex, index);this.down(smallIndex);}}
}

这里让根节点从左右节点中与最小的节点进行交换。注意减少交换次数，避免多次递归

如何通过js构建最小堆

与创建最小堆类似。创建堆，往堆里新增元素，删除堆顶，获取堆的父节点下标，获取堆左右子节点下标

代码示例

class MinHeap {constructor() {this.heap = [];}getParentIndex(index) {return Math.floor((index - 1) / 2);}getLeftIndex(index) {return index * 2 + 1;}getRightIndex(index) {return index * 2 + 2;}swap(i1, i2) {[this.heap[i1], this.heap[i2]] = [this.heap[i2], this.heap[i1]];}//往堆最后添加节点，触发元素上移//当前元素与其跟节点进行比较如果大于其跟节点与根节点进行交换，重复操作up(index) {//如果是0就不移动if (index == 0) return;//获取父元素const parentIndex = this.getParentIndex(index);if (this.heap[parentIndex] > this.heap[index]) {this.swap(parentIndex, index);//对交换后parentIndex继续向上递归this.up(parentIndex);}}//从堆顶删除元素时，将子节点移到堆顶，触发元素下移down(index) {const leftIndex = this.getLeftIndex(index);const rightIndex = this.getRightIndex(index);let smallIndex = index;//左子树小于根节点，交换左子树与根if (leftIndex < this.size() &&this.heap[leftIndex] < this.heap[smallIndex]) {smallIndex = leftIndex;}//同理，右子树小于根节点，交换右子树与根if (rightIndex < this.size() &&this.heap[rightIndex] < this.heap[smallIndex]) {smallIndex = rightIndex;}if (smallIndex != index) {this.swap(smallIndex, index);this.down(smallIndex);}}//往堆里增加元素insert(value) {this.heap.push(value);this.up(this.heap.length - 1);}//将堆顶元素弹出//删除节点pop() {let last = this.heap.pop();if (this.size() === 0) return;this.heap[0] = last;this.down(0);}//获取堆顶peek() {return this.heap[0];}//获取堆大小size() {return this.heap.length;}
}

215. 数组中的第K个最大元素

解决数组中的第K个最大元素问题时，通常使用最小堆来实现。通过维护一个大小为K的最小堆，可以在O(NlogK)的时间复杂度内找到数组中的第K个最大元素。

但是题目最近新增了一个要求：就是必须让算法的时间复杂度控制在O(n)，当K很大时使用堆有可能会超出时间复杂度，所以要减少不必要的交换移动。

直到今天（2024.3.14）使用堆排序仍然可以跑通全部案例。

注：官方给的快速选择，甚至是"三数取中"的方法来选择基准值也都无法达到时间复杂度，会在第40/41个案例卡住。

使用最小堆获取数组中第K个最大元素的思路：

初始化一个大小为K的最小堆：将数组中的前K个元素放入最小堆中。
遍历数组剩余元素：从第K+1个元素开始遍历数组，对于每个元素，如果大于最小堆的堆顶元素（堆中最小的元素），则将该元素加入最小堆，并移除堆顶元素。
返回堆顶元素：遍历完成后，最小堆的堆顶元素即为数组中的第K个最大元素。

使用最小堆的优势在于可以保持堆的大小为K，只需维护K个元素，避免了对整个数组进行排序或维护大堆的复杂度。

class MinHeap {constructor() {this.heap = [];}getParentIndex(index) {return Math.floor((index - 1) / 2);}getLeftIndex(index) {return index * 2 + 1;}getRightIndex(index) {return index * 2 + 2;}swap(i1, i2) {[this.heap[i1], this.heap[i2]] = [this.heap[i2], this.heap[i1]];}//往堆最后添加节点，触发元素上移//当前元素与其跟节点进行比较如果大于其跟节点与根节点进行交换，重复操作up(index) {//如果是0就不移动if (index == 0) return;//获取父元素const parentIndex = this.getParentIndex(index);if (this.heap[parentIndex] > this.heap[index]) {this.swap(parentIndex, index);//对交换后parentIndex继续向上递归this.up(parentIndex);}}//从堆顶删除元素时，将子节点移到堆顶，触发元素下移down(index) {const leftIndex = this.getLeftIndex(index);const rightIndex = this.getRightIndex(index);let smallIndex = index;//左子树小于根节点，交换左子树与根if (leftIndex < this.size() && this.heap[leftIndex] < this.heap[smallIndex]) {smallIndex = leftIndex;}//同理，右子树小于根节点，交换右子树与根if (rightIndex < this.size() && this.heap[rightIndex] < this.heap[smallIndex]) {smallIndex = rightIndex;}if (smallIndex != index) {this.swap(smallIndex, index);this.down(smallIndex);}}//往堆里增加元素insert(value) {this.heap.push(value);this.up(this.heap.length - 1);}//将堆顶元素弹出//删除节点pop() {let last = this.heap.pop();if (this.size() === 0) return;this.heap[0] = last;this.down(0);}//获取堆顶peek() {return this.heap[0];}//获取堆大小size() {return this.heap.length;}
}
// 寻找第 k 个最大的元素
var findKthLargest = function (nums, k) {let minHeap = new MinHeap();nums.forEach(item => {minHeap.insert(item);if (minHeap.size() > k) {//每次pop的是栈顶，及k+1个元素中最小的minHeap.pop();}})return minHeap.peek();
};

算法可以通过全部的41个测试用例

703. 数据流中的第 K 大元素

设计一个找到数据流中第 k 大元素的类（class）。注意是排序后的第 k 大元素，不是第 k 个不同的元素。

请实现 KthLargest 类：

KthLargest(int k, int[] nums) 使用整数 k 和整数流 nums 初始化对象。
int add(int val) 将 val 插入数据流 nums 后，返回当前数据流中第 k 大的元素。

思路：也是用最小堆来实现，最小堆前面已经介绍过堆的插入删除，直接将创建堆对象的类拿来用即可。

动态构建一个长度为k的最小堆，对顶即第k大的的元素。因为比k小的元素都被pop出去了

/*** @param {number} k* @param {number[]} nums*/
var KthLargest = function (k, nums) {//构建一个k个长度的最小堆this.k = k;this.minHeap = new MinHeap();// 初始化最小堆for (let num of nums) {this.add(num);}
};/** * @param {number} val* @return {number}*/
KthLargest.prototype.add = function (val) {this.minHeap.insert(val);while (this.minHeap.size() > this.k) {this.minHeap.pop();}return this.minHeap.peek();
};/*** Your KthLargest object will be instantiated and called as such:* var obj = new KthLargest(k, nums)* var param_1 = obj.add(val)*/
class MinHeap {constructor() {this.heap = [];}getParentIndex(index) {return Math.floor((index - 1) / 2);}getLeftIndex(index) {return index * 2 + 1;}getRightIndex(index) {return index * 2 + 2;}swap(i1, i2) {[this.heap[i1], this.heap[i2]] = [this.heap[i2], this.heap[i1]];}//往堆最后添加节点，触发元素上移//当前元素与其跟节点进行比较如果大于其跟节点与根节点进行交换，重复操作up(index) {//如果是0就不移动if (index == 0) return;//获取父元素const parentIndex = this.getParentIndex(index);if (this.heap[parentIndex] > this.heap[index]) {this.swap(parentIndex, index);//对交换后parentIndex继续向上递归this.up(parentIndex);}}//从堆顶删除元素时，将子节点移到堆顶，触发元素下移down(index) {const leftIndex = this.getLeftIndex(index);const rightIndex = this.getRightIndex(index);let smallIndex = index;//左子树小于根节点，交换左子树与根if (leftIndex < this.size() &&this.heap[leftIndex] < this.heap[smallIndex]) {smallIndex = leftIndex;}//同理，右子树小于根节点，交换右子树与根if (rightIndex < this.size() &&this.heap[rightIndex] < this.heap[smallIndex]) {smallIndex = rightIndex;}if (smallIndex != index) {this.swap(smallIndex, index);this.down(smallIndex);}}//往堆里增加元素insert(value) {this.heap.push(value);this.up(this.heap.length - 1);}//将堆顶元素弹出//删除节点pop() {let last = this.heap.pop();if (this.size() === 0) return;this.heap[0] = last;this.down(0);}//获取堆顶peek() {return this.heap[0];}//获取堆大小size() {return this.heap.length;}
}

1046. 最后一块石头的重量

有一堆石头，每块石头的重量都是正整数。

每一回合，从中选出两块 最重的 石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块石头。返回此石头的重量。如果没有石头剩下，就返回 0。

思想：构建一个最大堆，从堆顶取两个值分别为y,x判断如果y>x则将y-x放入堆中并将堆调整为最大堆。递归直到堆长度小于2。如果堆里还有值则返回堆顶元素，否则为0

/*** @param {number[]} stones* @return {number}*/
var lastStoneWeight = function (stones) {if (stones.length == 1) return stones[0];let maxHeap = new MaxHeap();stones.forEach((item) => maxHeap.insert(item));while (maxHeap.size() > 1) {let y = maxHeap.peek();maxHeap.pop();let x = maxHeap.peek();maxHeap.pop();if (y > x) {maxHeap.insert(y - x);}}return maxHeap.size() ? maxHeap.peek() : 0;
};
/*** @param {number[]} stones* @return {number}*/
var lastStoneWeight = function (stones) {if (stones.length == 1) return stones[0];let maxHeap = new MaxHeap();stones.forEach((item) => maxHeap.insert(item));while (maxHeap.size() > 1) {let y = maxHeap.peek();maxHeap.pop();let x = maxHeap.peek();maxHeap.pop();if (y > x) {maxHeap.insert(y - x);}}return maxHeap.size() ? maxHeap.peek() : 0;
};
class MaxHeap {constructor() {this.heap = [];}//获取父元素下标getParentIndex(index) {return Math.floor((index - 1) / 2);}//获取左子树下标getLeftIndex(index) {return 2 * index + 1;}//获取右子树下标getRightIndex(index) {return 2 * index + 2;}//获取堆大小size() {return this.heap.length;}//获取堆顶元素peek() {return this.heap[0];}//交换节点swap(id1, id2) {[this.heap[id2], this.heap[id1]] = [this.heap[id1], this.heap[id2]];}//插入节点insert(value) {this.heap.push(value);this.up(this.size() - 1);}//删除节点pop() {let last = this.heap.pop();if (this.size() === 0) return;this.heap[0] = last;this.down(0);}//向上移动节点up(index) {const parentIndex = this.getParentIndex(index);if (this.heap[index] > this.heap[parentIndex]) {this.swap(parentIndex, index);this.up(parentIndex);}}//向下移动节点down(index) {const leftIndex = this.getLeftIndex(index);const rightIndex = this.getRightIndex(index);let smallIndex = index;if (leftIndex < this.size() &&this.heap[leftIndex] > this.heap[smallIndex]) {smallIndex = leftIndex;}if (rightIndex < this.size() &&this.heap[rightIndex] > this.heap[smallIndex]) {smallIndex = rightIndex;}if (smallIndex != index) {this.swap(smallIndex, index);this.down(smallIndex);}}
}