在实际工作中,我们经常会遇到这样一类问题:给机器输入大量的特征数据,并期望机器通过学习找出数据存在的某种共性特征、结构或关联。这类问题被称为“非监督学习”问题。这篇文章我就来聚焦非监督学习中的其中一个任务——聚类
例如在数字营销中,可以基于用户在线浏览习惯、点击历史、社交媒体行为等多维度数据进行聚类分析。发现几个主要的用户群体,比如“科技发烧友”、“健身爱好者”和“亲子家庭”等。对于每一个细分群体,企业可以设计并推送定制化的广告内容,从而提高广告效果和转化率。
一、聚类是什么?
我之前的文章中提到的支持向量机SVM、逻辑回归和决策树机器学习算法都是用于分类问题。即更具一些已经给定类别标签的样本,训练某种分类器,使得他们能够对类别未知的样本进行分类。与分类问题不同,聚类是在事先不知道任何样本的类别标签的情况下,通过数据之间的内在关系把样本划分为若干类别,使得同类样本之间相似度高,不同类之间相似度低。
总结起来对聚类下个定义:聚类是机器学习中的一种无监督学习方法,它旨在通过相似性或距离度量将物理或抽象对象的集合自动划分为多个类别或簇。
二、什么K-means算法?
K-means算法又叫做K均值算法,他是一种迭代的无监督聚类方法,通过将数据集中的样本点划分到不同的K个簇中,来寻找数据的内在关联。
(1)K-means算法的目标
- 将数据集划分为K个簇,使得每个簇内的数据点彼此相似度较高,而不同的簇之间的数据点差异较大。
- 簇内的相似性通常基于欧式距离,即簇内所有数据点与该簇中心点的距离之和尽可能的小。
(2)如何判断两个样本相似?
通过两点之间的欧式空间中的距离,公式如下:
三、简述K-means算法的具体步骤
(1)初始化
将数据样本先进行预处理(归一化、离群点处理等等),然后随机选取K个质心(簇中心),记为
定义代价函数,常用的代价函数是各个样本距离所属簇中心点的误差平方和:
| 符号 | 解释 |
| J | 代价函数 |
| 指第 | |
| 指 | |
| 指 | |
| m | 是样本总数 |
| 第k个簇的中心点(质心) |
(2)分配阶段
计算数据集中每个数据点到K个质心的距离,并将每个数据点分配给最近的质心所在的簇。
- 每个样本
将其分配的距离最近的簇,公式如下:
(3)更新阶段
根据每个簇中新分配的数据点重新计算簇的质心,通常是取簇内所有数据点坐标的平均值作为新的质心。
- 每个类簇k,重新计算该类簇的中心,公式如下:
举例说明:比如有4个样本他们的坐标是
,他们的质心计算可以拆解为,先计算x轴的平均值
,再计算y轴的平均值
,新质点
的位置就是
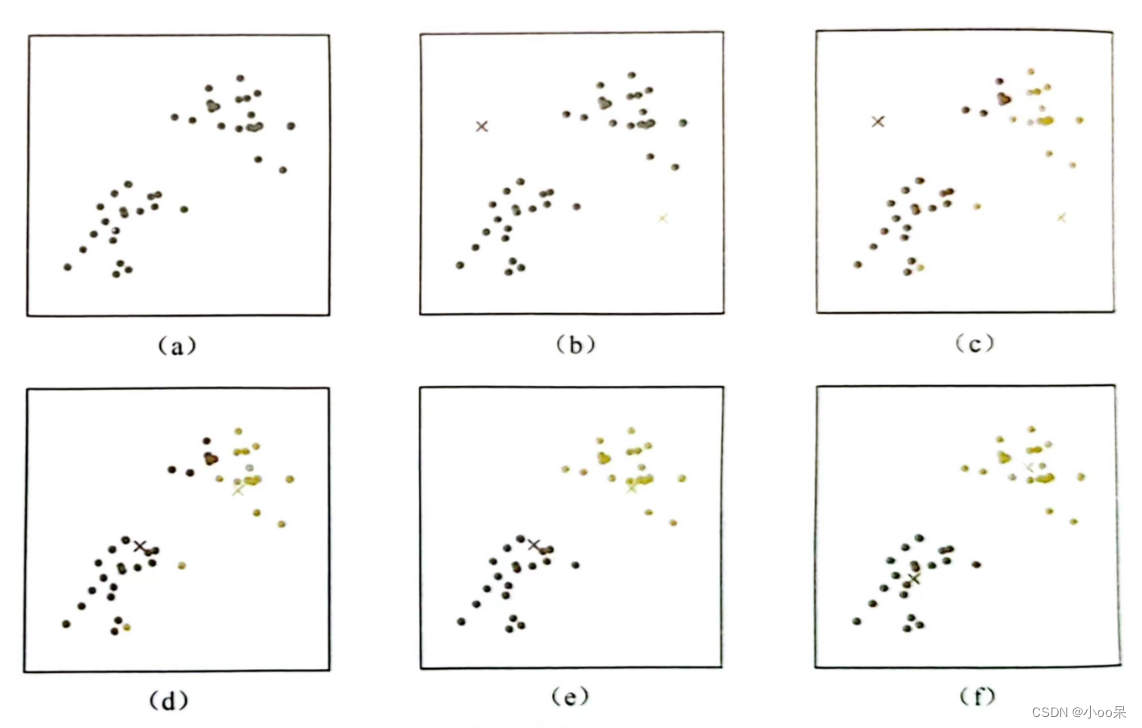
(4)迭代优化
重复步骤2和步骤3,直到满足终止条件为止,常见的终止条件包括预设的最大迭代次数或者质心移动的距离小于某个阈值,或者簇间的质心不再显著改变。
三、K-means算法的优缺点是什么
(1)优点
算法流程直观,易于理解与实现,适合大规模数据集处理。对于大数据集有相对较低的时间复杂度(尤其是在维度不太高时)。可以通过并行化技术在分布式环境下加速运行。在适当初始化的情况下,算法通常能快速收敛到局部最优解。得到的聚类结果具有明确的几何意义,每个簇有一个中心点,可以直观地解释和可视化。
(2)缺点
- 需要预设K值:需要预先确定簇的数量K,但在实际应用中这个值可能难以估计,选择不当会影响最终聚类效果。
- 对初始质心敏感:算法收敛结果依赖于初始质心的选择,不同的初始质心可能导致不同的聚类结果。
- 陷入局部最优:由于采用迭代优化方法,容易陷入局部最优,无法保证找到全局最优解。
- 对异常值敏感:算法基于欧氏距离度量,因此对噪声点和离群点非常敏感,这些点可能严重影响聚类中心的位置。
四、预设K值等于几?
我怎么知道要聚成几类呢?K-means算法的关键在于K值的选择,即最终要形成的簇的数量。K值的选择对聚类结果有很大影响,通常使用肘部法则(Elbow Method)或轮廓系数 (Silhouette Coefficient)等技术来选择最佳的K值。
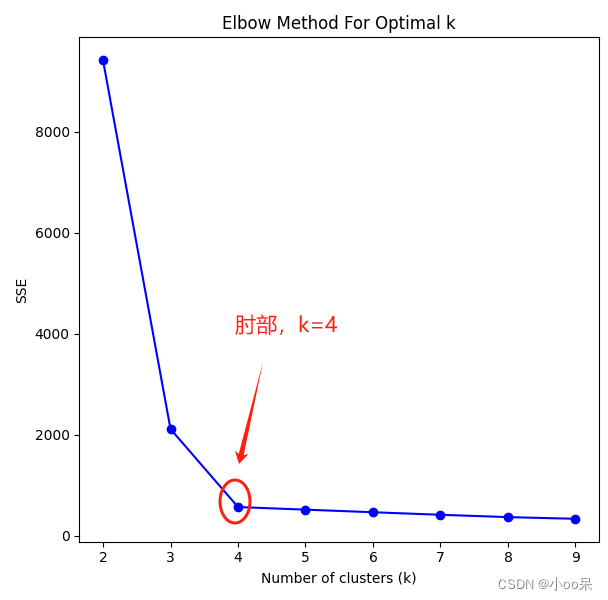
(1)肘部方法
运行K-means算法多次,每次使用不同的K值,通过绘制不同K值下代价函数值(即各个样本点到其所属簇中心的平方误差之和,简称SSE=Sum of Squared Errors)与K的关系图,寻找曲线“弯折”的位置,即增加K值时SSE下降速度明显减缓的那个点作为最佳K值。
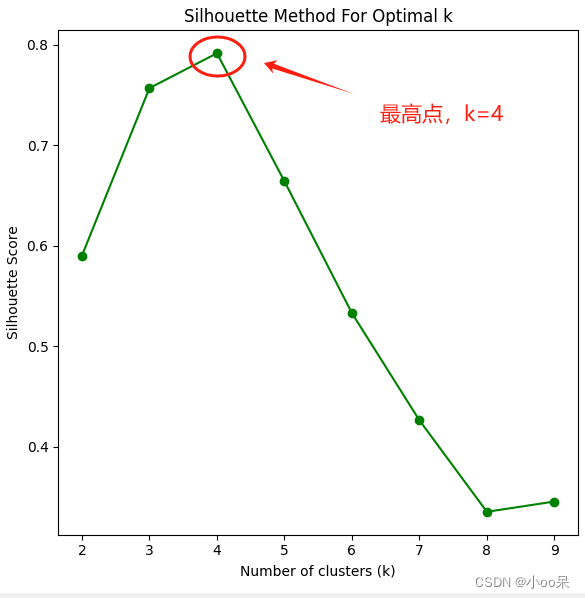
(2)轮廓系数
计算每个样本点的轮廓系数,该系数衡量了样本点与其所在簇内其他样本的相似度与它与其他簇样本点的差异程度。当所有样本点的平均轮廓系数达到最大时对应的K值是较好的选择。