在明确如何度量参与方组合数据价值的基础上, 本篇介绍如何进一步度量参与方在联邦合作中的贡献, 具体介绍如下 4 种参与方贡献评估方案.

• 个体法
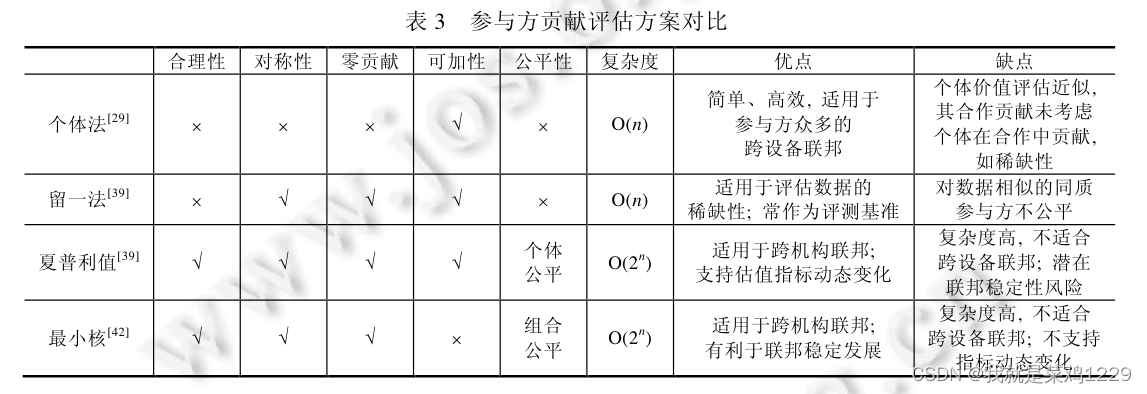
  • 将参与方自身数据的价值度量或者相关变体作为该参与方的贡献. 个体法可以基于任何 数据价值度量指标进行, 特别地, 有个体信誉、个体交叉验证、个体互信息、个体采样和 个体影响函数等指标. 个体法简单、高效, 未考虑参与方个体为联邦集体的价值增益, 适用于参与 方数量众多的跨设备联邦场景.
• 留一法
  • 将联邦全体中移除某个参与方造成的数据价值损失作为该参与方的贡献. 留一法仅考虑 了全体组合下某个参与方带来的价值增益, 对于多个相似互可替代的参与方不公平, 适合于发掘稀 缺性参与方的场景, 常被作为其他方案评测的基准方法.
• 夏普利值
  • 枚举所有可能的参与方组合, 将参与方加入联邦的数据价值边际增益期望作为其贡献. 夏普利值方案直观、便于理解, 保证了对每个参与方个体贡献评估的公平性, 在目前联邦贡献评估中 应用最为广泛.
• 最小核
  • 将各参与方贡献估计转化为最优化问题, 其优化目标为任意参与方组合的贡献之和尽可 能地大于其组合数据价值. 最小核方案设计上最优化子组合贡献分配, 保证了参与方子组合贡献评 估相对于组合价值的公平性, 更加符合经济规律, 所以有利于联邦的长期稳定发展.

1.个体法

顾名思义, 个体法(individual)直接基于参与方自身的数据价值度量或者相关变体来评估参与方在联邦中 的贡献:
ϕ i = v ( { i } ) \phi_i = v(\{i\}) ϕi​=v({i})
其中${\varphi }_i$代表参与方i在联邦中的贡献， v ( { i } ) v(\{i\}) v({i})代表在价值度量指标 v 下参与方 i 的数据价值。个体法的价值度 量除了直接采用第 2 节介绍的价值度量指标之外, 还研究开发了如下基于个体信誉、交叉验证、互信息、采 样实验和影响函数的专用方法.

1.1 个体信誉法

在假定有参与方数据价值评分的信誉系统中, 个体信誉法通过参与方历史参与联邦学习的信誉来评估参 与方对联邦合作的贡献。
参与方信誉可分为直接信誉和间接信誉。
直接信誉包含对参与方训练的局部模型 质量测评和参与方的活跃度: 对于局部模型的质量评测可反映参与方数据的可靠性; 参与方的活跃度可以评 估参与方信誉的实时有效性, 信誉值随参与活跃度降低而衰减
间接信誉表示参与方在历史联邦学习任务中 的信誉情况, 即同时考虑多个任务之间参与方信誉反馈的一致性来避免恶意欺诈.
参与方个体信誉法采用多权重的主观逻辑模型来加权融合多个信誉评估, 综合评估参与方对联邦合作的贡献.

1.2 个体交叉验证法

对于需要估计参与方数据标签质量以及与联邦测试集一致性的场景中, 通过参与方本地模型和本地测试 集与联邦全局模型和联邦测试集进行交叉测试实验来评估参与方对联邦合作的贡献。

具体而言, 该方法同时考 虑参与方本地数据训练的模型在联邦测试集上的交叉熵, 以及联邦全局模型在参与方本地数据上的交叉熵. 交叉验证的交叉熵之和越小, 参与方数据标签噪声及与联邦测试集分布差异性越小, 参与方标签质量越高, 对联邦合作的贡献越大.

缺点：为此, 在全体参与方合作训练联邦模型的同时, 各参与方需要基于本地数据额外训 练一个本地模型以计算对联邦测试集的交叉熵.

1.3 个体互信息法

针对希望识别低价值或者恶意参与方的场景, 个体互信息法通过参与方个体之间的互信息来评估参与方对联邦合作的贡献。

该方法无须训练联邦模型, 每个参与方基于本地数据训练局部模型, 某个参与方对 联邦的贡献是多个其他随机采样参与方的局部模型与该参与方局部模型的互信息量平均值 , 互信息量越高, 则该参与方与其他参与方之间数据关联性越强, 说明该参与方提供的数据越可信.

实践中, 为了评估参与方 局部模型之间的互信息, 该方法需通过模型参数压缩技术将模型参数离散化, 并基于模型间的相关性预测 技术量化参与方模型间的互信息。

1.4 个体采样实验法

基于联邦学习全体参与方共同训练全局模型的设定, 可以设法直接在训练全局模型的同时, 完成各参与 方的贡献评估, 以减少每个参与方额外训练模型的代价.
联邦学习训练过程中, 每轮次各参与方的数据会全 部参与训练计算梯度, 如果随机改变各参与方数据的参与比例, 则相应的训练后联邦模型测试准确率会发生 变化. 基于这样的观察, 可以调节不同的参与方数据参与比例, 重复训练多个联邦模型, 从而获得多个对应的 测试准确率结果, 并基于深度学习技术来拟合各参与方采样率与联邦测试准确率的关系。

由于联邦模型训 练有多个轮次, 对于每个轮次可以重新随机采样不同比例的参与方数据量, 并获得对应轮次的测试准确率, 再通过采用序列化深度模型的方式, 拟合多轮次的测试结果来评估参与方的贡献.

基于上述拟合随机采样比例与参与方贡献之间关系的启发, 可进一步引入强化学习算法, 通过交互式的反馈, 动态地调节参与方采样比例 , 使得联邦模型测试准确率快速地收敛到最高, 并将最优情况下的参与方 数据被采样比例作为该参与方对联邦合作的贡献。

如果某个参与方参与比例越大时联邦模型准确率越高, 则该参与方的数据贡献越大. 在此强化学习模型的定义中, 强化学习模型的状态空间是每轮次全局模型的更新梯度, 决策空间是参与方数据被采样比例或局部梯度被采样比例, 奖励函数是强化学习决策带来的联邦测 试准确率的变化. 类似地, 在没有测试集的条件下, 也可以通过强化学习的方式, 调整不同参与方的数据参与 比例, 使得联邦模型的训练损失最小化, 并将最终强化学习模型收敛时各参与方最优参与比例作为参与方对 联邦的贡献。

1.5 个体影响函数法

上述参与方采样比例评估法在评估参与方个体在联邦学习中的贡献时, 仍需要重复多次训练联邦模型, 以验证何种参与比例下联邦模型最优.
如果只希望训练单个联邦模型, 不再额外训练局部模型, 则可以采用 影响函数技术进行参与方贡献评估。
影响函数(influence function)[49]是鲁棒统计中的经典技术. 它被用来评 估对训练样本的微小扰动给模型参数带来的影响, 比如量化追踪移除或者微小改变部分训练数据后对机器学 习模型测试准确率带来的影响.

2 留一法

留一法(leave one out)在机器学习任务中被广泛应用于交叉验证[51]. 基于留一法的思想, 可以将联邦排除 掉某个参与方后的参与方组合价值边际损失作为该参与方对联邦的贡献。

缺点：留一法只考虑了其他参与方全部保留下某个参与方为联邦 所带来的边际收益, 这种指定参与方最后加入联邦来评估贡献的方式同样存在公平性问题. 比如, 当存在多 个参与方持有相同但对联邦高价值的数据时, 移除掉持有该数据的参与方中任何一个均不会对联邦测试准确 率带来显著影响, 这些参与方会被评估为低价值, 但同时, 移除这些参与方将大大降低联邦的性能。

3 夏普利值

1953 年, 夏普利值(shapley value)被提出来以解决合作博弈问题。后来, 夏普利博弈(shapley game)被广 泛用来评估联邦学习中的参与方贡献, 该方案将每个参与方的夏普利值视为该参与方的贡献。
----在之后的文章中详细讲解一下

4 核方法

根据核理论, 联邦对参与方的贡献(回报)评估中, 任何子组 合的贡献和应大于等于该组合的数据价值. 当目标无法实现时, 需要将潜在子组合中的最大亏损值最小化, 即最小核方法(least core). Yan 等人分析了夏普利值法优化个体公平性的局限性, 认为最小核方案保证了任何 子组合获得相对于组合价值贡献应得的贡献评估, 是从追求联邦长久稳定性的角度上参与方贡献评估的可行方案。
----在之后的文章中详细讲解一下

总结

个体法和留一法对参与方贡献的度量简单、高效, 贡 献评估代价随着参与方数量线性增长. 但是这两种方法不满足贡献评估的公平合理性需求, 无法公平、有效 地度量各参与方在联邦合作中的贡献. 比如, 它们无法兼顾考虑到不同参与方持有相似数据集或互补数据集 下的评估合理性, 无法为联邦发掘出最优的参与方组合, 获取对联邦最完备有效的任务数据.

夏普利值和最 小核方法均满足合理性、对称性和零贡献性质, 满足联邦合作贡献评估的公平合理性需求, 但这相应地使得 贡献评估需枚举全部 $2^n$种参与方组合, 评估时间代价随参与方数量呈指数增长. 从贡献评估方案与价值度量 指标相关性出发, 个体法方案与价值度量指标选择依赖性强, 衍生出了基于个体信誉、影响等专用指标; 留一 法、夏普利值和最小核方案与价值度量指标选择正交, 即可实现方案与价值度量指标的任意组合.

从联邦分类出发, 本节所有方案均适用于横向和纵向联邦, 由于简单、高效(线性复杂度)的优势, 个体法和留一法更适 合于参与方数量众多的跨设备联邦; 同时满足公平合理性的夏普利值和最小核方案由于复杂度高, 更适合于 参与方数量较少的跨机构联邦.

对比夏普利值和核最小核方法来看, 主要区别是夏普利值满足可加性而不满足稳定性, 最小核不满足可 加性但满足稳定性. 可加性使得夏普利值在评估后线性地新增价值度量指标时, 不再需要额外对已完成评估 的价值度量指标进行重复评估, 可以大大减少重复评估代价. 当评估任务能够一次性了解全部价值度量指标 时, 可以将多个价值度量指标复合成单个价值函数, 这时, 对评估方案的可加性要求是不必要的. 另一方面, 夏普利值考虑了所有加入联邦次序下参与方的边际价值增益, 满足了个体层面的公平性; 最小核保证任何参 与方子组合获得相对于组合数据价值应得的贡献评估并给予相应回报激励, 满足了任意参与方组合下的公平 性, 即联邦稳定性. 如果从经济角度联邦(或者数据集市)的长远发展出发, 最小核方法的稳定性特性有助于联邦的长期稳定发展需要, 避免了某些参与方子组合为追求更大收益结对离开联邦的问题.

有趣的点

个体采样实验法：联邦学习+强化学习用来对于参与方的贡献进行评估。
最小核方案在联邦学习上的应用