C语言数据结构易错知识点（3）（堆）

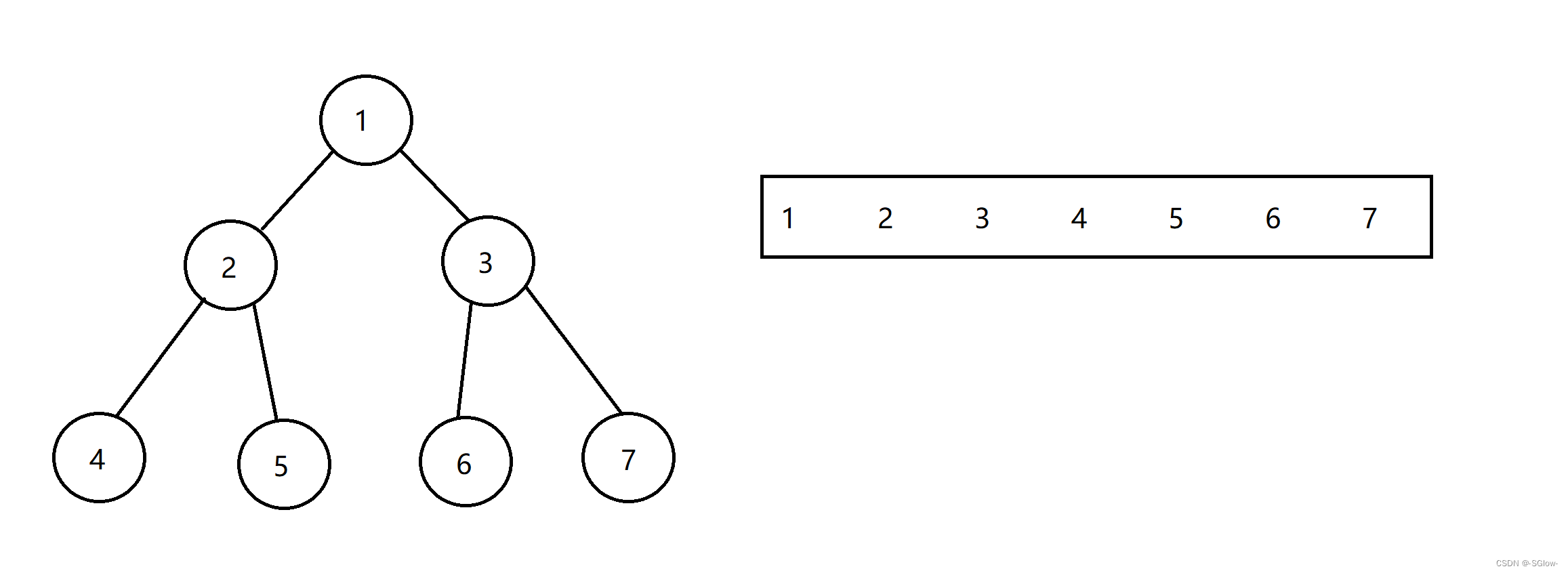
1.堆的本质：完全二叉树

堆在物理结构上是顺序结构，实现方式类似于顺序表（数组）；但在逻辑结构上是树形结构，准确来说堆是一棵完全二叉树。因为堆的实现在代码上和顺序表有很高的相似度，所以在写代码时，我们要仔细理解堆的逻辑结构，理解每步操作对该二叉树的影响，我们也可以画画简图，更加直观地感受堆的相关操作的含义。

2.向上调整与向下调整使用场景

当数据插入堆或从堆顶移除后，都要对堆进行相关的调整，使其成为一个新堆。调整方式分为向上调整和向下调整，它们有不同应用场景：

①向上调整：尾部插入数据时使用。当在尾部加入一个新的数据时，这个数据可能要和父节点交换后才能形成大（小）堆，交换过程中除了新插入的节点可能不满足堆的规则以外，其余节点都不需要调整。

函数参数参考：void AdjustUp(HPDataType* arr, int child);

下面举个例子：

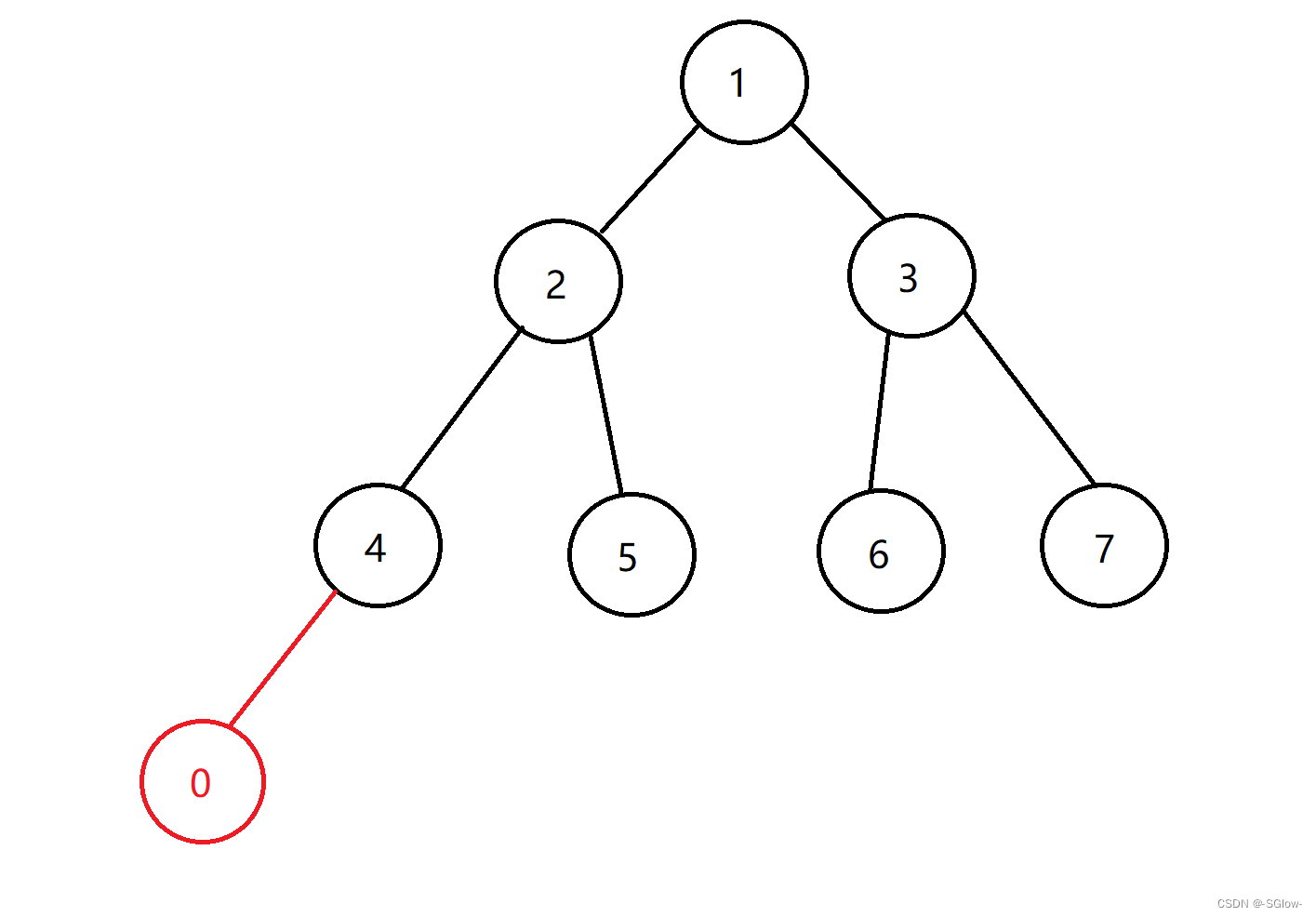
对于这个小堆，这里新插入了一个0，需要进行调整，我们这时选择向上调整，即沿着祖先向上调整，其余部分不调整

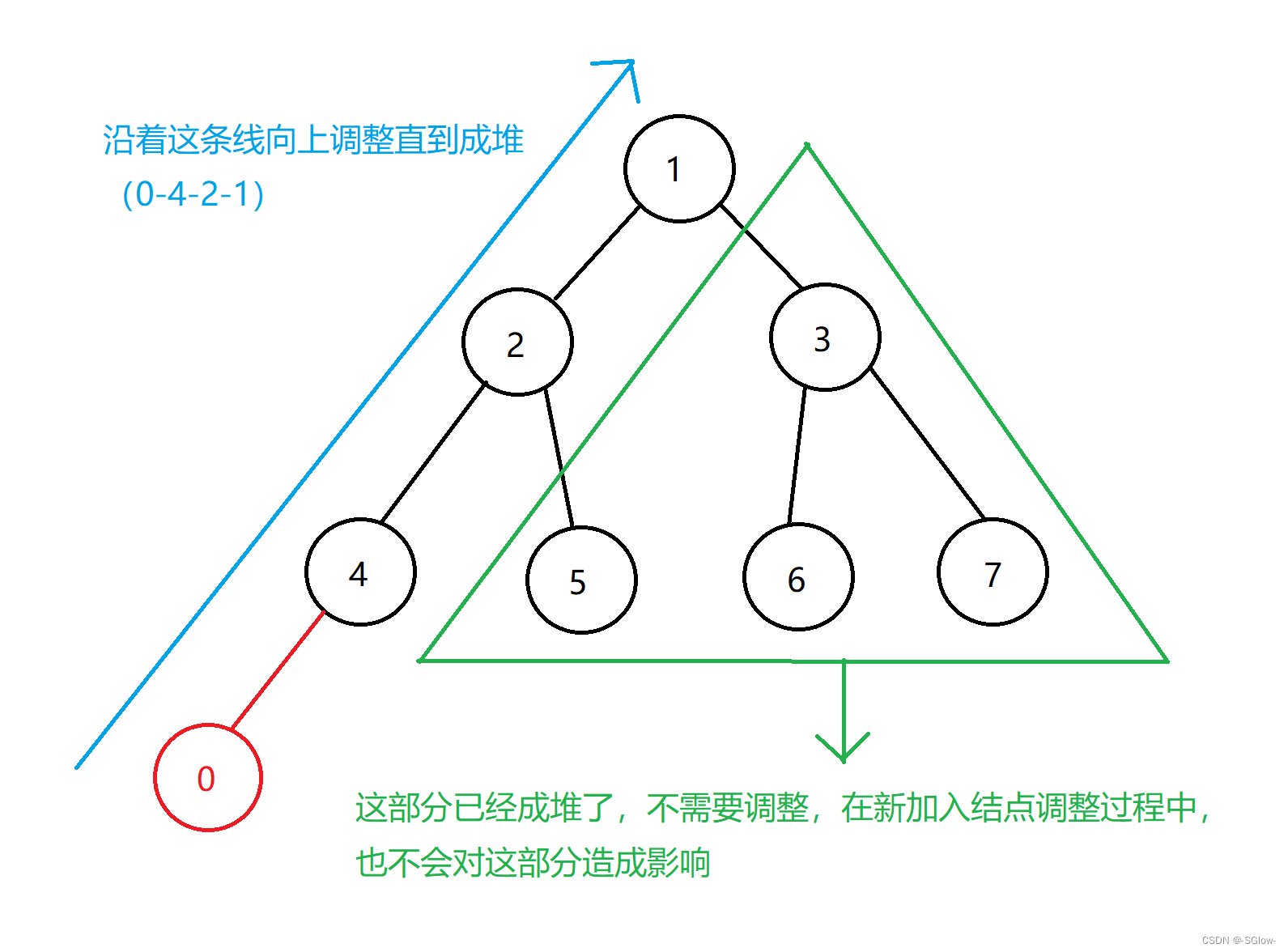
②向下调整：当数据从堆顶移除或建堆时使用。

函数参数参考：void AdjustDown(HPDataType* arr, int size, int parent);

a.从堆顶移除数据时向下调整：先交换首元素和尾元素，并用顺序表的方式让size--，使得最后一个元素被删除，再向下调整直到成堆

b.建堆：建堆一般来说有两种方式，一种是向上调整，每次新插入一个元素后向上调整直到成堆；另一种是向下调整，在加入所有数据后从倒数第二行开始向下调整直到成堆。一般来说，我们采用向下调整，因为对于建堆而言，向下调整的时间复杂度近似为O(N-logN)或O(N)，而向上调整的时间复杂度为O(NlogN)，下面简单讲解一下：

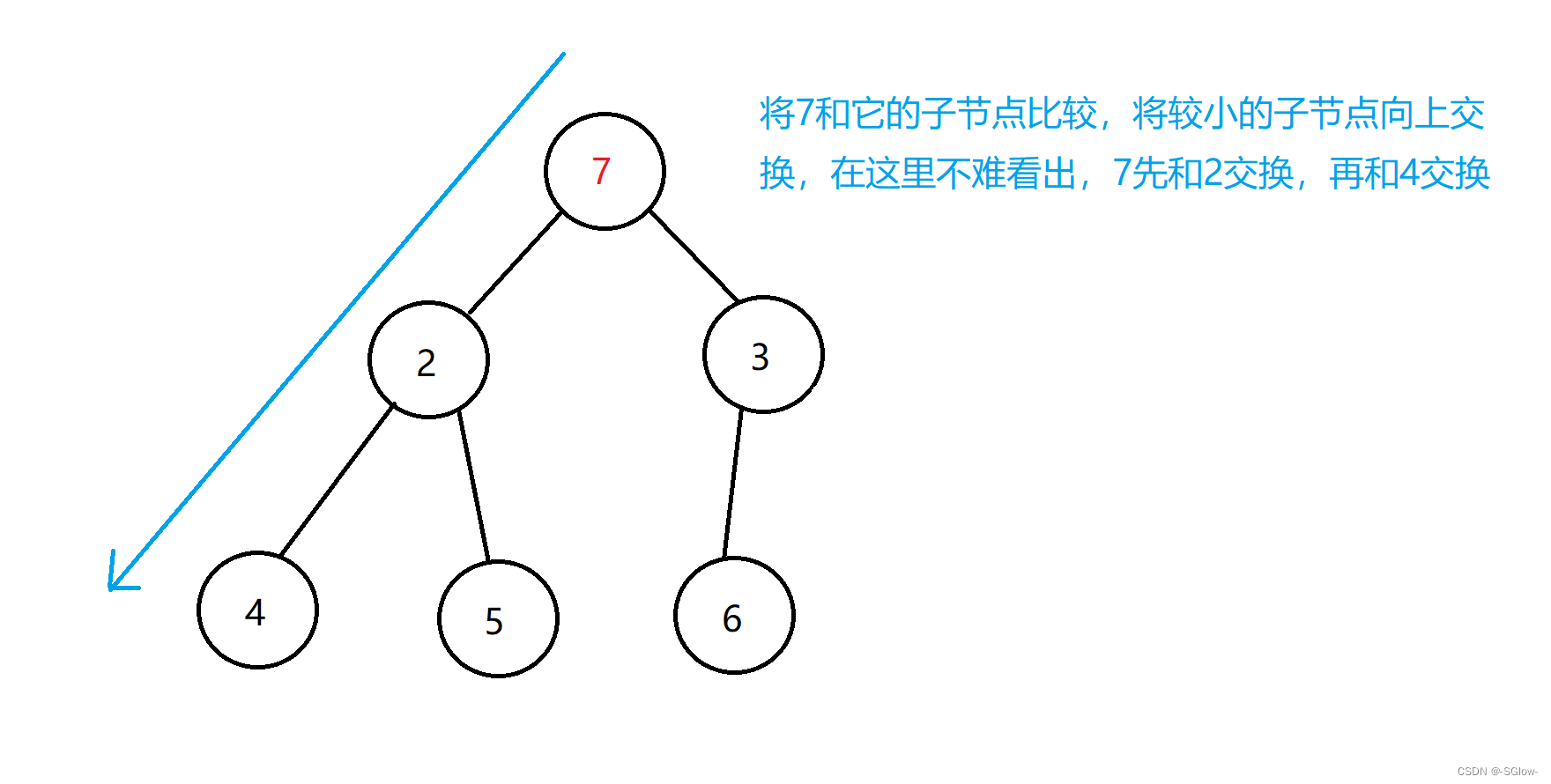
向上调整建堆：共有N个元素，每次向上调整logN次，时间复杂度O(logN)

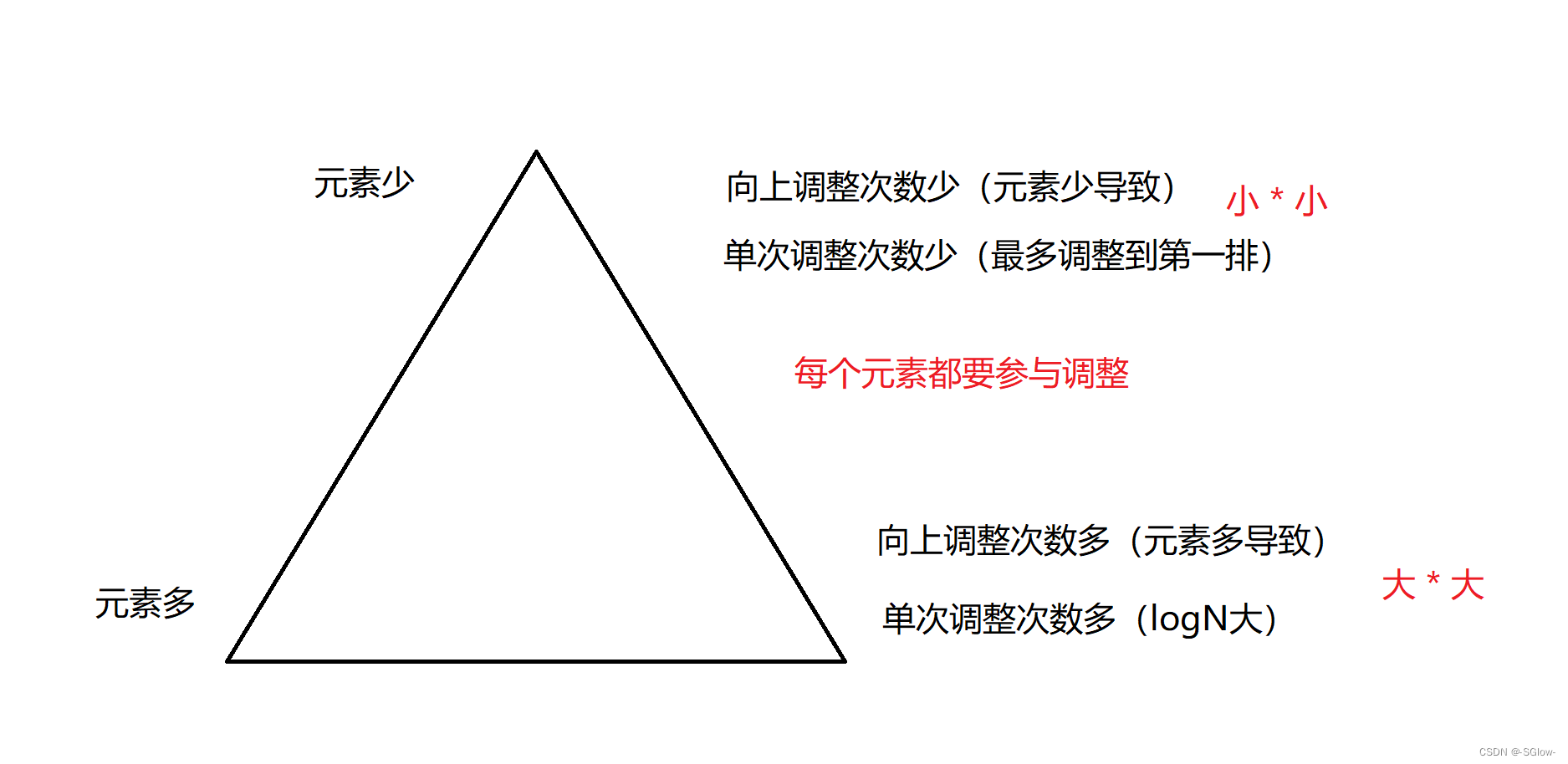
向下调整建堆：第一眼看上去虽然也是O(NlogN)，但多观察就发现调整次数远远小于向上调整

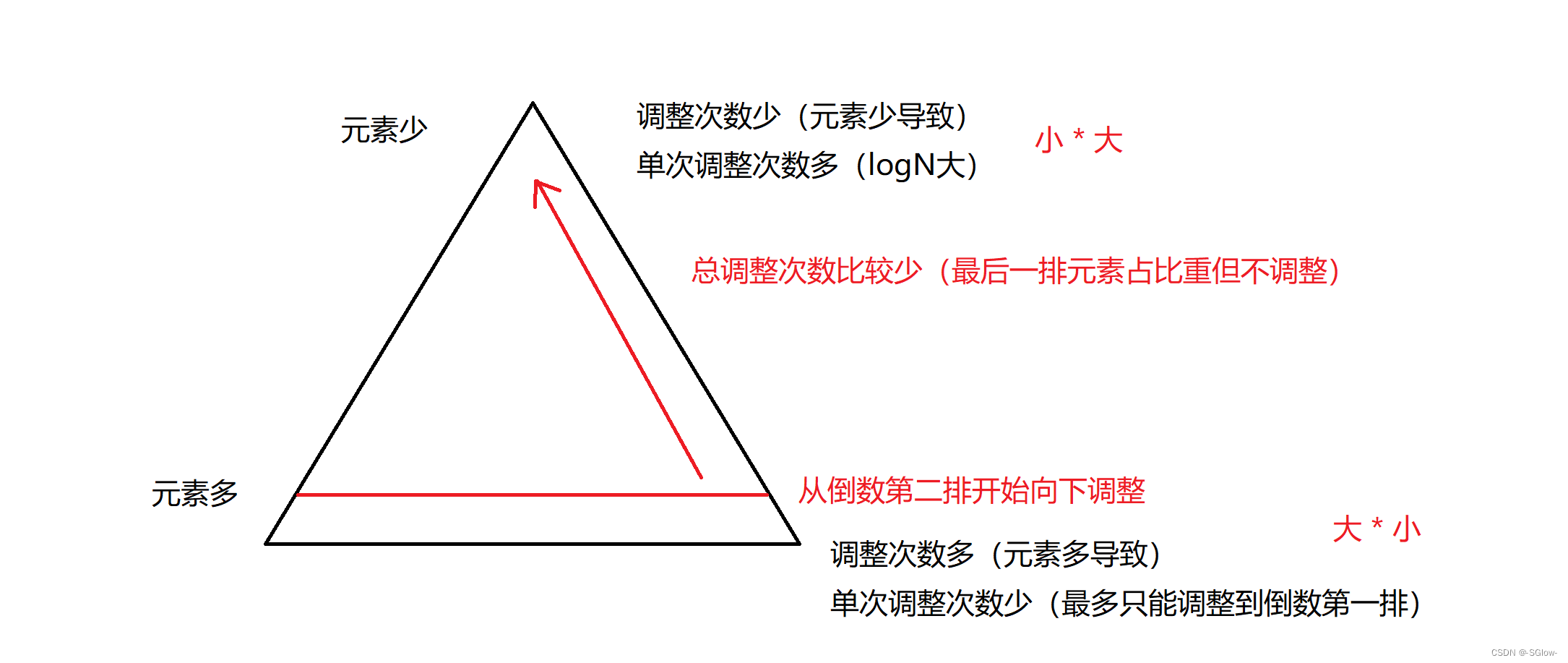
经过详细计算可知比较准确的时间复杂度是O(N-logN)，可以再近似于O(N)，但我们不用特别纠结于如何精确计算时间复杂度，而是要像上面两张图那样学会粗略地分析和计算

3.堆排序：如果一来就学习堆排序的话，其实会很困难，但如果学会了堆的相关操作，掌握向上和向下调整之后，堆排序就非常简单了。

我们需要用到的知识点就只有：(子节点-1) / 2 == 父节点，父节点 * 2 + 1 == 左孩子结点，父节点 * 2 + 2 == 右孩子结点，堆删除的思路，向下调整。

堆删除的思路对堆排序来说很重要，关键在于首元素和尾元素的交换。

堆排序关键思路：当我们想让数组从小到大排序，则建立大堆；从大到小排序，则建立小堆。当我们通过大堆找到最大值后，将其与尾元素交换，然后size--达到伪删除的目的（顺序表的删除也可视为一种伪删除，即数据没有被销毁，只是访问不到），重复建堆并交换，次大的数据在最大的数据之前，以此类推......

堆排序的实现注意事项：我们实现堆排序的时候，不要像实现堆那样开辟一整块空间，再push数据、建堆等操作。我们直接在数组上建堆，因为堆排序的物理结构归根到底还是顺序表，只要熟悉堆的操作，我们直接通过下标进行访问修改即可。

Topk问题：这类问题的关键就是要建立k个元素的堆，从小到大排序，则建立大堆；从大到小排序，则建立小堆，从第k + 1个数开始每次删去堆顶元素，再push一个数至堆顶，再向下调整。满足条件的数沉入堆底，不会被删除。理解了这里，那么Topk问题就迎刃而解了。

4.堆和堆排序实现代码：

Heap.h

#pragma once#include <stdio.h>#include <stdlib.h>#include <assert.h>#include <stdbool.h>typedef int HPDataType;typedef struct Heap
{HPDataType* arr;int size;int capacity;}Heap;void HeapInit(Heap* p);void HeapDesTroy(Heap* p);void HPDataTypeSwap(HPDataType* x1, HPDataType* x2);void AdjustUp(HPDataType* arr, int child);void AdjustDown(HPDataType* arr, int size, int parent);void HeapPush(Heap* p, HPDataType x);void HeapPop(Heap* p);bool HeapEmpty(Heap* p);int HeapSize(Heap* p);HPDataType HeapTop(Heap* p);void HeapSort(HPDataType* arr, int size);

Heap.c

#pragma once#include "Heap.h"void HeapInit(Heap* p)
{assert(p);p->capacity = p->size = 0;p->arr = NULL;
}void HeapDesTroy(Heap* p)
{assert(p);free(p->arr);p->arr = NULL;p->capacity = p->size = 0;
}void HPDataTypeSwap(HPDataType* x1, HPDataType* x2)
{assert(x1 && x2);HPDataType tmp = *x1;*x1 = *x2;*x2 = tmp;
}void AdjustUp(HPDataType* arr, int child)
{assert(arr);int parent = (child - 1) / 2;while (child > 0){if (arr[child] < arr[parent]){HPDataTypeSwap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void AdjustDown(HPDataType* arr, int size, int parent)
{assert(arr);int child = parent * 2 + 1;if (parent * 2 + 2 < size){child = arr[child] < arr[child + 1] ? child : child + 1;}while (child < size){if (arr[child] < arr[parent]){HPDataTypeSwap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;if (parent * 2 + 2 < size){child = arr[child] < arr[child + 1] ? child : child + 1;}}else{break;}}}void HeapPush(Heap* p, HPDataType x)
{assert(p);if (p->capacity == p->size){p->capacity = p->capacity == 0 ? 4 : 2 * p->capacity;HPDataType* tmp = (HPDataType*)realloc(p->arr, sizeof(HPDataType) * p->capacity);assert(tmp);p->arr = tmp;}p->arr[p->size++] = x;AdjustUp(p->arr, p->size - 1);
}void HeapPop(Heap* p)
{assert(p);HPDataTypeSwap(&p->arr[0], &p->arr[p->size - 1]);p->size--;AdjustDown(p->arr, p->size, 0);
}bool HeapEmpty(Heap* p)
{assert(p);return p->size == 0;
}int HeapSize(Heap* p)
{assert(p);return p->size;
}HPDataType HeapTop(Heap* p)
{assert(p);if (p->size == 0){printf("空堆，无数据\n");assert(p->size != 0);}return p->arr[0];
}void HeapSort(HPDataType* arr, int size)
{assert(arr);int parent = (size - 2) / 2;while (parent >= 0){AdjustDown(arr, size, parent);parent--;}int sz = size;while (--size){HPDataTypeSwap(&arr[0], &arr[size]);AdjustDown(arr, size, 0);}for (int i = 0; i < sz; i++){printf("%d ", arr[i]);}}

堆测试代码：


#include "Heap.h"//小堆的相关功能实现int main()
{Heap p;HeapInit(&p);HPDataType arr[] = { 10, 9, 8, 7, 4, 5, 6, 2, 1, 3, 12, 11, 13, 15, 14, 16, 19, 17, 18, 20 };for (int i = 0; i < sizeof(arr) / sizeof(HPDataType); i++){HeapPush(&p, arr[i]);}while (HeapEmpty(&p) != true){printf("%d ", HeapTop(&p));HeapPop(&p);}HeapDesTroy(&p);return 0;
}

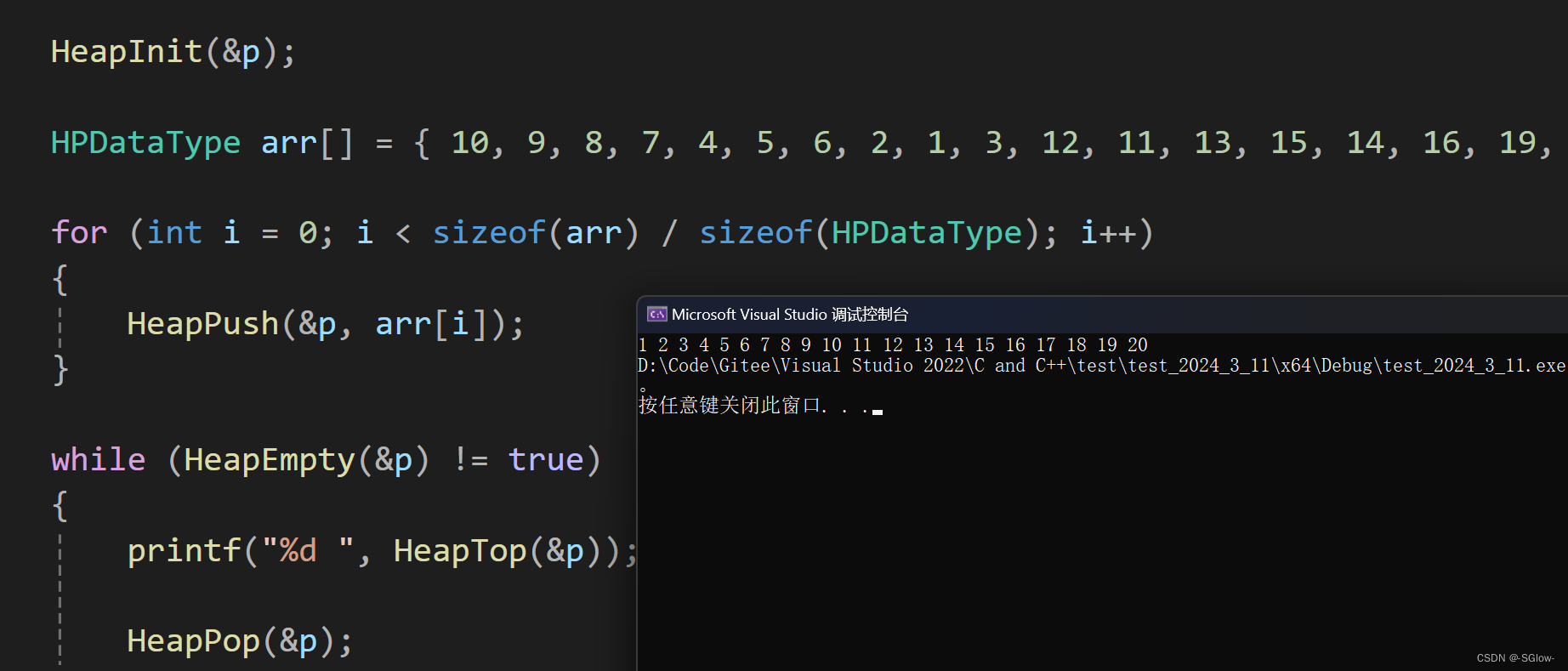
堆排序测试代码：


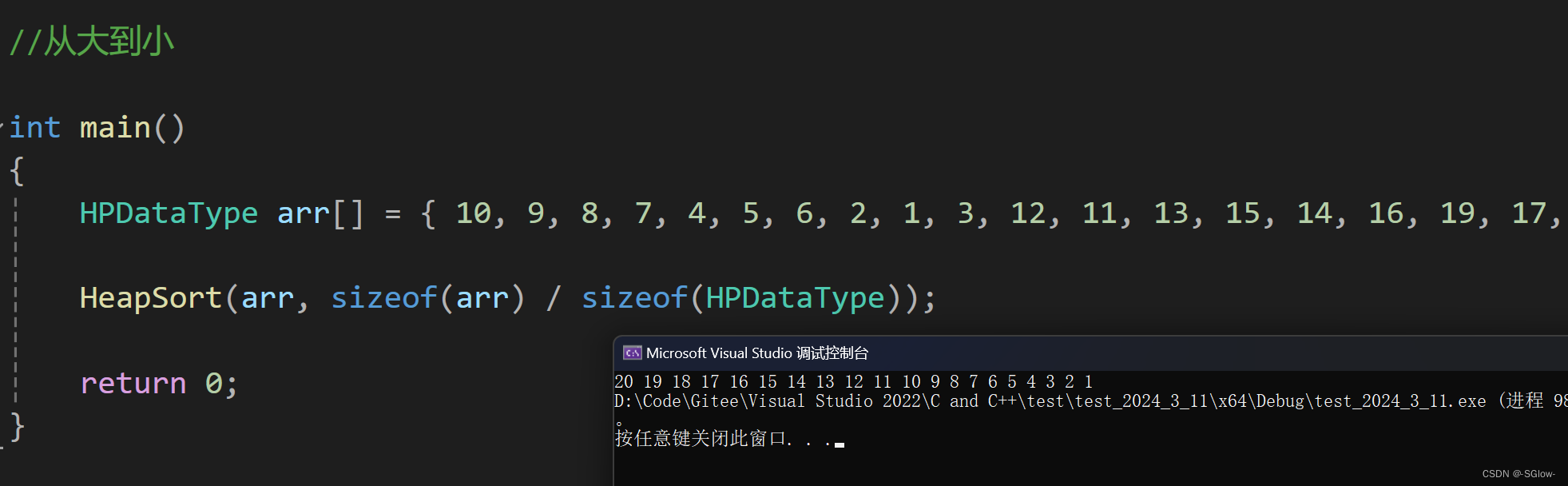
#include "Heap.h"//从大到小int main()
{HPDataType arr[] = { 10, 9, 8, 7, 4, 5, 6, 2, 1, 3, 12, 11, 13, 15, 14, 16, 19, 17, 18, 20 };HeapSort(arr, sizeof(arr) / sizeof(HPDataType));return 0;
}