所谓递推，是指从已知的初始条件出发，依据某种递推关系，逐次推出所要求的各中间结果及最后结果。其中初始条件或是问题本身已经给定，或是通过对问题的分析与化简后确定。
从已知条件出发逐步推到问题结果，此种方法叫顺推。
从问题出发逐步推到已知条件，此种方法叫逆推。
无论顺推还是逆推，其关键是要找到递推式。这种处理问题的方法能使复杂运算化为若干步重复的简单运算，充分发挥出计算机擅长于重复处理的特点。

算法特点：

• 1.问题可以划分成多个状态；
  2.除初始状态外，其它各个状态都可以用固定的递推关系式来表示。
  在我们实际解题中，题目不会直接给出递推关系式，而是需要通过分析各种状态，找出递推关系式。

例题1：树塔问题

描述：

树塔问题，编写程序计算从顶到底的某处的一条路径，使该路径所途径的数字最大

#include<bits/stdc++.h>
using namespace std;
int main() {int n, a[101][101];cin >> n;int sum =0;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {cin >> a[i][j];}
}for (int i = n; i >= 1; i--) {int max = a[i][1];for (int j = 1; j <= i; j++) {if (a[i][j] > max) {max = a[i][j];}}sum += max;}cout << sum << endl;return 0;
}

---

例题2：斐波那契数列第N项

#include<bits/stdc++.h>
using namespace std;
int main() {int f0 = 1, f1 = 1, f2,n;cin >> n;for (int i = 3; i <= n; i++) {af2 = f1 + f0;f0 = f1;f1 = f2;}cout << f2;return 0;
}

---

例题3：昆虫繁殖

描述

科学家在热带森林中发现了一种特殊的昆虫，这种昆虫的繁殖能力很强。每对成虫过x个月产y对卵，每对卵要过两个月长成成虫。假设每个成虫不死，第一个月只有一对成虫，且卵长成成虫后的第一个月不产卵(过x个月产卵)，问过z个月以后，共有成虫多少对？0≤x≤20,1≤y≤20,X≤z≤50

#include <iostream>
using namespace std;
#include <cstdio>
int a[25], b[25];
void fun(int x,int y,int z)
{a[1] = 1; b[1] = 0;for (int i = 1; i <= x; i++){a[i] = 1;b[i] = 0;}for (int i = x + 1; i <= z+1; i++)　{：a[i] = a[i - 1] + b[i - 2];b[i] = a[i - x] * y;   　}cout << a[z+1];
}
int main()
{int x, y, z;cin >> x >> y >> z;fun(x,y,z);
}

---

例题4：位数问题

描述

在所有的 N 位数中，有多少个数中有偶数个数字 3？由于结果可能很大，你只需要输出这个答案对 12345 取余的值。

#include<bits/stdc++.h>
using namespace std;
bool is_even(int a) {int count = 0;while (a != 0) {int ge = a % 10;if (ge == 3) { count++; }a /= 10;}if (count % 2 == 0) {return true;}else {return false;}
}
int main() {int n;cin >> n;int count = 0;for (int i = pow(10,n-1); i <= pow(10, n) - 1; i++) {if (is_even(i)) {count++;}}cout << count % 12345 << endl;return 0;
}

---

五种递推问题：

·Fibonacci数列

·Hanoi塔问题

·平面分割问题

·Catalan数

·第二类Stirling数

---

习题：

1.上台阶

楼梯有n(71>n>0)阶台阶,上楼时可以一步上1阶,也可以一步上2阶,也可以一步上3阶，编程计算共有多少种不同的走法。

#include<cstdio>  
long long d[100]= {0};  
int main()
{  d[1]=1;d[2]=2;d[3]=4;  for(int i=4; i<=100; i++)d[i]=d[i-1]+d[i-2]+d[i-3];  int a;  while(scanf("%d",&a)==1&&a)   printf("%lld\n",d[a]);  return 0;  
}  

---

2.流感传染

有一批易感人群住在网格状的宿舍区内，宿舍区为n*n的矩阵，每个格点为一个房间，房间里可能住人，也可能空着。在第一天，有些房间里的人得了流感，以后每天，得流感的人会使其邻居传染上流感，（已经得病的不变），空房间不会传染。请输出第m天得流感的人数。

第一行一个数字n，n不超过100，表示有n*n的宿舍房间。

接下来的n行，每行n个字符，’.’表示第一天该房间住着健康的人，’#’表示该房间空着，’@’表示第一天该房间住着得流感的人。

接下来的一行是一个整数m，m不超过100。

#include<bits/stdc++.h>
using namespace std;
char a[101][101]
int main() {int n,day,count=0;cin >> n;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {cin >> a[i][j];}}cin >> day;for (int i = 2; i <= day; i++) {for (int j = 1; j <= n; j++) {for (int k = 1; k <= n; k++) {if (a[j][k] == '@') {if (a[j][k + 1] == '.') {a[j][k + 1] = '!';}if (a[j][k -1] == '.') {a[j][k -1] = '!';}if (a[j+1][k] == '.') {a[j+1][k] = '!';}if (a[j-1][k] == '.') {a[j-1][k] = '!';}}}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (a[i][j] == '!') {a[i][j] = '@';}}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {cout << a[i][j] << " ";}cout << endl;}cout << endl;}for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (a[i][j] == '@') {count++;}}}cout << endl;cout << count;return 0;
}

---

*3.山区建小学

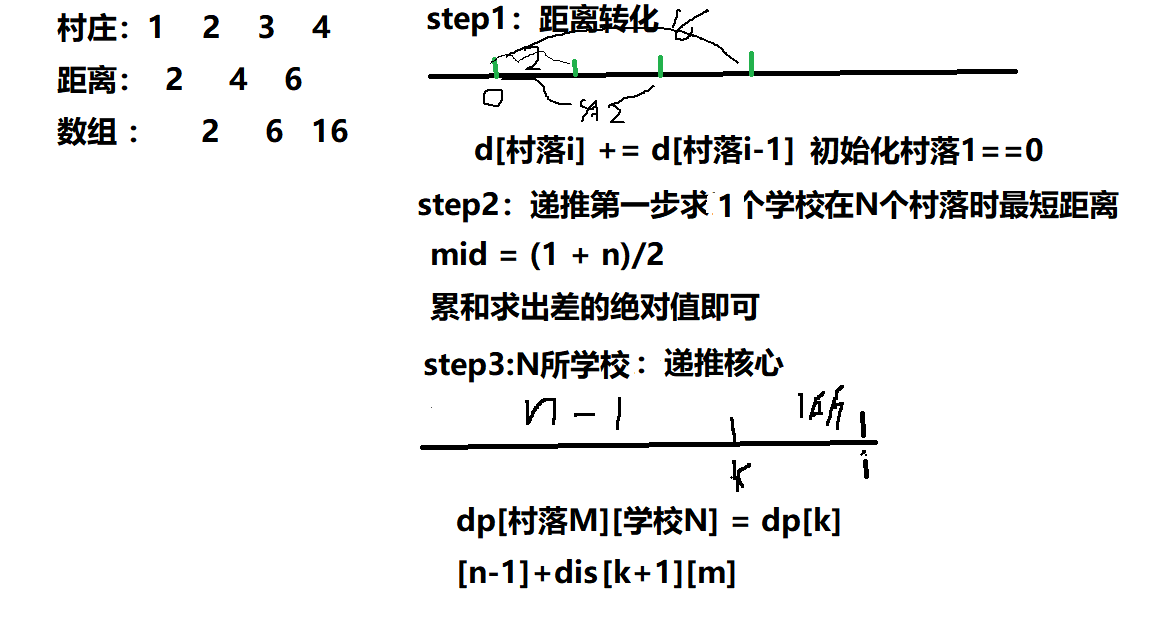
政府在某山区修建了一条道路，恰好穿越总共m个村庄的每个村庄一次，没有回路或交叉，任意两个村庄只能通过这条路来往。已知任意两个相邻的村庄之间的距离为di(为正整数)，其中，0<i<m。为了提高山区的文化素质，政府又决定从m个村中选择n个村建小学(设0<n≤m<500)。请根据给定的m、n以及所有相邻村庄的距离，选择在哪些村庄建小学，才使得所有村到最近小学的距离总和最小，计算最小值。

第1行为m和n，其间用空格间隔

第2行为m−1个整数，依次表示从一端到另一端的相邻村庄的距离，整数之间以空格间隔。

#include<bits/stdc++.h>
using namespace std;
int dis[100][100], dp[100][100], d[100];
//dis两村庄中建立一所学校的最小距离
//d村庄到原点的距离
//dp最小距离
int cal(int x, int y) {int mid = (x + y) / 2,ans = 0;for (int i = x; i <= y; i++) {ans += abs(d[i] - d[mid]);}return ans;
}
int min(int x, int y) {return x > y ? y : x;
}
int main() {int m, n;cin >> m >> n;for (int i = 2; i <= m; i++) {cin >> d[i];d[i] += d[i - 1];}//建立一所学校for (int i = 1; i <= m; i++) {for (int j = i; j <= m; j++) {dis[i][j] = cal(i, j);}}//建立n所学校for (int i = 1; i <= m; i++) {for (int j = 1; j <= n && j<=i; j++) {dp[i][j] = 999999;for(int k =1;k<i;k++){if (j == 1) { dp[i][j] = dis[1][i]; }else{dp[i][j] = min(dp[i][j], dp[k][j-1] + dis[k+1][i]);}}}}cout << dp[m][n];return 0;
}