刷题笔记(2)

二分查找

在排序数组中查找元素的第一个和最后一个位置

[传送门]( 34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode） )

class Solution {
public://求出第一个大于等于target的下标int ans(vector<int>& nums, int target){int left = 0, right = nums.size() - 1, mid;//左闭右闭区间while(left <= right){mid = left + (right-left)/2;//先减后加防止溢出if(nums[mid] < target){left = mid + 1;}else{right = mid - 1;}}return left;}vector<int> searchRange(vector<int>& nums, int target) {int start = ans(nums, target);if(start == nums.size() || nums[start] != target){return {-1, -1};}int end = ans(nums, target+1) - 1;return {start, end};}
};

看完灵神讲完这题也算是开眼界了，原来二分查找也不仅仅针对找到target值，其实也能找到>=target或<=target的值。题解的ans函数就是找到该数组第一个>=target的下标，然后就是要搞清return的值是哪个，这里return的是left，因为循环结束之后left是在right的右边一个位置，并且小于left下标所表示的值都是小于target的，那么最终left所指的值就是第一个>=target的下标。在ans函数中mid也是值得注意的：java和C++需要考虑到下标可能溢出的问题，就不能mid = (left+right)/2这样写，而应该mid = left + (right-left)/2这样写，一定是先减后加。

再就是主函数if条件是排出了特殊的情况：①数组中所有数都小于target②数组长度为0③数组中所有数都大于target。再就是求end，end表示最后一个>=target的下标，那么可以转化成第一个>=target+1左边的下标，这就是为什么ans函数后面要-1

寻找旋转排序数组中的最小值

[传送门]( 153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode） )

class Solution {
public:int findMin(vector<int>& nums) {int left = 0, right = nums.size()-2, mid;while(left <= right){mid = left + (right-left)/2;if(nums[mid] < nums[nums.size()-1]){right = mid -1;}else{left = mid + 1;}}return nums[left];}
};

从这一题能够看出，采用二分查找法的题目不一定是有序的，二分查找的模板大致都是相同的，难点主要在需要发现合适的判断条件。这里将数组最后一个元素设置为基准，因为它一定是蓝色的(符合条件的)，目标值一定在最后一个数或者是它之前的数，所以遍历的区间在[0,n-2]。

搜索旋转排序数组

[传送门]( 33. 搜索旋转排序数组 - 力扣（LeetCode） )

class Solution {
public:int search(vector<int>& nums, int target) {int left = 0, right = nums.size()-2, mid;while(left <= right){mid = left + (right-left)/2;if(nums[mid] < nums[nums.size()-1]) right = mid-1;else left = mid+1;}int left2, right2;if(target < nums[nums.size()-1]){left2 = left, right2 = nums.size()-1;while(left2 <= right2){mid = left2 + (right2-left2)/2;if(nums[mid] < target) left2 = mid+1;else if(nums[mid] > target) right2 = mid-1;else return mid;}}else if(target > nums[nums.size()-1]){left2 = 0, right2 = left-1;while(left2 <= right2){mid = left2 + (right2-left2)/2;if(nums[mid] < target) left2 = mid+1;else if(nums[mid] > target) right2 = mid-1;else return mid;}}else return nums.size()-1;return -1;}
};

这道题解决思路比较粗暴，首先按照上一题的解法求出最小元素的下标，然后将最后一个元素与target进行判断，如果target小于nums[n-1]那么再在最小元素的右边二分查找，反之则在最小元素的左边二分查找，所以我的解法使用了两次二分查找，ac了就偷懒每看解析了，解析肯定没这么复杂…

链表

反转链表

[传送门]( 206. 反转链表 - 力扣（LeetCode） )

解法一：双指针迭代

class Solution {
public:ListNode* reverseList(ListNode* head) {ListNode* cur = head, *pre = nullptr, *temp;while(cur != nullptr){temp = cur->next;cur->next = pre;pre = cur;cur = temp;}return pre;}
};

三个需要注意的点：①退出循环的条件②循环体第2，3，4条语句的顺序不能变③最后返回的是pre而不是cur，因为cur退出循环变成nullptr了

解法二：头插法

class Solution {
public:ListNode* reverseList(ListNode* head) {ListNode* res, *pMove = head;res = new ListNode();if(pMove == nullptr) return nullptr;while(pMove != nullptr){ListNode* s = new ListNode;s->val = pMove->val;s->next = res->next;res->next = s;pMove = pMove->next;}return res->next;}
};

按照实例的意思，它将所有元素都反序了，所以我们可以重新创建一个有头节点的链表采用头插法存取数据就能达到反转链表的效果。

反转链表II

[传送门]( 92. 反转链表 II - 力扣（LeetCode） )

class Solution {
public:ListNode* reverseBetween(ListNode* head, int left, int right) {ListNode* dummy = new ListNode(0, head), *p0 = dummy;for(int i = 0; i < left-1; i++){p0 = p0->next;}ListNode* pre = nullptr, *cur = p0->next, *temp;for(int i = 0; i < right-left+1; i++){temp = cur->next;cur->next = pre;pre = cur;cur = temp;}p0->next->next = cur;p0->next = pre;return dummy->next;}
};

这一题需要找到几个关键结点：①遍历开始前一个结点p0②遍历结束后cur和pre所指结点③设置一个哨兵结点指向head之前，用来作为返回值。遍历结束后p0->next->next一定指向cur，p0->next一定指向pre，而且两个书写顺序不能改变，题中所给的left和right就是边界值，就是我们循环的次数，中间反转链表与第一题相同采用双指针迭代的方法。最后注意为哨兵开辟空间的方法new ListNode(0, head);

二叉树

相同的树

[传送门]( 100. 相同的树 - 力扣（LeetCode） )

class Solution {
public:bool isSameTree(TreeNode* p, TreeNode* q) {if(p == nullptr || q == nullptr) return p == q;else{bool left = isSameTree(p->left, q->left);bool right = isSameTree(p->right, q->right);return p->val == q->val && left && right;}}
};

递归题还是得加强理解，现在能分析出递归的边界条件和各个限制条件，但是理解不了这些条件应该放在什么位置，这里递归退出条件写的十分妙，如果是其中一个为nullptr那么返回false，如果都为空那么返回true，如果都为真，那么就继续递归，返回的是当前两个结点val是否相等&&左子树是否相等&&右子树是否相等，自己写的时候没有考虑到当前结点的val是否相等就导致的错误。

对称二叉树

[传送门]( 101. 对称二叉树 - 力扣（LeetCode） )

class Solution {
public:bool isSameTree(TreeNode* p, TreeNode* q){if(p == nullptr || q == nullptr) return p == q;return p->val == q->val && isSameTree(p->left, q->right) && isSameTree(p->right, q->left);}bool isSymmetric(TreeNode* root) {return isSameTree(root->left, root->right);}
};

其实这一题和上一题十分相似，只是我们需要换个角度思考一下问题，判断两个树是否相等就是判断当前p、q所指val是否相等&&p左子树是否等于q左子树&&p右子树是否等于q右子树。而看一个树是否对称也就是方向的不同，其他与判断两个树是否相等是一个意思。所以判断对称二叉树的条件是：p、q所指val是否相等&&p左子树是否等于q右子树&&p右子树是否等于q左子树。由于该题函数只有一个root参数，所以我们需要另外写一个函数用来调用即可。

平衡二叉树

[传送门]( 110. 平衡二叉树 - 力扣（LeetCode） )

class Solution {
public:int getHeight(TreeNode* p){if(p == nullptr) return 0;return max(getHeight(p->left), getHeight(p->right)) + 1;}bool isBalanced(TreeNode* root) {if(root == nullptr) return true;else{int x = getHeight(root->left)-getHeight(root->right);if( x >= -1 && x <= 1) return isBalanced(root->left) && isBalanced(root->right);//abs(x)等价于x >= -1 && x <= 1else return false;}}
};

这道题是自己独立ac的，就没有看其他的解题思路了。说说我的理解：首先平衡二叉树的定义为该树的所有结点的左右子树深度差不超过1，也就是绝对值小于等于1。首先采用递归的写法定义一个求结点深度的函数，然后再在主函数中递归调用。

二叉树的右视图

[传送门]( 199. 二叉树的右视图 - 力扣（LeetCode） )

class Solution {
public:vector<int> ans = {};void f(TreeNode* root, int depth){if(root == nullptr) return;else{if(ans.size() == depth){ans.push_back(root->val);}f(root->right, depth+1);f(root->left, depth+1);}}vector<int> rightSideView(TreeNode* root) {f(root, 0);return ans;}
};

真的是看了大神的题解就是能豁然开朗，做题不能仅仅局限于bfs或者dfs，官方就是用这两种解法看起来相当复杂，因为单纯用那两种方法需要考虑的东西太多，理解起来也就费劲。右视图也就是保存这棵树每一层的最右边一个结点，如何将这个问题比较好的转化成代码呢？定义一个存储结点的数组和一个新函数，函数参数包括结点指针和深度，只要在函数体用一条判断数组长度是否等于树深度就能知道这个结点该不该存在数组里，除此之外，必须要保证该函数一定是先递归的右子树再递归左子树，这样才能保证是每一层的最右边结点存入的数组。这里便于理解就将根节点的深度和数组长度都初始化为0。

验证二叉搜索树

[传送门]( 98. 验证二叉搜索树 - 力扣（LeetCode） )

class Solution {
public:bool examTree(TreeNode* root, long l_limit, long r_limit){if(root == nullptr) return true;else{if(root->val > l_limit && root->val < r_limit){return examTree(root->left, l_limit, root->val) && examTree(root->right, root->val, r_limit);}return false;}}bool isValidBST(TreeNode* root) {return examTree(root, LONG_MIN, LONG_MAX);}
};

首先要仔细解读题目中所给的二叉搜索树的定义，这些定义就是用来限制的条件，所以我们每当访问一个根节点的时候只需要判断其是否在这个范围之内就行。再就是怎么将这个边界往下传，只需定义一个函数参数分别是root指针和左右边界就行了，每次递归左子树就更新右边界、递归右子树就更新左边界，直到遇到了空结点就表明之前的递归都满足条件，那么就返回true。

二叉树的最近公共祖先

[传送门]( 236. 二叉树的最近公共祖先 - 力扣（LeetCode） )

class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == nullptr || root == p || root == q){return root;}TreeNode* l_left = lowestCommonAncestor(root->left, p, q);TreeNode* l_right = lowestCommonAncestor(root->right, p, q);if(l_left && l_right){return root;}return l_left ? l_left : l_right;}
};

这道题没写出来有两个问题：①读题不仔细：没有从给出的代码中发现p和q是指针类型的②这一道题其实能偶通过分类讨论分析出递归的思路。

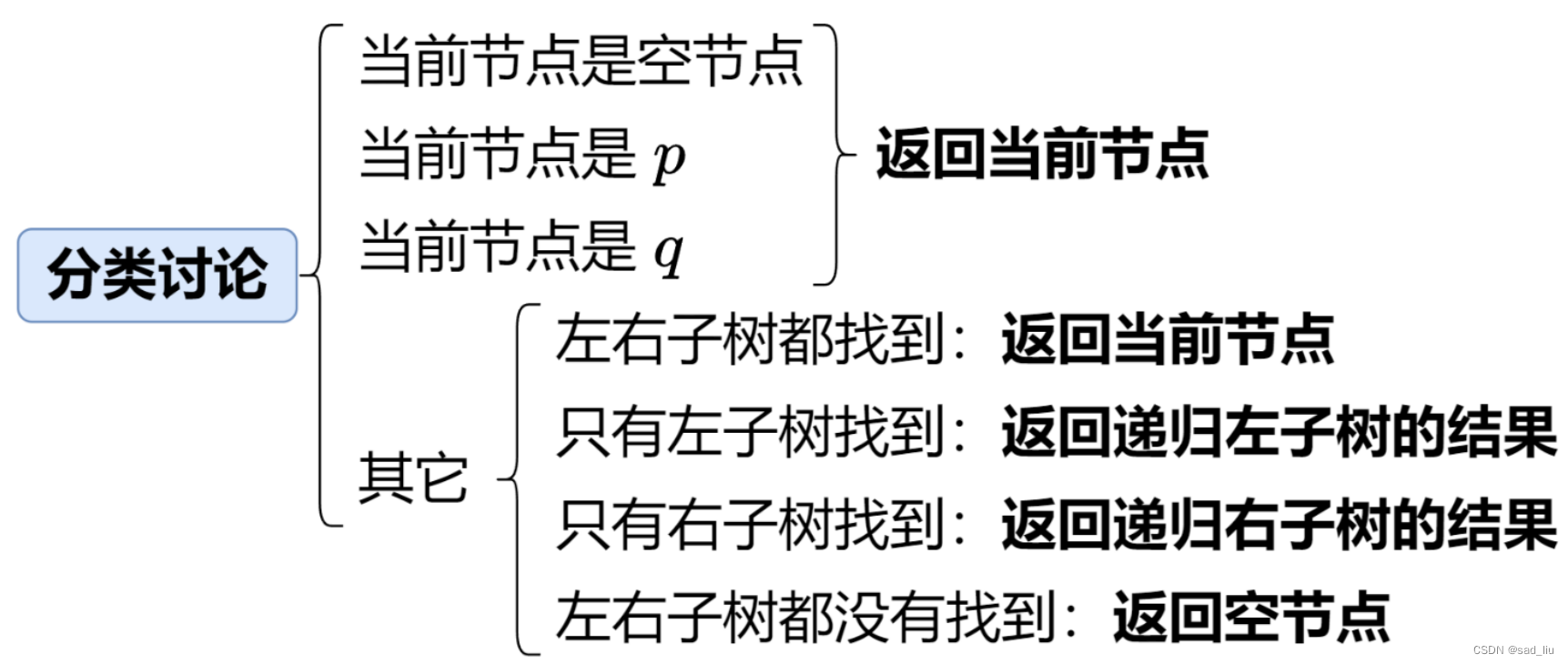
还有，我什么时候才能像题解一样写出这么简洁的题解啊555…分类讨论的形式在代码中能很明白的体现出来，这就是大神的威力啊，狠狠膜拜了。

二叉搜索树的最近公共祖先

[传送门]( 235. 二叉搜索树的最近公共祖先 - 力扣（LeetCode） )

class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root->val < p->val && root->val < q->val){return lowestCommonAncestor(root->right, p, q);}else if(root->val > p->val && root->val > q->val){return lowestCommonAncestor(root->left, p, q);}return root;}
};

这一题刚开始看的时候我发现其实跟上一题的解法可以完全相同，然后我就重新默写了一遍上一题的代码而且能ac，但我仔细一想这一题肯定有不同的解法。题干中写到这是一颗二叉搜索树，我就在想二叉搜索树会有什么性质呢？我想到的是它的中序遍历是一个升序的序列，所以我在想是不是只要递归出第一个处于[p->val,q->val]之间的数，那个数对应的root值就是我想要的答案，结果是我写不出代码。。。看了题解之后发现是从另一角度出发思考的：根节点值严格大于左子树的所有值&&根节点值严格小于右子树所有值，又因为题干中给出p和q是一定存在的，所以整个题只需要分三部分考虑：①根节点值都小于p和q的值，递归右子树②根节点值都大于p和q的值，递归左子树③其他情况返回root根节点即可。

二叉树层序遍历

[传送门]( 102. 二叉树的层序遍历 - 力扣（LeetCode） )

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {if(root == nullptr) return {};//没有考虑特殊情况，测试样例不能通过vector<vector<int>> v;queue<TreeNode*> q;q.push(root);while(!q.empty()){vector<int> temp;int n = q.size();for(int i = 0; i < n; i++){if(q.front()->left) q.push(q.front()->left);if(q.front()->right) q.push(q.front()->right);temp.push_back(q.front()->val);q.pop();}v.push_back(temp);}return v;}
};

这一道题唯一卡住我思路的地方就是返回的是一个二维数组，如果是一个一维数组，那很好办用一个队列即可。可是这里的二维数组硬是卡着我不知道怎么打码，仔细点来说就是我不知道如何按层存取二叉树里的元素。看了一眼解决方法我就直到如何写了，脑子就是一时间转不过来，唉。方法就是嵌套循环，外层循环是队列为空退出为条件，内层循环只需遍历该层的个数次就行了。可是这么写少考虑到了一种情况，也就是如果该二叉树为空，循环里面会报错(出现空指针的操作)导致测试用例不能通过，不要问是谁漏了，问就是我漏了。

二叉树的锯齿形层序遍历

[传送门]( 103. 二叉树的锯齿形层序遍历 - 力扣（LeetCode） )

自己写的：

class Solution {
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {if(root == nullptr) return {};deque<TreeNode*> d;vector<vector<int>> v;d.push_back(root);int flag = 1;//1表示从左往右，-1表示从右往左while(!d.empty()){int n = d.size(), i;vector<int> temp;if(flag == 1){for(i = 0; i < n; i++){if(d.front()->left) d.push_back(d.front()->left);if(d.front()->right) d.push_back(d.front()->right);temp.push_back(d.front()->val);d.pop_front();}}else if(flag == -1){for(i = 0; i < n; i++){if(d.back()->right) d.push_front(d.back()->right);if(d.back()->left) d.push_front(d.back()->left);temp.push_back(d.back()->val);d.pop_back();}}v.push_back(temp);flag = -flag;}return v;}
};

大佬写的：

class Solution {
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {if(root == nullptr) return {};vector<vector<int>> v;queue<TreeNode*> q;q.push(root);for(int flag = false; !q.empty(); flag = !flag){vector<int> temp;for(int i = q.size(); i > 0; i--){TreeNode* node = q.front();if(node->left) q.push(node->left);if(node->right) q.push(node->right);temp.push_back(node->val);q.pop();}if(flag) reverse(temp.begin(), temp.end());v.push_back(temp);}return v;}
};

大佬写的代码就是简洁高效啊，实在是佩服。我的代码的思路是：想到这题和二叉树层序遍历之间只多了一个遍历顺序的条件，所以我就先按照层序遍历的写法写，flag是用来判断该层是用从左往右还是从右往左，还有，考虑到需要一个数据结构能对其进行两端操作的队列，这里我就用到了双端队列，它能对首尾插入和删除。

再看到优化的代码：第一个循环用的for，这是我从未见过的一种写法，是在是巧妙，就相当于我的while和if条件写在一起了。再就是存取每层数据时它不是对队列进行改变，而是对临时数组进行反转函数reverse，它用一行代替了我两个for循环，天呐这这么想到的…

本人就爱写点发牢骚的话hahahaha反正也没什么人看。

找树左下角的值

[传送门]( 513. 找树左下角的值 - 力扣（LeetCode） )

自己的解法：

class Solution {
public:vector<vector<int>> orderResearch(TreeNode* root){vector<vector<int>> v;queue<TreeNode*> q;q.push(root);while(!q.empty()){vector<int> temp;for(int i = q.size(); i > 0; i--){TreeNode* node = q.front();if(node->left) q.push(node->left);if(node->right) q.push(node->right);temp.push_back(node->val);q.pop();}v.push_back(temp);}return v;}int findBottomLeftValue(TreeNode* root) {vector<vector<int>> v = orderResearch(root);return v[v.size()-1][0];}
};

想到前两题返回的都是层序遍历的结果，我就在想，树左下角的值不就是最后一层的第一个值吗，我就重新写了一个层序遍历的函数并返回二维数组，结果就是v[v.size()-1] [0]。v.size()的值表示v的行数

解法二：

class Solution {
public:int findBottomLeftValue(TreeNode* root) {queue<TreeNode*> q;TreeNode* node;q.push(root);while(!q.empty()){node = q.front();if(node->right) q.push(node->right);if(node->left) q.push(node->left);q.pop();}return node->val;}
};

看上去就是普通的层序遍历吗？不，这里不同在两个if的顺序，我们正常的层序遍历是从左至右所以是先node->left再node->right，这样最后一个元素是最右下角的元素，该题是要求出最左下角的元素，那么我们只需要改两个if条件的顺序就能达到题目的意思啦

解法三：

class Solution {
public:vector<int> v = {};void func(TreeNode* root, int depth){if(root == nullptr) return;if(depth == v.size()){v.push_back(root->val);}func(root->left, depth+1);func(root->right, depth+1);}int findBottomLeftValue(TreeNode* root) {func(root, 0);return v[v.size()-1];}
};

这个解法来自于评论区的朋友，看到了这样的评论"可以考虑二叉树的左视图，然后返回左视图的最后一个元素"，左视图？怎么这么熟悉，哦！原来我写过右视图，然后我大脑迅速运转回顾右视图该怎么写，由于参数的限定，这里需要重新定义一个函数和一个全局的数组v并初始化为空，函数的参数为root指针和整形depth表示该层的深度(这个depth是跟着递归的，递归到那一层depth也就跟着更新，这里我写的时候没有想到，我将depth也设置为全局变量结果输出的是树中最后一个元素…还是细节决定成败啊)，然后就是先调用root->left再调用root->right因为左视图优先看到的是左子树，所以先遍历左子树哦！