送给大家一句话：

那脑袋里的智慧，就像打火石里的火花一样，不去打它是不肯出来的。——莎士比亚

今天我学习了滑动窗口的算法思路，接下来请与我一起看看吧！！！

认识滑动窗口

滑动窗口问题可以说是一种特殊的双指针问题，通常用于解决以下类型的问题：

1. 连续子数组或子字符串问题：例如，找出一个数组中连续元素和最大或最小的子数组，或者在字符串中找到一个包含特定字符的最短子字符串。
2. 固定窗口大小问题：当窗口大小固定时，我们可以通过移动窗口来遍历整个数组或字符串，并记录所需的统计信息。
3. 可变窗口大小问题：在某些情况下，窗口的大小可能会根据特定条件而变化。这需要我们在遍历过程中动态地调整窗口的大小。

滑动窗口算法的基本思想是使用双指针（有时也可能使用更多指针）来表示窗口的边界。在每一步中，我们可以根据特定条件来移动窗口的边界，并更新所需的统计信息。

看这些定义是真无法想象出来哦怎么个滑动窗口的，下面我们一起来做题吧：

Leetcode 209. 长度最小的子数组

题目描述

看这个题目还是很好理解的，只需要我们找到和大于target的连续子数组，我们来看第一个样例target = 7, nums = [2,3,1,2,4,3] 显然4,3是最小的子数组。接下来分析一下算法思路：

算法思路

根据题目要求，首先可以想到的是暴力枚举算法（遇事不决，暴力解决），遍历穷举出所有的连续子数组，寻找满足要求的子数组，最终就找到了最小的连续子数组：

class Solution {
public:int minSubArrayLen(int s, vector<int>& nums) {//暴力解法int n = nums.size();if (n == 0) {return 0;}//默认为最大值int ans = INT_MAX;//开始遍历for (int i = 0; i < n; i++) {//重置sum值int sum = 0;//判断子数组是否满足for (int j = i; j < n; j++) {sum += nums[j];if (sum >= s) {//满足就更新结果ans = min(ans, j - i + 1);break;}}}return ans == INT_MAX ? 0 : ans;}
};

这样暴力的算法的时间复杂度是O(n^2),我们看看可不可以进行优化：
来看图解（来着力扣官方）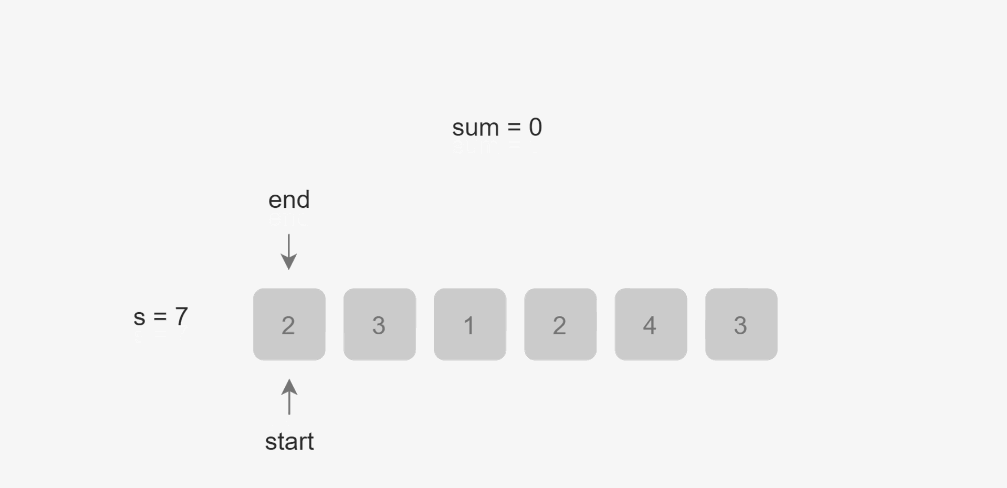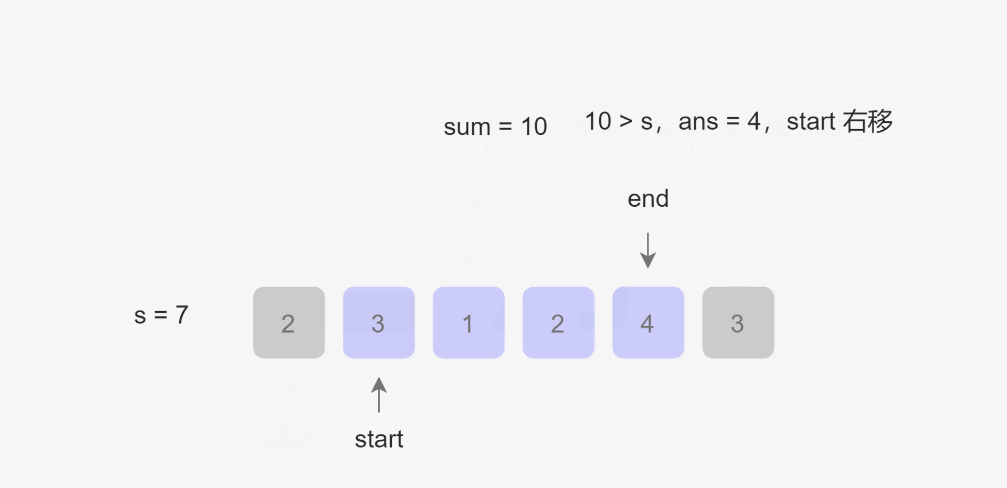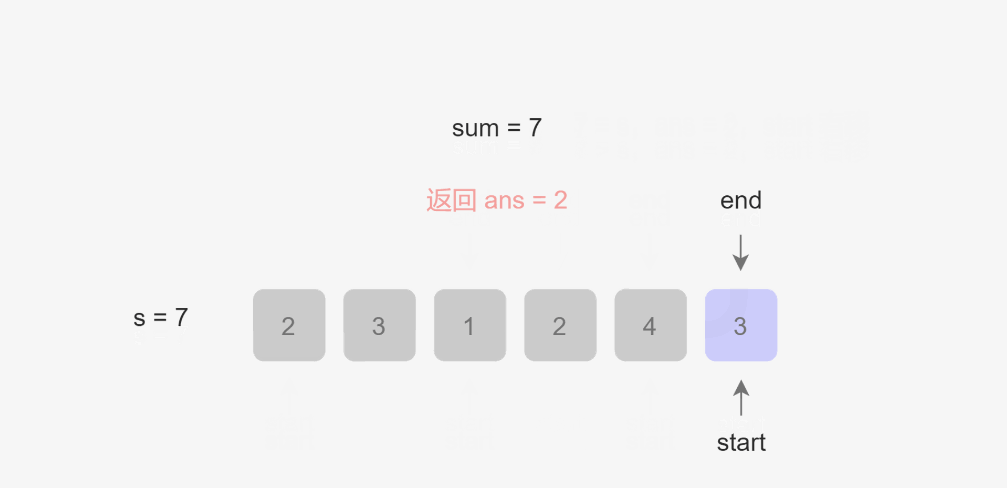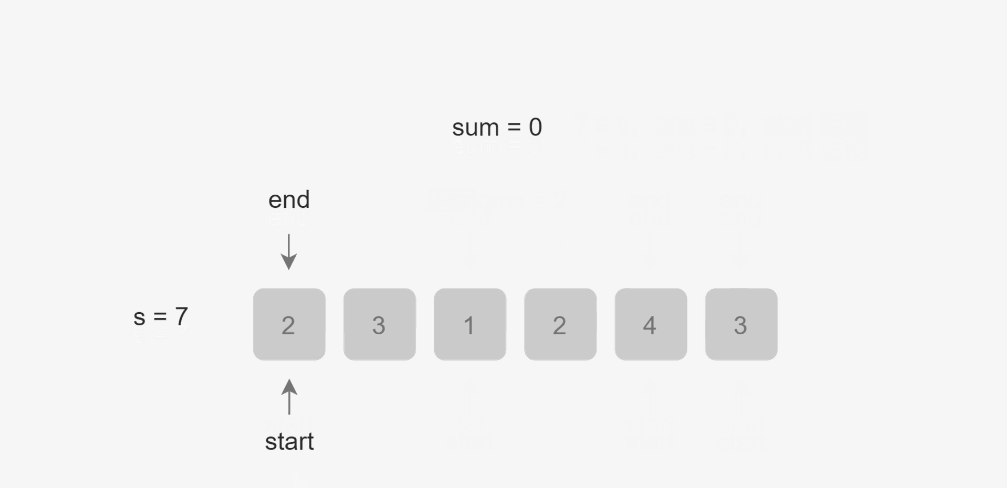

这样就模拟了滑动窗口：
做法：将右端元素划⼊窗⼝中，统计出此时窗⼝内元素的和：

• 如果窗⼝内元素之和⼤于等于 target ：更新结果，并且将左端元素划出去的同时继续判
  断是否满⾜条件并更新结果（因为左端元素可能很⼩，划出去之后依旧满⾜条件）
• 如果窗⼝内元素之和不满⾜条件： right++ ，另下⼀个元素进⼊窗⼝。

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int left = 0,right = 0;//设置为最大值 保证没有满足的子数组时可以判断int len = INT_MAX;int sum = 0;sum += nums[left];while(left < nums.size() && right < nums.size()){//if(sum < target ){right++;if(right < nums.size())sum += nums[right];}while (sum >= target){len = min (right - left + 1 , len) ;sum -= nums[left];left++;}}return len == INT_MAX ? 0:len;}
};

这样大大提高了算法的效率！！！
为何滑动窗⼝可以解决问题，并且时间复杂度更低？

1. 这个窗⼝寻找的是：以当前窗⼝最左侧元素（记为 left1 ）为基准，符合条件的情况。也就是在这道题中，从 left1 开始，满⾜区间和 sum >= target 时的最右侧（记为right1 ）能到哪⾥。
2. 我们既然已经找到从 left1 开始的最优的区间，那么就可以⼤胆舍去 left1 。但是如果继续像⽅法⼀⼀样，重新开始统计第⼆个元素（ left2 ）往后的和，势必会有⼤量重复的计算（因为我们在求第⼀段区间的时候，已经算出很多元素的和了，这些和是可以在计算下次区间和的时候⽤上的）。
3. 此时， rigth1 的作⽤就体现出来了，我们只需将 left1 这个值从sum 中剔除。从right1 这个元素开始，往后找满⾜ left2 元素的区间（此时right1 也有可能是满⾜的，因为 left1 可能很⼩。 sum 剔除掉 left1 之后，依旧满⾜⼤于等于target ）。这样我们就能省掉⼤量重复的计算。

这样我们不仅能解决问题，⽽且效率也会⼤⼤提升

继续我们来看下一题

Leetcode 3. 无重复字符的最长子串

题目描述

描述也是十分简单奥，我们接着来看如何解决

算法思路

首先想到的还是暴力枚举啊，我们可以借助哈希表来确定是否重复。
枚举过程中就会发现左右指针移动方向相同，所以可以进行滑动窗口

1. 入窗口（右指针移动）
2. 判断（判断是否需要移动左指针）
3. 出窗口
4. 更新结果

class Solution {
public:int lengthOfLongestSubstring(string s) {int len = 0;int n = s.size();//使用哈希进行判断是否重复int hash[128] = {0};int ret = 0;for(int left = 0,right = 0; right < n; right++){//进入窗口hash[s[right]]++;//判断while(hash[s[right]] > 1){//出窗口hash[s[left]]--;left++;len--;}//更新结果len++;ret = max(len,ret);}return ret;}
};

这样就完美解决。
其实滑动窗口都是可以套用上面的模版的，不信？来看下一题

Leetcode 1004. 最大连续1的个数 III

题目描述

题目描述依然简单奥，只是判断条件发生了改变，我们需要来定义一个数字来比较是否满足少于k

算法思路

依旧是：

1. 入窗口（右指针移动）
2. 判断（判断是否需要移动左指针）
3. 出窗口
4. 更新结果

class Solution {
public:int longestOnes(vector<int>& nums, int k) {int tmp = 0,left = 0,right = 0,n = nums.size();int ret = 0;while(right < n){if(nums[right] == 0) {tmp++;    }while(tmp > k){if(nums[left] == 0) tmp--;left++;}ret = max(ret,right - left + 1);right++;}return ret;}
};

这样就成功完成解题！！！

总结

滑动窗口问题是可以通过模版来解决：

1. 入窗口（右指针移动）
2. 判断（按题分析判断是否需要移动左指针）
3. 出窗口
4. 更新结果

这样基本滑动窗口都可以解决，但重要的是理解滑动窗口的思路是如何得到的，是如何从暴力算法优化出来的。

送给大家一句话：

那脑袋里的智慧，就像打火石里的火花一样，不去打它是不肯出来的。——莎士比亚

Thanks♪(･ω･)ﾉ谢谢阅读！！！

下一篇文章见