目录
十八、二分查找
114. 搜索插入位置 ① √-
115. 搜索二维矩阵 ②
116. 寻找峰值 ② √-
117. 搜索旋转排序数组 ②
118. 在排序数组中查找元素的第一个和最后一个位置 ② √
119. 寻找寻钻排序数组中的最小值 ②
120. 寻找两个正序数组的中位数 ③
136. 直线上最多的点数 ③
十八、二分查找
114. 搜索插入位置 ① √-
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5 输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2 输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7 输出: 4
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums为 无重复元素 的 升序 排列数组-104 <= target <= 104
方法1:(0ms)
public static int searchInsert(int[] nums, int target) {int left = 0;int right = nums.length - 1;while (left <= right){int mid = (left + right) / 2;if (target > nums[mid]){left = mid + 1;}else if (target < nums[mid]){right = mid - 1;}else {return mid;}}return left;}115. 搜索二维矩阵 ②
给你一个满足下述两条属性的 m x n 整数矩阵:
- 每行中的整数从左到右按非严格递增顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
示例 1:

输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 输出:true
示例 2:
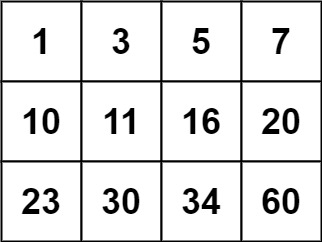
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
方法1:(100%)
public static boolean searchMatrix(int[][] matrix, int target) {int rows = matrix.length;int left = 0;int right = rows - 1;if (rows > 1) {while (left < right) {int mid = left + (right - left + 1) / 2;if (target < matrix[mid][0]) {right = mid - 1;} else if (target > matrix[mid][0]) {left = mid + 1;} else {return true;}}}int min = 0;int max = matrix[0].length - 1;if (max > 0) {while (min <= max) {int newMid = min + (max - min + 1) / 2;if (target < matrix[left][newMid]) {max = newMid - 1;} else if (target > matrix[left][newMid]) {min = newMid + 1;} else {return true;}}} else {if (target == matrix[0][0]) {return true;} else {return false;}}return false;}其他解法:. - 力扣(LeetCode)
116. 寻找峰值 ② √-
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]输出:2 解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4] 输出:1 或 5 解释:你的函数可以返回索引 1,其峰值元素为 2;或者返回索引 5, 其峰值元素为 6。
提示:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1- 对于所有有效的
i都有nums[i] != nums[i + 1]
方法1:(0ms)
public int findPeakElement(int[] nums) {if (nums.length == 1){return 0;}if (nums.length == 2){if (nums[0] > nums[1]){return 0;}else {return 1;}}int max = 0;for (int i = 1; i < nums.length - 1; i++) {if (nums[i] > nums[i - 1]){if (nums[i] > nums[i + 1]){return i;}else {max = i;}}}return max;}
方法2:(0ms)

public int findPeakElement(int[] nums) {int left = 0, right = nums.length - 1;for (; left < right; ) {int mid = left + (right - left) / 2;if (nums[mid] > nums[mid + 1]) {right = mid;} else {left = mid + 1;}}return left;}作者:画手大鹏
链接:https://leetcode.cn/problems/find-peak-element/solutions/6695/hua-jie-suan-fa-162-xun-zhao-feng-zhi-by-guanpengc/
117. 搜索旋转排序数组 ②
118. 在排序数组中查找元素的第一个和最后一个位置 ② √
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1]
示例 3:
输入:nums = [], target = 0 输出:[-1,-1]
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums是一个非递减数组-109 <= target <= 109
方法1:(0ms)
public static int[] searchRange(int[] nums, int target) {int left = 0;int right = nums.length - 1;int[] res = new int[]{-1,-1};while (left <= right){int mid = (left + right) / 2;if (target < nums[mid]){right = mid - 1;}else if (target > nums[mid]){left = mid + 1;}else {int i = mid, j = mid;while (i > -1 && nums[i] == target){i--;}res[0] = ++i;while (j < nums.length && nums[j] == target){j++;}res[1] = --j;return res;}}return res;}