对于二叉树而言,如果不是完全二叉树,就不再适合用数组存储了

在任意二叉树中，度为0的节点都比度为2的节点多1个，即 n0 = n2 + 1

二叉树结构

typedef struct BinTreeNode
{int val;struct BinTreeNode* left;struct BinTreeNode* right;
}BTNode;

二叉树的遍历

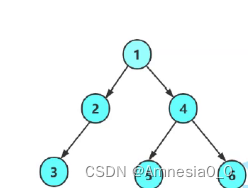
                顺序                                访问顺序(n = NULL)

1.前序      根,左子树,右子树        1 2 3 n n n 4 5 n n 6 n n

2.中序      左子树,根,右子树        n 3 n 2 n 1 n 5 n 4 n 6 n 

3.后序      左子树,右子树,根        n n 3 n 2 n n 5 n n 6 4 1

4.层序                                         1 2 4 3 5 6 

1.前序遍历

通过递归,可以将一颗树拆解为许多棵树(直到root为空为止),是根就访问,不是,就向下走

void PreOrder(BTNode* root)
{if (root == NULL){return;}printf("%d\n", root->val);PreOrder(root->left);PreOrder(root->right);
}

2.中序遍历

同理,是左子树(该左子树不能有任何其他子树,否则就是根),就访问,不是就向下

void InOrder(BTNode* root)
{if (root == NULL){return;}PreOrder(root->left);printf("%d\n", root->val);PreOrder(root->right);
}

3.后序遍历

同理

void PostOrder(BTNode* root)
{if (root == NULL){return;}PreOrder(root->left);PreOrder(root->right);printf("%d\n", root->val);
}

4.求二叉树的大小

通过递归,将所有左子树和右子树节点遍历,再加上根本身,就是总节点数,它的本质是二叉树的后序遍历(走完根后结束)(必须将左右子树全部走完才能求出树的大小,因此一定是后序)

int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

5.求第k层的节点个数

分割子问题 : 从第一层起的第k层的节点个数 = 第二层起的第k - 1层的节点个数

一直递归,每递归一次,k - 1,第k层时k = 1

int TreeLevel(BTNode* root, int k)
{asssert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}//不为空且k>0说明第k层的节点再子树里return TreeLevel(root->left, k - 1) + TreeLevel(root->right, k - 1);
}

6.查找值为x的节点

注意:要保证函数存在返回值

BTNode* TreeFind(BTNode* root, int x)
{if (root == NULL){return NULL;}if (root->val == x){return root;}//在左树中找,找到返回BTNode* ret1 = TreeFind(root->left, x);if (ret1 != NULL){return ret1;}//在右树中找,找到返回BTNode* ret2 = TreeFind(root->right, x);if (ret2 != NULL){return ret2;}//树中没有x节点return NULL;
}

typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);//pi是下标
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);

BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{if (a[*pi] == '#')//#代表空的位置//pi是下标{(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->_data = a[*pi];root->_left = BinaryTreeCreate(a, pi);//前序递归root->_right = BinaryTreeCreate(a, pi);return root;
}void BinaryTreeDestory(BTNode** root)
{if (*root == NULL){return;}BinaryTreeDestory(&(*root)->_left);BinaryTreeDestory(&(*root)->_right);free(*root);*root = NULL;
}int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right) + 1;
}int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;return root->_left == NULL && root->_right == NULL ?BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right) + 1 :BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->_data == x)return root;//在左树BTNode* ret1 = BinaryTreeFind(root->_left, x);if (ret1 != 0)return ret1;//在右树BTNode* ret2 = BinaryTreeFind(root->_right, x);if (ret2 != 0)return ret2;//找不到return NULL;
}void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL)return;printf("%d\n", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}void BinaryTreeInOrder(BTNode* root)
{if (root == NULL)return;BinaryTreeInOrder(root->_left);printf("%d\n", root->_left);BinaryTreeInOrder(root->_right);
}void BinaryTreePostOrder(BTNode* root)
{if (root == NULL)return;BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%d\n", root->_left);
}void BinaryTreeLevelOrder(BTNode* root)
{if (root == NULL)return;Queue temp;QueueInit(&temp);//先将根放入队列if(root != NULL){QueuePush(&temp, root);}//直到队列为空为止,出根,入左右子树while (QueueEmpty(&temp)){BTNode* front = QueueFront(&temp);QueuePop(&temp);printf("%d\n", front->_data);if (root->_left != NULL){QueuePush(&temp, root->_left);}if (root->_right != NULL){QueuePush(&temp, root->_right);}}QueueDestroy(&temp);
}int BinaryTreeComplete(BTNode * root){Queue qu;BTNode* cur;int tag = 0;QueueInit(&qu);QueuePush(&qu, root);while (!QueueIsEmpty(&qu)){cur = QueueTop(&qu);putchar(cur->_data);if (cur->_right && !cur->_left){return 0;}if (tag && (cur->_right || cur->_left)){return 0;}if (cur->_left){QueuePush(&qu, cur->_left);}if (cur->_right){QueuePush(&qu, cur->_right);}else{tag = 1;}QueuePop(&qu);}QueueDestroy(&qu);return 1;}