【数据结构与算法】(14)：堆排序和选择排序（超详细配图~）

🤡博客主页：Code_文晓

🥰本文专栏：数据结构与算法

😻欢迎关注：感谢大家的点赞评论+关注，祝您学有所成！

✨✨💜💛想要学习更多数据结构与算法点击专栏链接查看💛💜✨✨

1. 选择排序的概念和思想

前面我们一起学习了插入类排序《插入排序和希尔排序看这一篇文章就够了！》和交换类排序《交换排序之冒泡排序和快速排序》，这次，我们学习一个新的排序种类——选择类排序。

选择类排序 是一种基于比较的排序算法，他的基本思想就是每一趟在待排序的元素中选取关键字最小（或最大）的元素加入到有序子序列中。而简单选择排序则是选择类排序中的一种。

基本思想：每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

2. 简单选择排序

在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素
若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个）元素交换
在剩余的array[i]--array[n-2]（array[i+1]--array[n-1]）集合中，重复上述步骤，直到集合剩余1个元素

下面是简单选择排序的动态图效果：

有了动态图，下面一步步来演示简单选择排序的过程，如图1所示：

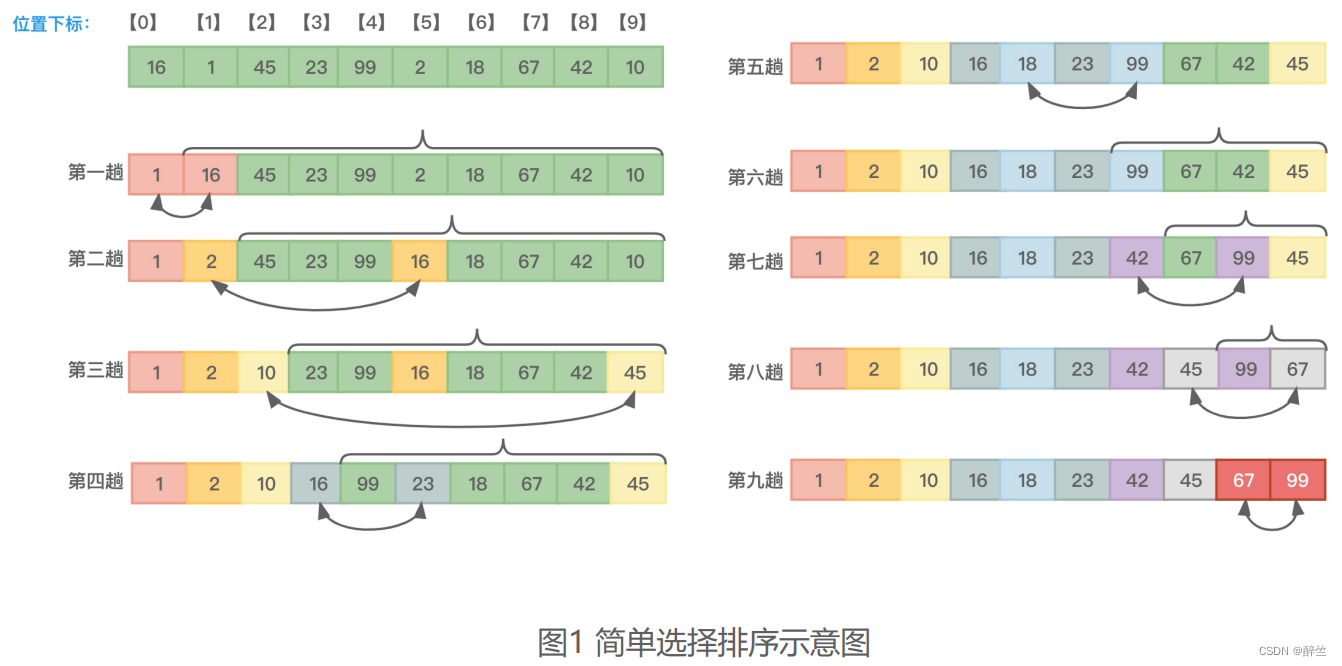
图1左上侧是待排序的10个元素，我们以从小到大排序来说明。

第一趟排序：从待排序的元素中找出值最小的元素和下标为0的元素做交换，这样下标为0的位置所保存的就是最小值的元素，此时无需再理会下标为0的位置。
第二趟排序：抛开下标为0位置的元素，从其余元素中找出值最小的元素和下标为1的元素做交换，这样下标为1位置所保存的就是剩余待排序元素中最小值的元素，此时无需再理会下标为1的位置。
第三趟排序：抛开下标为0、1位置的元素，从其余元素中找出值最小的元素和下标为2的元素做交换，这样下标为2位置所保存的就是剩余待排序元素中最小值的元素，此时无需再理会下标为2的位置。
如此重复，第九趟排序：抛开下标为0、1、2、3、4、5、6、7位置的元素，从其余元素中找出值最小的元素和下标为8的元素做交换，这样下标为8位置所保存的就是剩余待排序元素中最小值的元素。此时，下标为9的元素自然就是值最大的元素。

到这里，整个简单选择排序算法就完成了。下面是的代码实现：

template<typename T>
void Swap(T* p1, T* p2)
{T tmp = *p1;*p1 = *p2;*p2 = tmp;
}//简单选择排序（从小到大）
template<typename T>
void SelectSort(T myarray[], int length)
{for (int i = 0; i < length - 1; ++i) //一共要进行length-1趟{int minidx = i;  //保存最小元素位置//在myarray[i]到myarray[length-1]中选择最小值for (int j = i + 1; j < length; ++j){if (myarray[j] < myarray[minidx])minidx = j; //保存最小元素值位置} //end for jif (minidx != i){Swap(&myarray[i], &myarray[minidx])}} //end for ireturn;
}

简单选择排序的优化 :

//简单选择排序优化（从小到大）
template<typename T>
void SelectSort(T myarray[], int length)
{int begin = 0, end = length- 1;while (begin < end){int maxidx = begin, minidx = begin;for (int i = begin; i <= end; i++){if (myarray[i] > myarray[maxidx]){maxidx = i;}if (myarray[i] < myarray[minidx]){minidx = i;}}Swap(&myarray[begin], &myarray[minidx]);if (begin == maxidx){maxidx = minidx;}Swap(&myarray[end], &myarray[maxidx]);++begin;--end;}
}

该算法的时间复杂度如何呢？我们用n代表元素数量，无论原有数据是否有序，都需要进行n-1趟处理，总共需要对比的关键字次数是(n-1)+(n-2)+…+1= $\frac{n(n-1)}{2}$ 次（等差数列求和公式）。而需要元素交换的次数最少为0次，最多也不会超过3(n-1)次。所以简单选择排序算法的时间复杂度为O( $n^{2}$ )。空间复杂度为O(1)。

此外，该算法是不稳定的，只需要用一组数据2、2、1测试一下即可知道。如图2所示，前两个元素在排好序之后位置已经调换了。

3. 堆排序

简单选择排序说完之后，我们来说一下堆排序。这两类排序都属于选择类排序，不过两者的实现方式不同。简单选择排序是每趟从待排序的元素中找出值最小的元素放到已排序序列的末尾，直到所有元素排序完成。而堆排序是通过将待排序元素构成一个堆的方式来实现元素的排序，可以说，堆排序的效率往往更高。

其实在本专栏中的这篇文章详细讲解了堆的概念性质和操作，其中在堆的应用中堆排序已经讲解的很详细了，大家可以看看这个文章《”堆“和二叉树顺序存储的”缘“》。既然我们学习到了排序专题，这里换一些配图和数据重新讲一下，大家也可以将两个内容对比一下学习，加强记忆。

堆的基本概念

堆是有序的完全二叉树，这里所说的有序指的是父节点一定大于等于子节点值或者父节点一定小于等于子节点值。

根据概念可知，堆又分为大根堆和小根堆：

大根堆（大顶堆/最大堆）：每个结点的值都大于或等于其左右孩子结点的值

小根堆（小顶堆/最小堆）：每个结点的值都小于或等于其左右孩子结点的值

我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中：

该数组从逻辑上讲就是一个堆结构，这篇文章《树与二叉树的概念、性质及详细证明》学习过的二叉树的性质六我们知道：

性质六：对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则编号为i的节点有：

若 i>0，i 位置节点的双亲序号：(i-1)/2；（若 i=0，i则是根节点的编号，无双亲节点）
若 2i+1<n，左孩子序号：2i+1；（2i+1>=n否则无左孩子）
若 2i+2<n，右孩子序号：2i+2；（2i+2>=n否则无右孩子）

所以将堆的逻辑结构映射到数组中，我们用上述性质六的公式重新来描述一下堆的定义就是：

大根堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小根堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2

如果实现从小到大的排序算法，则使用大顶堆比较方便，实现出的算法占用的辅助空间更少。如果实现从大到小排序，则使用小顶堆比较方便。

堆排序就是利用堆（大顶堆或者小顶堆）进行排序的方法。这里我将采用大顶堆来实现。

堆排序的基本思想是：把待排序的n个元素的序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将该节点数据删除，实际是将该节点数据与堆待排序序列末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素的序列重新构造成一个大顶堆，这样会得到n个元素的次大值。如此反复执行，便能得到一个有序序列了。

所以，堆排序需要解决两个主要问题。

由一个无序序列建成一个堆。
在输出堆顶元素（删除元素）后，对其余元素进行调整从而生成一个新堆。

1、构造初始堆

将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

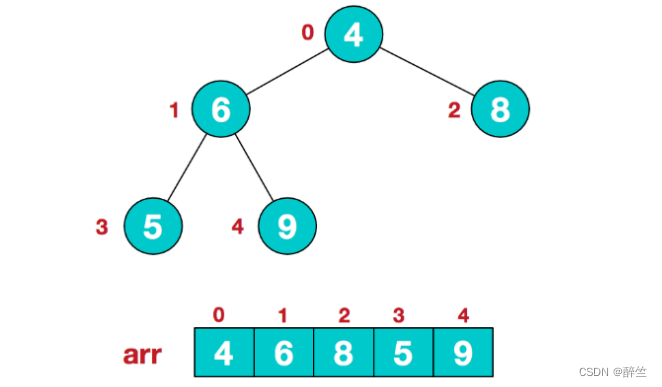
2、此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点为 $arr.length/2-1=5/2-1=1$ ，也就是下标为1的节点6），从左至右，从下至上进行调整。

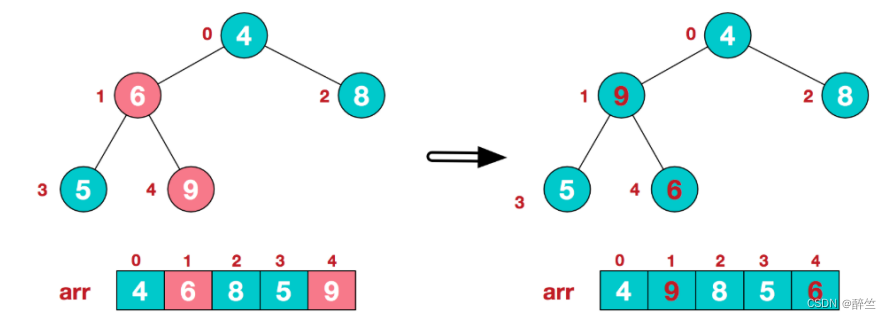
3、找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换

4、这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

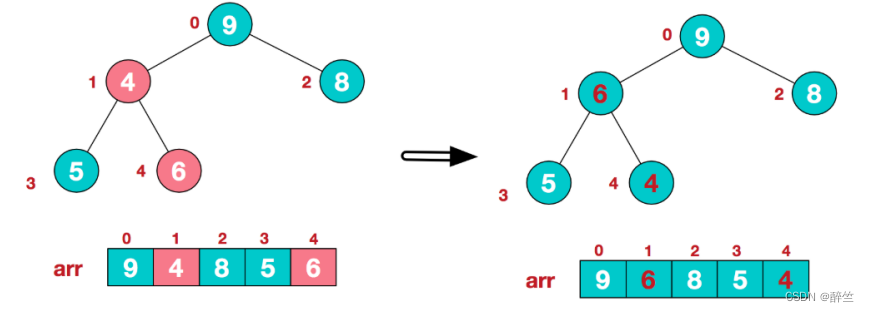
此时，我们就将一个无需序列构造成了一个大顶堆。

5、将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

将堆顶元素9和末尾元素4进行交换

重新调整结构，使其继续满足堆定义

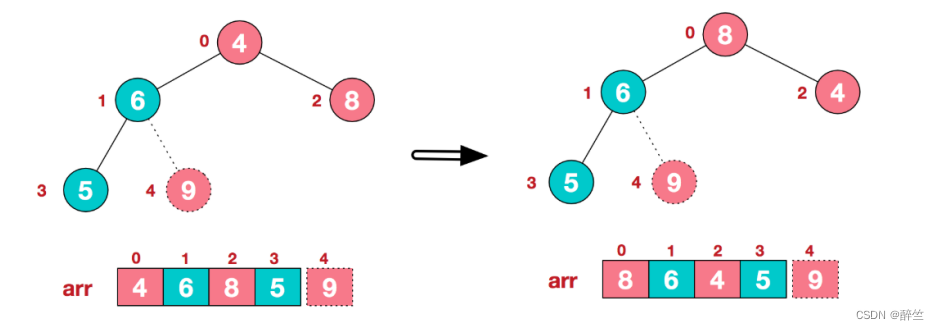
再将堆顶元素8与末尾元素5进行交换，得到第二大元素8

后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序，就可以得到从小到大的排好序的序列了。

代码实现：

void Swap(int* p1, int* p2) // 两节点元素交换位置
void AdjustDown(int* myarray, int length, int parent) // 堆节点向下调整(下沉)void HeapSort(int* myarray, int length)
{// 升序 -- 建大堆// 降序 -- 建小堆// 1.从第一个非叶子节点(分支节点)开始，往前进行向下调整建堆for (int i = (length / 2) - 1; i >= 0; i--) //时间复杂度：O(length)，推荐{AdjustDown(myarray, length, i);}//2.对堆节点进行调整排序//方法：第0个节点与最后一个节点交换、再从第0个节点开始往后进行向下调整int end = length - 1;while (end > 0){Swap(&myarray[0], &myarray[end]);AdjustDown(myarray, end, 0);end--;}
}// 两节点元素交换位置
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 堆的向下调整(下沉)
void AdjustDown(int* myarray, int length, int parent)
{int child = 2 * parent + 1; //先设左孩子节点较大while (child < length) //向下调整的终止条件为：双亲节点已经下沉到叶子节点位置，其child已大于数组的size越界{//选出左右孩子节点中较大的if (child + 1 < length && myarray[child + 1] > myarray[child]) //若右孩子节点存在且大于左孩子节点{child++; //设右孩子节点较大} //到这child为左右孩子中较大的节点if (myarray[child] > myarray[parent]){Swap(&myarray[parent], &myarray[child]);parent = child; //交换数据之后，可能就会影响到下一层了。所以还要继续向下调整child = 2 * parent + 1;}else{break;}}
}

到这，堆排序的实现就完成了，有什么疑问都可以在评论区或者私信我。如果你想学习更多有关堆的操作，例如堆的插入和删除，就看看这一篇文章吧《”堆“和二叉树顺序存储的”缘“》！

创作不易，如果您觉得本篇文章对您有一点帮助的话，希望您能点个赞支持我一下吧~⭐