图像变换类型

图像几何变换主要包括以下几种类型：

1. 平移（Translation）：将图像在水平或垂直方向上移动，不改变图像的尺寸和形状。
2. 缩放（Scaling）：改变图像的大小，可以是均匀缩放，即保持图像的长宽比，或者是非均匀缩放，即在水平和垂直方向上使用不同的缩放因子。
3. 旋转（Rotation）：将图像绕某一点（通常是图像中心）旋转一定角度，旋转后的图像位置会发生变化。
4. 镜像（Mirroring）：也称为翻转，可以是水平镜像或垂直镜像，即将图像沿水平轴或垂直轴翻转。
5. 仿射变换（AffineTransformation）：包括平移、缩放、旋转和错切等线性变换，保持直线和平行线的性质不变。
6. 透视变换（PerspectiveTransformation）：也称为投影变换，它涉及到三维空间中的点到二维平面的映射，可以模拟三维空间中物体的透视效果。

其中，又可以将其分为两大类：仿射变换和透视变换。透视变换的作用域是一个三维坐标系(x,y,z), 而仿射变换则是二维(x,y)平面变换。从另一个角度来说，仿射变换也可以看做是一种特殊的透视变换（z轴方向不变）。
透视变换和仿射变换的一个重要区别是：两条平行的线在经过仿射变换之后依然保持平行，但透视变换并不保证这一点。

仿射变换

为了统一将所有的仿射变换都用一种方式表达出来，引入了齐次坐标，这样就能够将平移变换和线性变换表示在一个矩阵中了。如下所示：

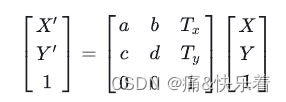
对于单个仿射变换，其矩阵表示如下：

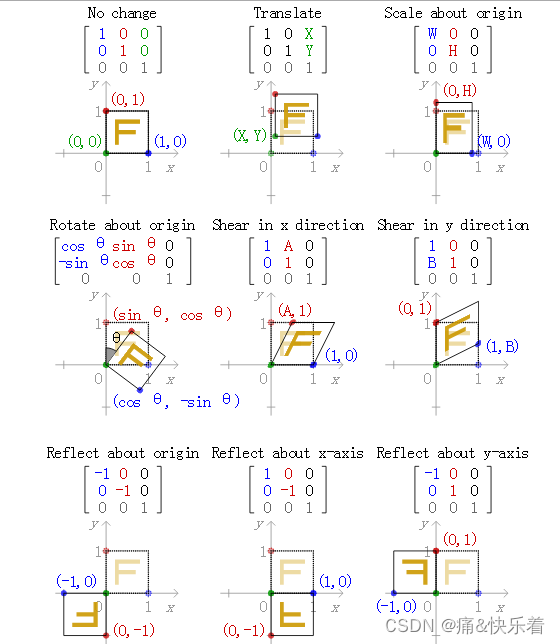
透视变换

透视变换（Perspective Transformation）是将二维的图片投影到一个三维视平面上，然后再转换到二维坐标下，所以也称为投影映射（Projective Mapping）。简单来说就是二维→三维→二维的一个过程。

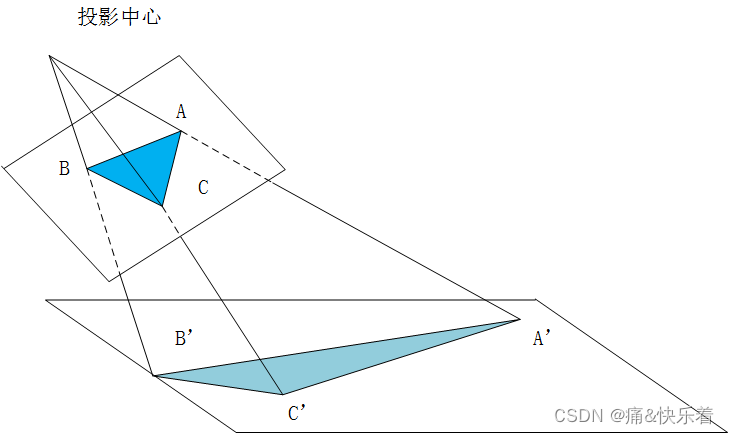
透视变换的矩阵表示如下，我们可以看到它与仿射变换的区别便是最后一行的参数c1和c2的值，对于仿射变换c1=c2=0。


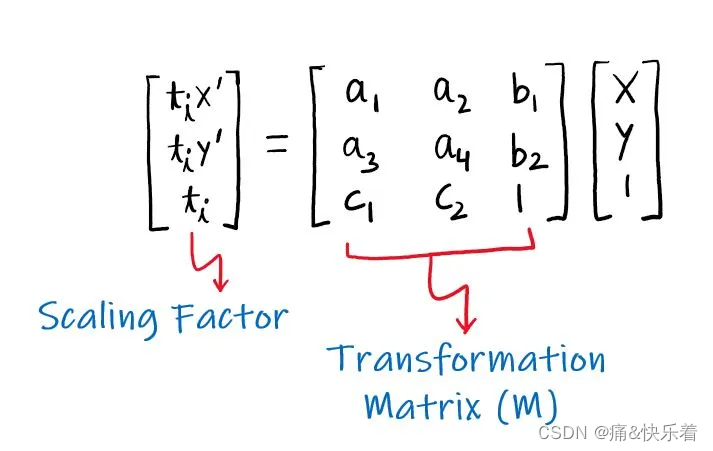
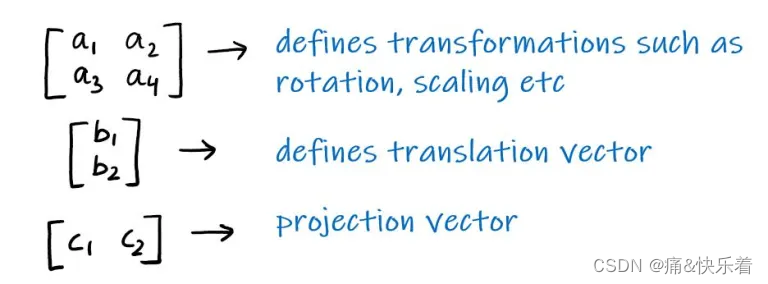
通过透视变换的变换矩阵计算新的坐标，其中a33=1，x’和y’为最终计算的结果。



至此，已经知道了仿射变换和透视变换的变换矩阵，那在实际应用时该如何求呢？一个方法是直接根据几何参数计算变换矩阵，另外一个方法是通过原始图像坐标和目标图像坐标求解变换矩阵。通常情况下，更多选择是后者的计算方法。

对于仿射变换，只有6个参数，因此只需要3个点对就可以求解了；而透视变换，则需要8个参数，需要4个点对才能够求解。如下所示为透视变换矩阵的8个方程组。

python-opencv实现

图像几何变换在计算机视觉和图像处理中有着广泛的应用，如图像配准、目标识别、图像校正等。在实际应用中，这些变换通常通过变换矩阵来实现，可以通过OpenCV等图像处理库来进行操作。

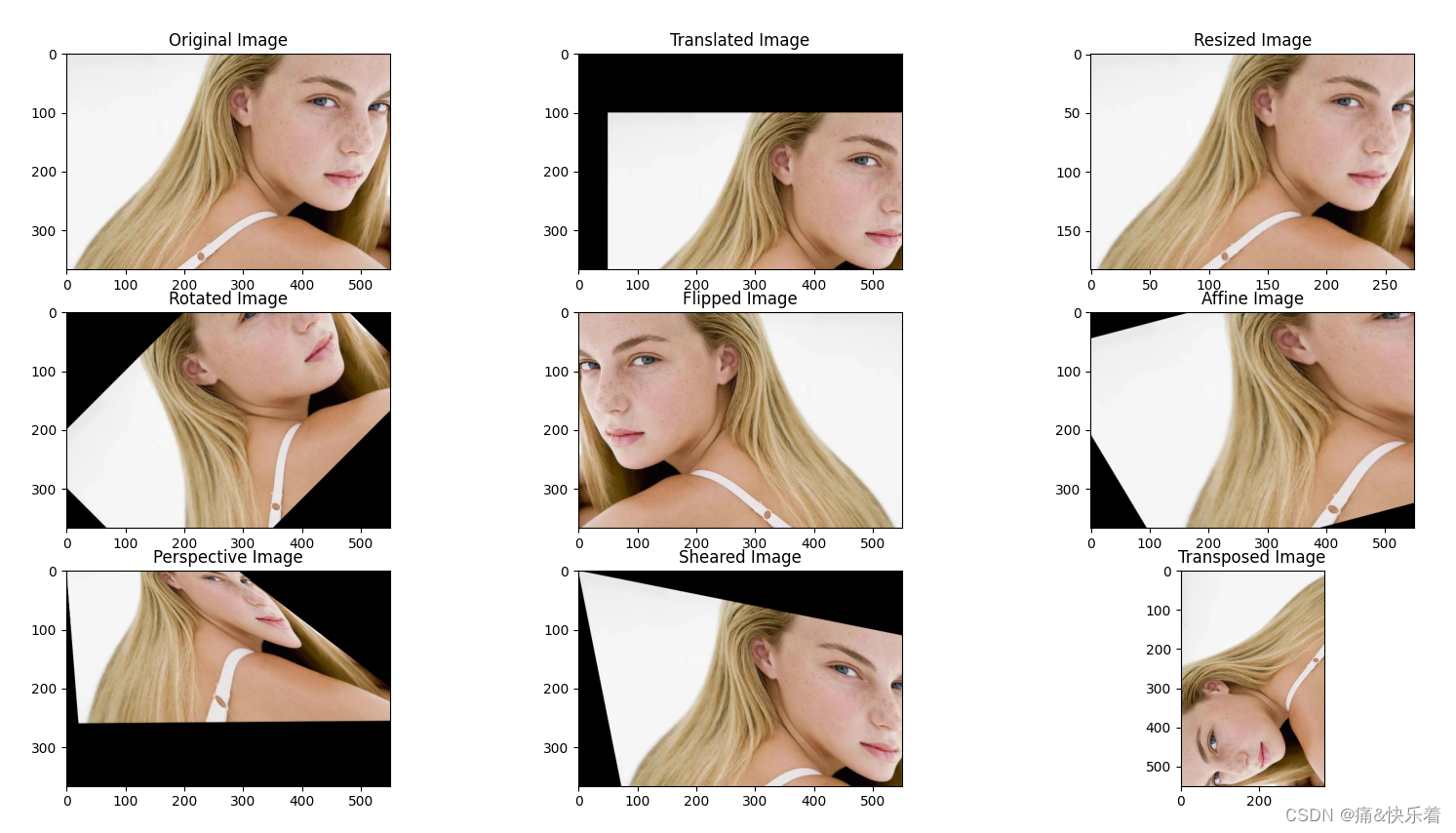
这是用chatgpt写的代码：

import cv2
import numpy as np
import matplotlib.pyplot as plt# 读取图像
image = cv2.imread('../images/girl1.jpg')# 平移变换
rows, cols = image.shape[:2]
M_translation = np.float32([[1, 0, 50], [0, 1, 100]])  # 水平移动50像素，垂直移动100像素
translated_image = cv2.warpAffine(image, M_translation, (cols, rows))# 缩放变换
scale_factor = 0.5  # 缩小为原来的一半
resized_image = cv2.resize(image, None, fx=scale_factor, fy=scale_factor)# 旋转变换
center = (cols // 2, rows // 2)
angle = 45  # 旋转角度为45度
M_rotation = cv2.getRotationMatrix2D(center, angle, 1)
rotated_image = cv2.warpAffine(image, M_rotation, (cols, rows))# 镜像变换（水平镜像）
flipped_image = cv2.flip(image, 1)  # 参数1表示水平镜像，参数0表示垂直镜像# 仿射变换
pts1 = np.float32([[50, 50], [200, 50], [50, 200]])
pts2 = np.float32([[10, 100], [200, 50], [100, 250]])
M_affine = cv2.getAffineTransform(pts1, pts2)
affined_image = cv2.warpAffine(image, M_affine, (cols, rows))# 透视变换
pts3 = np.float32([[0, 65], [368, 52], [28, 387], [389, 390]])
pts4 = np.float32([[0, 0], [200, 0], [60, 300], [500, 300]])
M_perspective = cv2.getPerspectiveTransform(pts3, pts4)
perspective_image = cv2.warpPerspective(image, M_perspective, (cols, rows))# 错切变换
M_shearing = np.float32([[1, 0.2, 0], [0.2, 1, 0]])
sheared_image = cv2.warpAffine(image, M_shearing, (cols, rows))# 转置变换
transposed_image = cv2.transpose(image)# 显示结果图像
plt.figure()
plt.subplot(331)
plt.imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
plt.title('Original Image')plt.subplot(332)
plt.imshow(cv2.cvtColor(translated_image, cv2.COLOR_BGR2RGB))
plt.title('Translated Image')plt.subplot(333)
plt.imshow(cv2.cvtColor(resized_image, cv2.COLOR_BGR2RGB))
plt.title('Resized Image')plt.subplot(334)
plt.imshow(cv2.cvtColor(rotated_image, cv2.COLOR_BGR2RGB))
plt.title('Rotated Image')plt.subplot(335)
plt.imshow(cv2.cvtColor(flipped_image, cv2.COLOR_BGR2RGB))
plt.title('Flipped Image')plt.subplot(336)
plt.imshow(cv2.cvtColor(affined_image, cv2.COLOR_BGR2RGB))
plt.title('Affine Image')plt.subplot(337)
plt.imshow(cv2.cvtColor(perspective_image, cv2.COLOR_BGR2RGB))
plt.title('Perspective Image')plt.subplot(338)
plt.imshow(cv2.cvtColor(sheared_image, cv2.COLOR_BGR2RGB))
plt.title('Sheared Image')plt.subplot(339)
plt.imshow(cv2.cvtColor(transposed_image, cv2.COLOR_BGR2RGB))
plt.title('Transposed Image')plt.show()

参考文献

[1] 仿射变换（Affine Transformation）在2D和3D坐标下的变换矩阵
[2] (十四）透视变换
[3] 算法笔记 : 透视变换(透射变换)
[4] 仿射变换和透视变换矩阵的参数含义与区别