---

1.背景

2016年，Mirjalili 等人受到宇宙膨胀理论启发，提出了多元宇宙优化算法(Multi-verse Optimization, MVO)。

2.算法原理

2.1算法思想

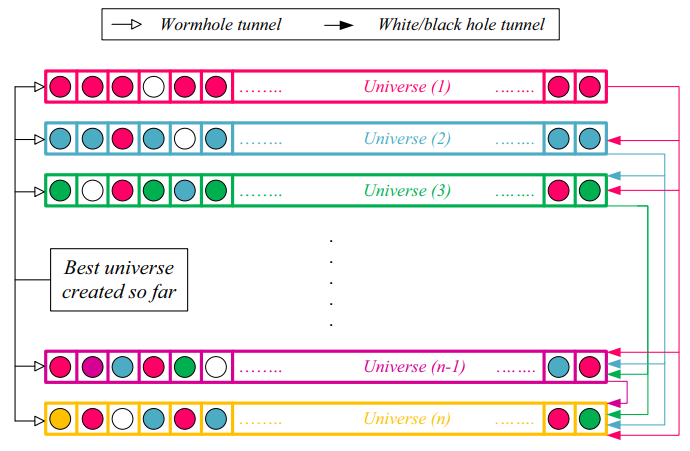
MVO基于宇宙膨胀的原理，利用白洞和黑洞的不同膨胀率，模拟了宇宙中粒子通过虫洞从白洞向黑洞位置转移的过程。MVO有以下规则：

• 膨胀率越高，产生白洞的概率越高
• 膨胀率越高，产生黑洞的概率越低
• 膨胀率较高的宇宙倾向于通过白洞发送物体。
• 膨胀率较低的宇宙倾向于通过黑洞接收更多物体
• 所有宇宙中的物体可能通过虫洞朝着最佳宇宙进行随机移动，而不受膨胀率的影响

2.2算法过程

多元宇宙：
每一行可以看作一个宇宙，行向量上每一维看作黑洞。
$$U=\left[\begin{array}{cccc}{x}_1^1& x_1^2& \dots & x_1^d\\ x_2^1& x_2^2& \dots & x_2^d\\ ⋮& ⋮& ⋮& ⋮\\ x_n^1& x_n^2& \dots & x_n^d\end{array}\right]$$
$$x_i^j=\{\begin{array}{cc}{x}_k^j& r1<NI(Ui)\\ x_i^j& r1\ge NI(Ui)\end{array}$$
其中，NI为宇宙膨胀率。

黑洞位置更新：
$$x_i^j=\{\begin{array}{l}\{\begin{array}{ll}{X}_j+\mathrm{TDR}\times \left(\left(u{b}_j-l{b}_j\right)\times r4+l{b}_j\right)& r3<0.5\\ X_j-\mathrm{TDR}\times \left(\left(u{b}_j-l{b}_j\right)\times r4+l{b}_j\right)& r3\ge 0.5\\ x_i^j& r2\ge \mathrm{WEP}\end{array}\end{array}$$
其中，TDR为旅行距离率：
$$\mathrm{TDR}=1-\frac{l^{1/p}}{L^{1/p}}$$
虫洞存在率：
$$\mathrm{WEP}=\min +l\times \left(\frac{\max -\min }{L}\right)$$

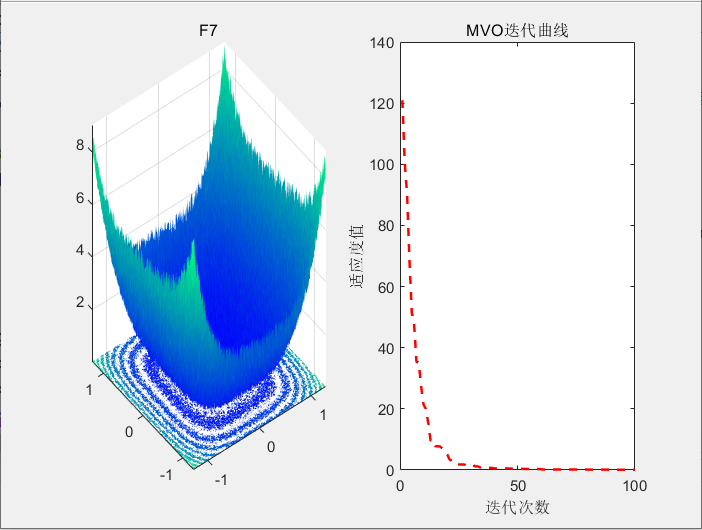
3.结果展示

4.参考文献

[1] Mirjalili S, Mirjalili S M, Hatamlou A. Multi-verse optimizer: a nature-inspired algorithm for global optimization[J]. Neural Computing and Applications, 2016, 27: 495-513.