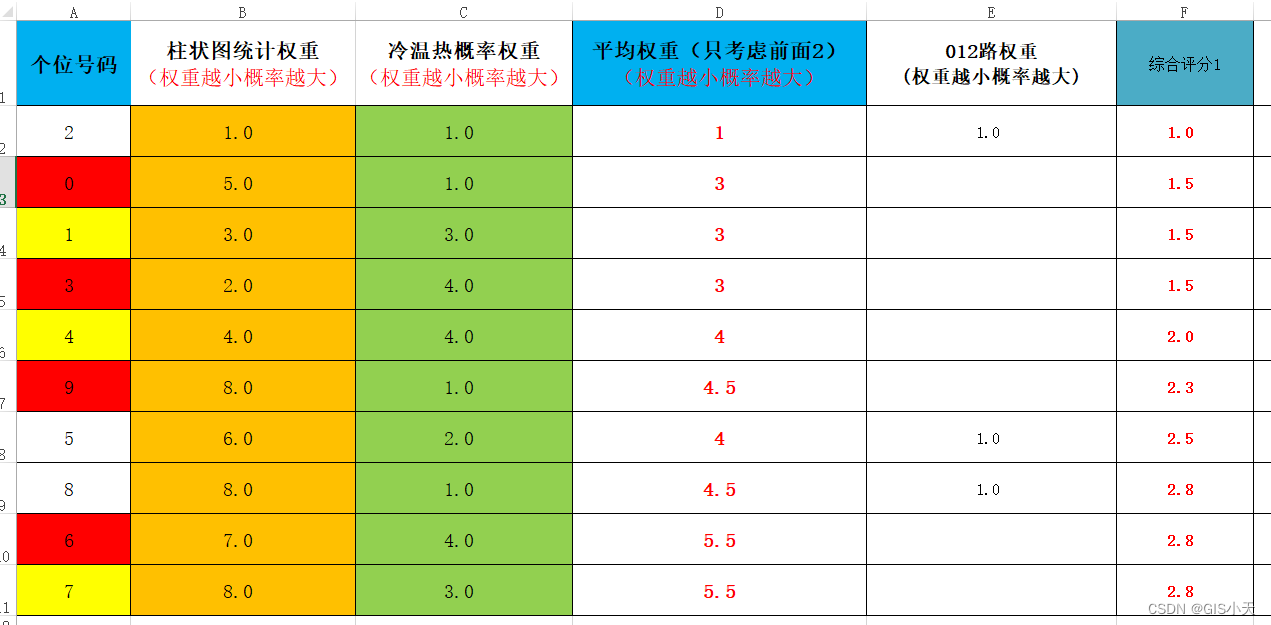
这题用递归暴力的方法如下：

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int num;
int N,M;
void dfs(int now,int n,int m)
{if(now<=0 || n>N ||m>M)return ;if(n==N && m==M){if(now==1)num+=1;return;}dfs(now-1,n,m+1);dfs(now*2,n+1,m);return ;
}
int main()
{cin>>N>>M;M=M-1;num=0;dfs(2,0,0);cout<<num<<endl;return 0;
}

但是很显然这个方法耗的时间很长，只能通过部分示例。那么我们要另寻他法。

动态规划是一个好方法，但是实际操作过程中还是不那么好想。
 

思路分析：

1. 我们使用动态规划来解决这个问题。我们使用一个三维数组 dp[i][j][k] 来表示到了i次店，j次看花后剩余k斗酒的方案数。
2. 初始状态是在0次到达0位置时，剩余2斗酒的方案数为1。
3. 我们从i=0到N，j=0到M，k=0到M进行遍历，填充动态规划数组dp。
4. 在填表的过程中，我们根据题目描述的店和花的情况来更新状态，其中i表示到达店的次数，j表示遇到花的次数，k表示剩余的酒量。
5. 最终，我们输出dp[N][M-1][1]，表示在N次到达M-1位置时，剩余1斗酒的方案数。

#include<iostream>
#include<vector>
using namespace std;int main() {// 读取输入的N和Mint N, M;cin >> N >> M;// 初始化动态规划数组dp，dp[i][j][k]表示到了i次店，j次看花后剩余k斗酒的方案数vector<vector<vector<long long>>> dp(N + 1, vector<vector<long long>>(M + 1, vector<long long>(M + 1, 0)));// 初始状态：在0次到店和0次看花后，剩余2斗酒的方案数为1dp[0][0][2] = 1;// 开始动态规划，逐步填表for (int i = 0; i <= N; i++) {for (int j = 0; j <= M; j++) {// 当i和j均为0时，表示初始状态，跳过if (i == 0 && j == 0) continue;// 遍历剩余酒量kfor (int k = 0; k <= M; k++) {// 如果k是偶数且i大于0，表示从上一次到店有剩余酒量为k的情况下，下一次到店的方案数if (k % 2 == 0 && i > 0)dp[i][j][k] += dp[i - 1][j][k / 2];// 如果j大于0，表示从上一次到店有剩余酒量为k的情况下，下一次看花的方案数if (j > 0)dp[i][j][k] += dp[i][j - 1][k + 1];// 对结果取模dp[i][j][k] %= 1000000007;}}}// 输出结果：在N次到店和M-1次看花后，剩余1斗酒的方案数cout << dp[N][M - 1][1] << endl;return 0;
}