目录

1 主要内容

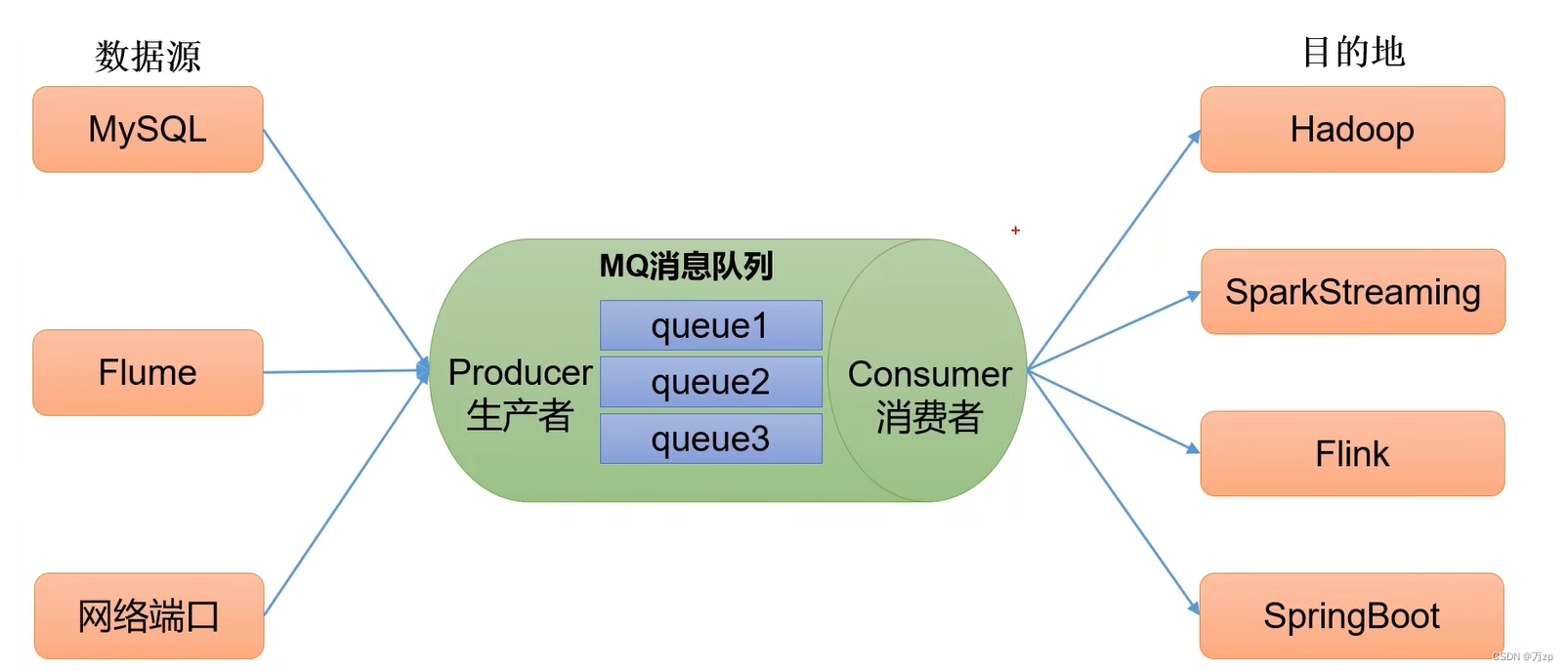
模型示意图

电能交易流程

模型亮点

2 部分代码

3 程序结果

4 下载链接

---

1 主要内容

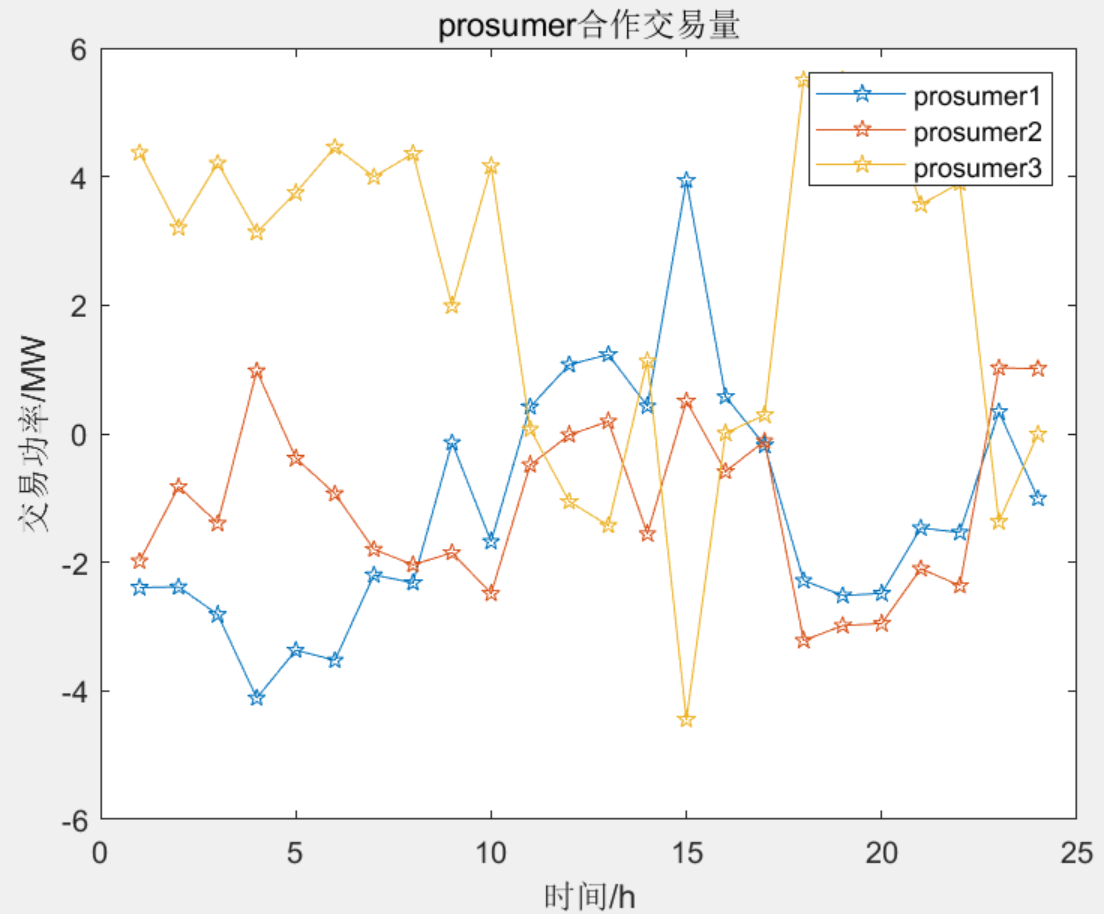
程序复现文章《A cooperative Stackelberg game based energy management considering price discrimination and risk assessment》，建立基于主从博弈的考虑差别定价和风险管理的微网动态定价与调度策略模型，构建了双层能源管理框架，上层为零售商的动态定价模型，目标是社会福利最大化；下层是多个产消者的合作博弈模型，优化各产消者的能量管理策略，各产消者之间可以进行P2P交易。同时，采用纳什谈判法对多个产消者的合作剩余进行公平分配，还考虑了运行风险，采用条件风险价值（CVaR）随机规划方法来描述零售商的预期损失。

• 模型示意图

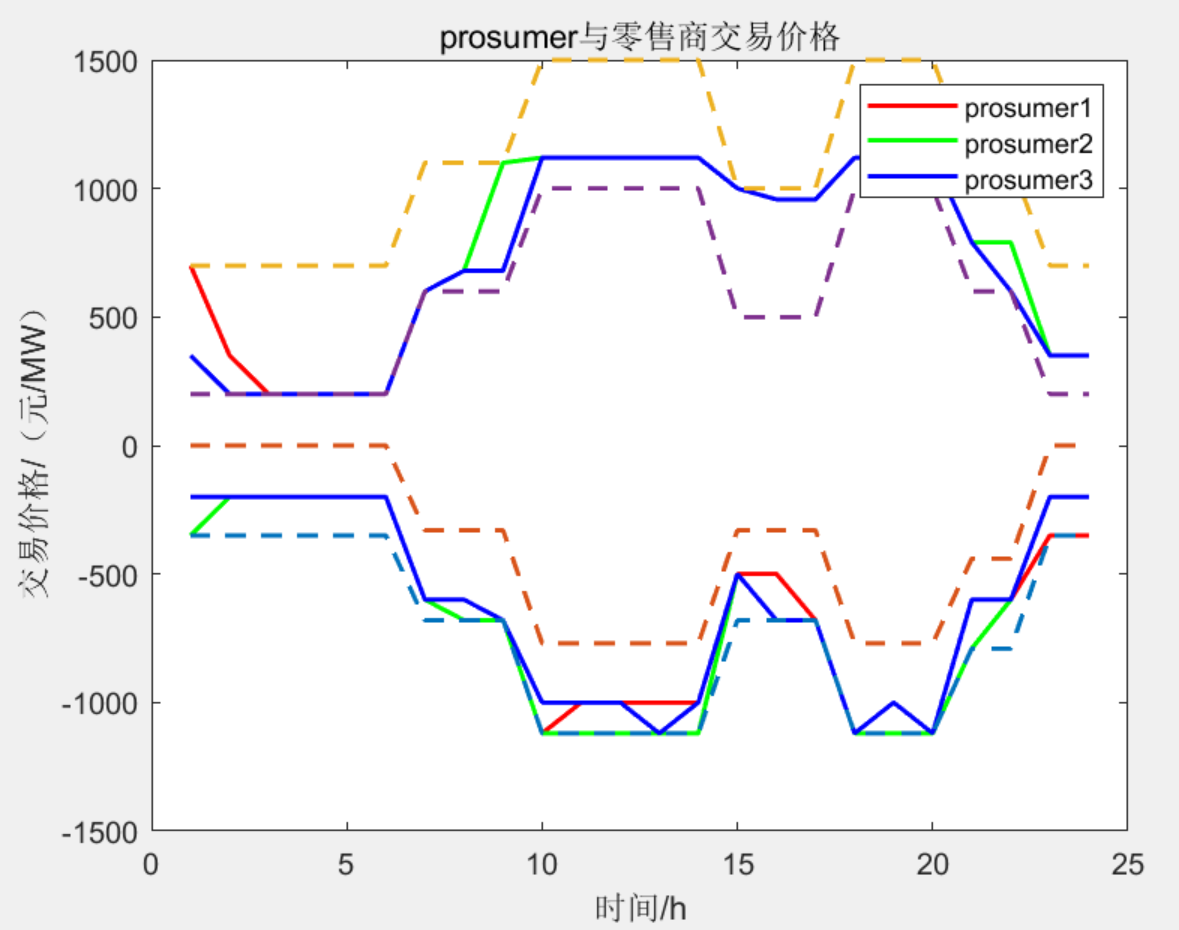
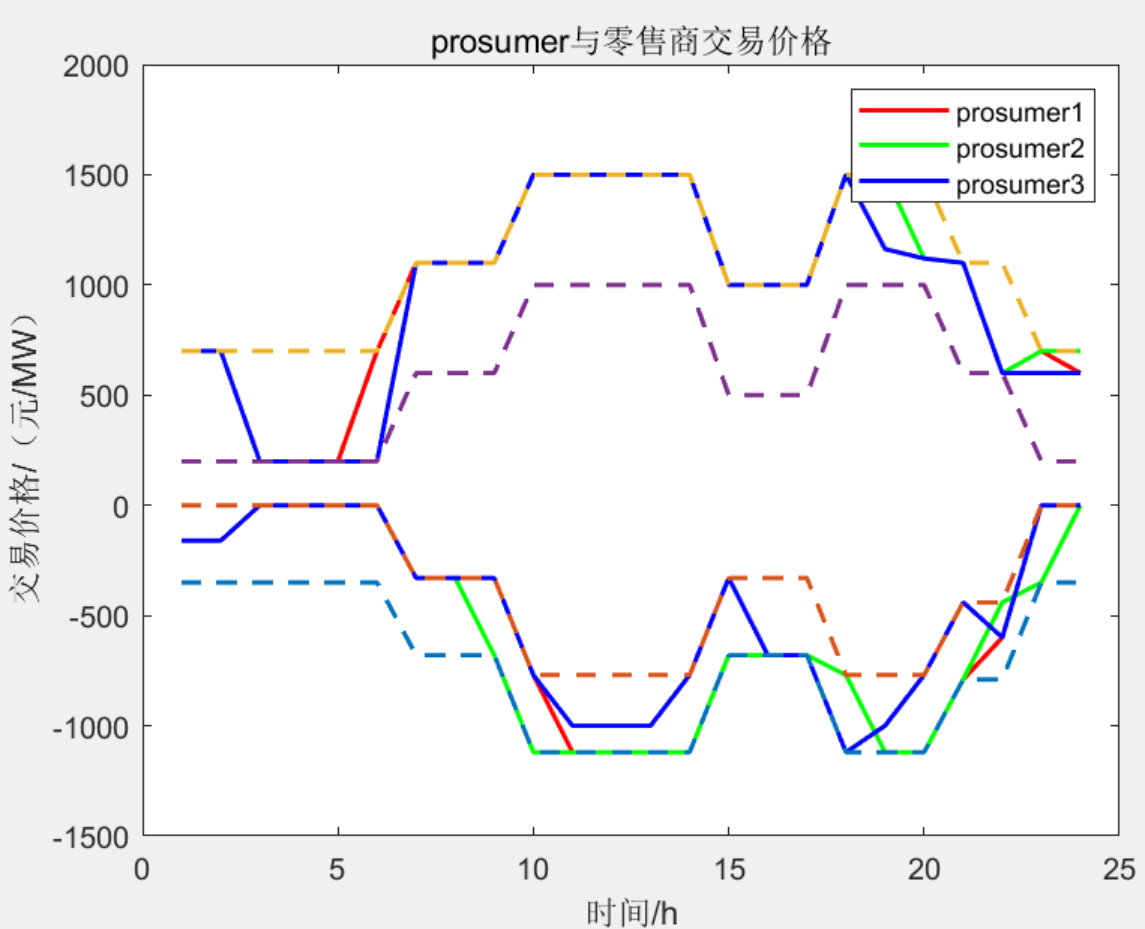
• 电能交易流程

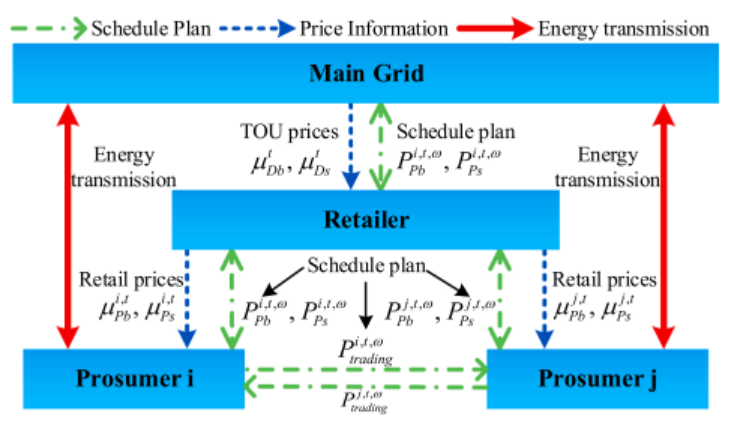
• 模型亮点

该模型通过建立双层模型，出现了双线性和非线性问题，为了解决该问题，引入 kkt条件和大M法将原模型转化为等效单层模型，从而进行求解。而且程序采用三种对比算例进行分析，非常方便对照学习，算例1和2采用matlab+cplex求解，算例3采用matlab+mosek求解！

2 部分代码

%% 模型参数设定
%产消者/零售商从主网购电价格 元/MW
u_Db=1e3*[0.4,0.4,0.4,0.4,0.4,0.4,0.79,0.79,0.79,1.2,1.2,1.2,1.2,1.2,0.79,0.79,0.79,1.2,1.2,1.2,0.79,0.79,0.4,0.4];
%产消者/零售商向主网售电价格 元/MW
u_Ds=1e3*[0.35,0.35,0.35,0.35,0.35,0.35,0.68,0.68,0.68,1.12,1.12,1.12,1.12,1.12,0.68,0.68,0.68,1.12,1.12,1.12,0.79,0.79,0.35,0.35];
%零售商与产消者的交易价格上下限
u_Pbmax=1e3*[0.7,0.7,0.7,0.7,0.7,0.7,1.1,1.1,1.1,1.5,1.5,1.5,1.5,1.5,1,1,1,1.5,1.5,1.5,1.1,1.1,0.7,0.7];%购价上限
u_Pbmin=u_Pbmax-0.5*1e3*ones(1,24);%购价下限
u_Psmax=u_Ds;%售价上限
u_Psmin=u_Psmax-0.35*1e3*ones(1,24);%售价下限
%产消者1-3  电负荷 MW
P_load_1=[6.62295082,5.770491803,5.442622951,5.31147541,5.37704918,5.573770492,6.295081967,6.491803279,7.213114754,7.803278689,8.131147541,8.131147541,7.93442623,7.278688525,7.016393443,7.016393443,7.147540984,8.262295082,9.442622951,9.37704918,9.37704918,7.93442623,6.819672131,5.901639344];
P_load_2=[3.344262295,3.016393443,2.754098361,2.754098361,2.754098361,2.885245902,3.147540984,3.344262295,3.639344262,3.93442623,4,4.131147541,4,3.737704918,3.475409836,3.606557377,3.606557377,4.131147541,4.721311475,4.655737705,4.721311475,4,3.409836066,3.016393443];
P_load_3=[11.60655738,10.16393443,9.442622951,9.245901639,9.114754098,9.639344262,10.75409836,11.3442623,12.45901639,13.50819672,14.10772834,14.16393443,13.63934426,12.72131148,12.19672131,12.32786885,12.59016393,14.29508197,16.59016393,16.45901639,16.26229508,13.7704918,12.13114754,10.55737705];
%产消者1-3  导入10个场景的出力和概率
Sw=10; %场景数量
load P_Gen.mat  %产消者1风电出力    P_Gen_1  维度：10*24     P_Gen_2    P_Gen_3 
%产消者1-3风电场景概率
pai_1=0.1*ones(1,10);pai_2=0.1*ones(1,10);pai_3=0.1*ones(1,10);
%其它固定参数
C_E=80; %储能充放成本
P_Pbmax=15; %最大购电量
P_Psmax=15; %最大售电量
Cap=10; %最大储能容量MW
P_Ecmax=3; %充放能功率上限
P_Edmax=3; %充放能功率上限
SOCmin=0.2; %最小存储量百分比 单位%
SOCmax=0.85; %最大容量百分比
SOCini=0.33; %初始容量百分比
SOCexp=0.85; %末段容量百分比
M=1E8; %大M法
beta=0.1; %厌恶风险系数
%% 决策变量初始化
delta=sdpvar(1,3);
eta_1=sdpvar(Sw,1); %产消者1的风险调度辅助变量
eta_2=sdpvar(Sw,1); %产消者2的风险调度辅助变量
eta_3=sdpvar(Sw,1); %产消者3的风险调度辅助变量
P_Ps_1=sdpvar(Sw,24); %零售商向产消者1售能量
P_Ps_2=sdpvar(Sw,24); %零售商向产消者2售能量
P_Ps_3=sdpvar(Sw,24); %零售商向产消者3售能量
P_Pb_1=sdpvar(Sw,24); %零售商从产消者1购能量
P_Pb_2=sdpvar(Sw,24); %零售商从产消者2购能量
P_Pb_3=sdpvar(Sw,24); %零售商从产消者3购能量
u_Ps=sdpvar(3,24); %零售商向产消者购能价格
u_Pb=sdpvar(3,24); %零售商从产消者购能价格
P_trading_1=sdpvar(Sw,24); %产消者1合作博弈交易量
P_trading_2=sdpvar(Sw,24); %产消者2合作博弈交易量
P_trading_3=sdpvar(Sw,24); %产消者3合作博弈交易量
SOC_1=sdpvar(Sw,24); %产消者1储能容量状态 单位%
SOC_2=sdpvar(Sw,24); %产消者2储能容量状态 单位%
SOC_3=sdpvar(Sw,24); %产消者3储能容量状态 单位%
P_Ec_1=sdpvar(Sw,24); %储能充电
P_Ec_2=sdpvar(Sw,24); %储能充电
P_Ec_3=sdpvar(Sw,24); %储能充电
P_Ed_1=sdpvar(Sw,24); %储能放电
P_Ed_2=sdpvar(Sw,24); %储能放电
P_Ed_3=sdpvar(Sw,24); %储能放电
Uabs_1=binvar(Sw,24); %储能充放电状态，0-1变量
Uabs_2=binvar(Sw,24); %储能充放电状态，0-1变量
Uabs_3=binvar(Sw,24); %储能充放电状态，0-1变量
Urelea_1=binvar(Sw,24); %储能充放电状态，0-1变量
Urelea_2=binvar(Sw,24); %储能充放电状态，0-1变量
Urelea_3=binvar(Sw,24); %储能充放电状态，0-1变量
%定义KKT条件中的拉格朗日乘子

3 程序结果

4 下载链接