transformer的学习：Attention is all you need

整体概述：编辑编辑

encoder：

embedding：

编辑

self-attention：

向量的相似度计算：

qkv怎么来的编辑

softmax：

code

multi-head-attention

位置编码：

残差&&FFN：

decoder：

cross-attention

self-attention

Linear + softmax

Train&&loss

ref:

找到了一篇写的很好的贴子，记录一些学习笔记：

https://jalammar.github.io/illustrated-transformer/

注意力机制（Attention），这是现代深度学习模型中常见的一种方法。注意力机制在神经机器翻译应用中起到了提升性能的作用。本文将介绍Transformer模型，它利用注意力机制提高了模型的训练速度。在某些任务中，Transformer模型的性能超过了Google神经机器翻译模型。然而，最大的好处来自于Transformer模型在并行化方面的优势。实际上，Google Cloud建议使用Transformer模型作为参考模型来使用他们的Cloud TPU服务。

Transformer模型是在论文《Attention is All You Need》中提出的。TensorFlow的一个实现可以在Tensor2Tensor软件包中找到。哈佛大学的自然语言处理研究组创建了一个带有PyTorch实现的指南。

整体概述：

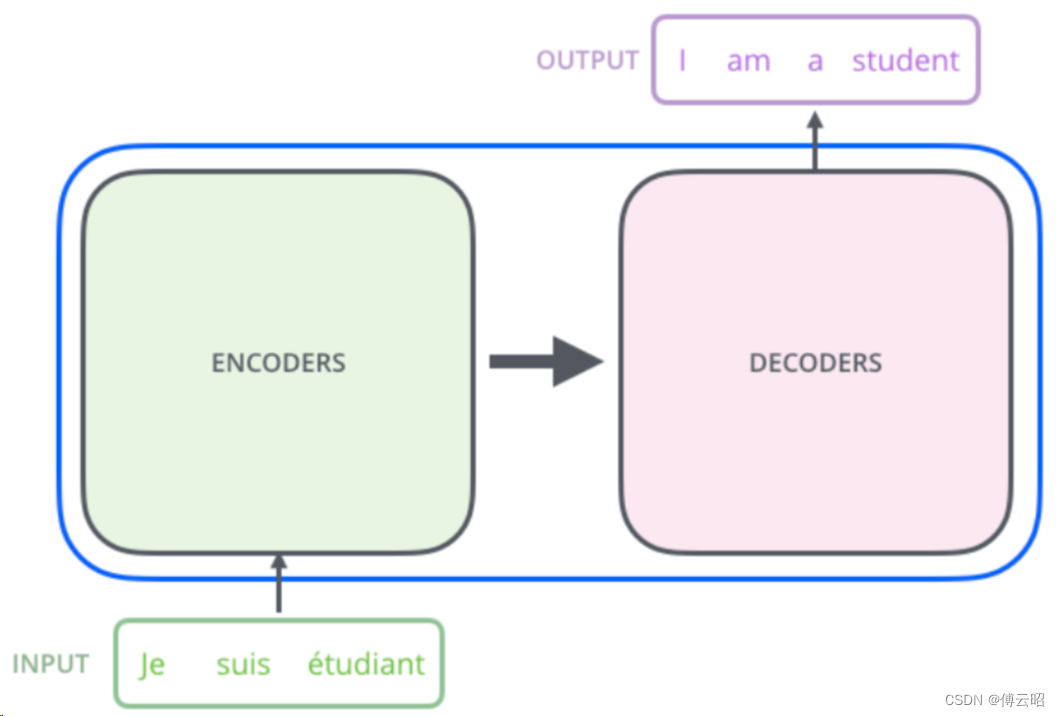
Transformers = encoders + decoders

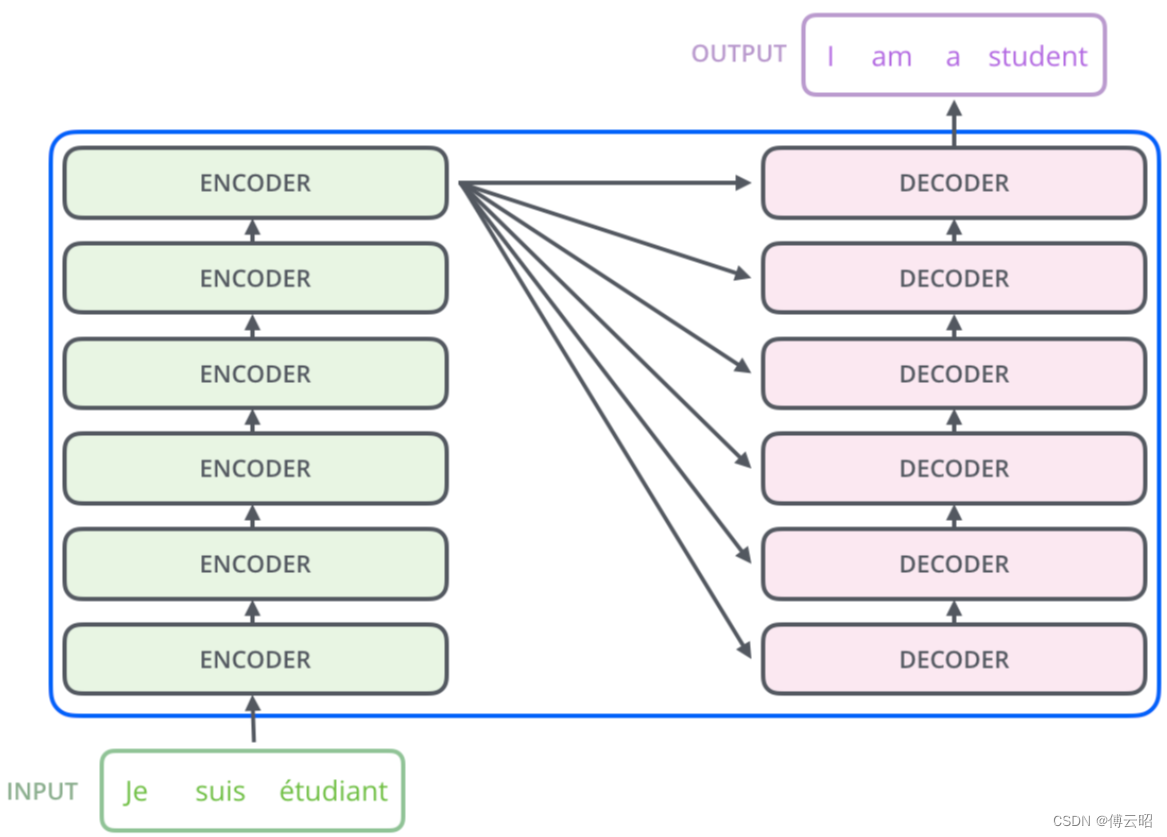
Encoders = 6 * encoder

Decoders = 6 * decoder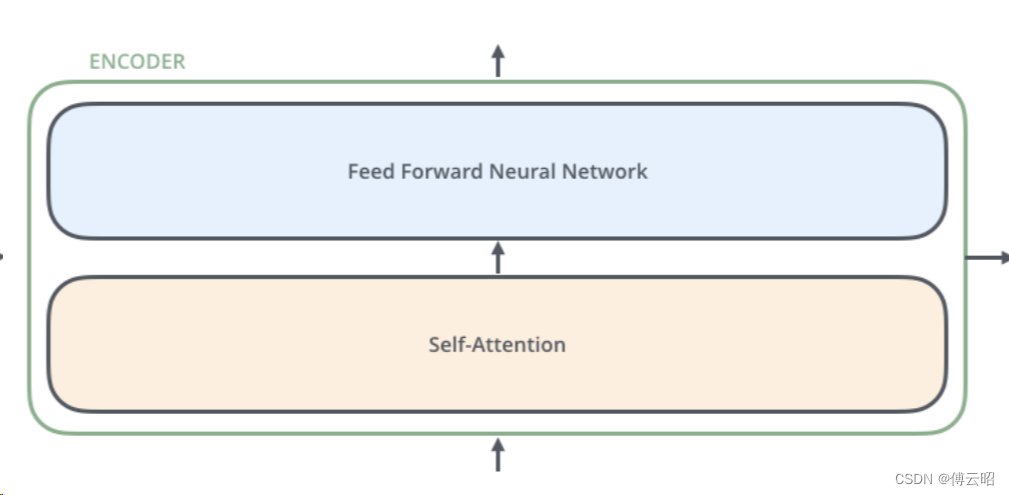

Encoder = self-attention + feed forward nn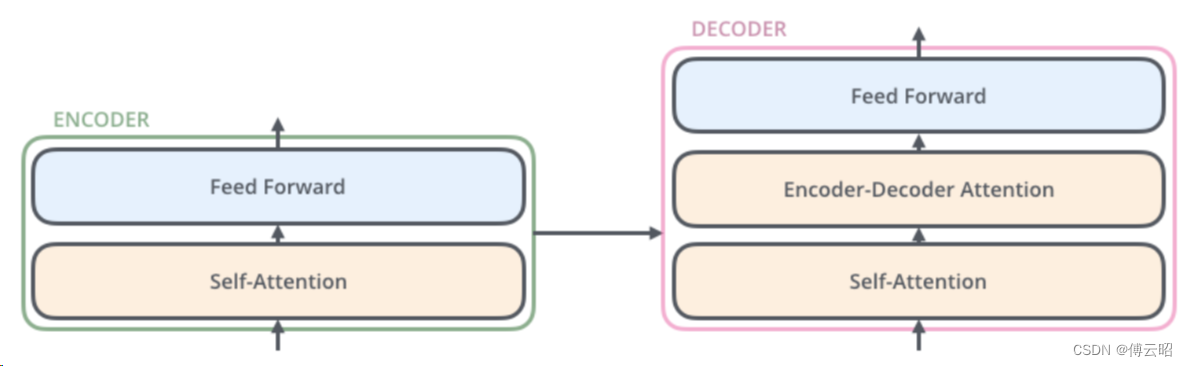

Decoder = self-attention + encoder-decoder attention(cross attention) + Feed Forward

encoder-decoder attention：q来自decoder，k和v来自encoder

encoder：

embedding：

文本-->数字，计算机只认识数字

在Transformer模型中，输入序列的词嵌入（word embedding）是模型的一部分，用于将离散的词或标记映射到连续的向量表示。Transformer中的词嵌入被称为输入嵌入（input embedding）。

输入嵌入的作用是将输入序列中的每个词或标记转换为连续的低维向量表示，以便模型能够对其进行处理。这些嵌入向量可以捕捉词语之间的语义和语法信息，从而提供有关词语的上下文表示。

通常情况下，输入嵌入是通过一个可训练的矩阵（通常称为嵌入矩阵）来实现的。该矩阵的大小为词汇表的大小（词汇表中唯一词汇的数量）乘以词嵌入的维度。在训练过程中，嵌入矩阵的参数会随着模型的训练而学习得到。

在Transformer中，输入嵌入通常与位置编码进行相加，以融合词汇和位置信息。这样，每个输入位置都具有一个综合的表示，其中包括词汇信息和相对位置信息。

需要注意的是，Transformer模型中的嵌入层可以是单独的一层，也可以与其他层（如位置编码层、注意力层、前馈神经网络层）一起构成一个整体的模型。输入嵌入在Transformer中起到了将离散的输入序列转换为连续的向量表示的重要作用，为模型提供了有效的输入表示。

torch.nn.embedding()实现

self-attention：

计算相似度。把文本embedding为一个个的词向量token，然后直接相乘（投影）来计算相似度。

上面可以看出it和the animal的相似度很高，以为it就是代指the animal，和because的相似度很低，没啥关系，一个是关系代词，一个是因果连词。

在Transformer模型中，自注意力机制（self-attention）是其核心组成部分之一，也被称为注意力机制（attention mechanism）。自注意力机制允许模型在处理输入序列时，根据序列中不同位置的相关性动态地分配注意力权重。

自注意力机制的目的是对输入序列中的每个位置进行编码，并建立位置之间的关联。它通过计算一个注意力分数来确定每个位置与其他位置之间的关联强度，然后利用这些关联强度对位置的表示进行加权求和。

在Transformer中，自注意力机制的计算过程分为三个步骤：查询（query）、键（key）和值（value）。

查询（Query）：对于每个位置，通过一个线性变换将输入序列中的每个位置映射到一个查询向量，表示该位置的特征。
键（Key）和值（Value）：同样，通过线性变换将输入序列中的每个位置映射到键向量和值向量。键向量用于计算注意力权重，值向量用于加权求和。
注意力计算：利用查询向量、键向量和值向量计算注意力权重。注意力权重表示每个位置与其他位置之间的关联强度。一般使用点积注意力或加性注意力机制来计算注意力权重。
1. 点积注意力：通过计算查询向量和键向量之间的点积，然后进行标准化处理，得到注意力权重。
2. 加性注意力：通过将查询向量和键向量进行线性变换后相加，并应用激活函数，然后进行标准化处理，得到注意力权重。
加权求和：利用注意力权重对值向量进行加权求和，得到每个位置经过注意力机制后的表示。

自注意力机制可以将输入序列中的不同位置之间的相关性进行建模，从而使模型能够根据输入的上下文动态地分配注意力。这种机制使得Transformer能够在处理序列任务时更好地捕捉长距离依赖关系，提高模型的性能和泛化能力。注意力机制被广泛应用于自然语言处理和机器翻译等任务中。

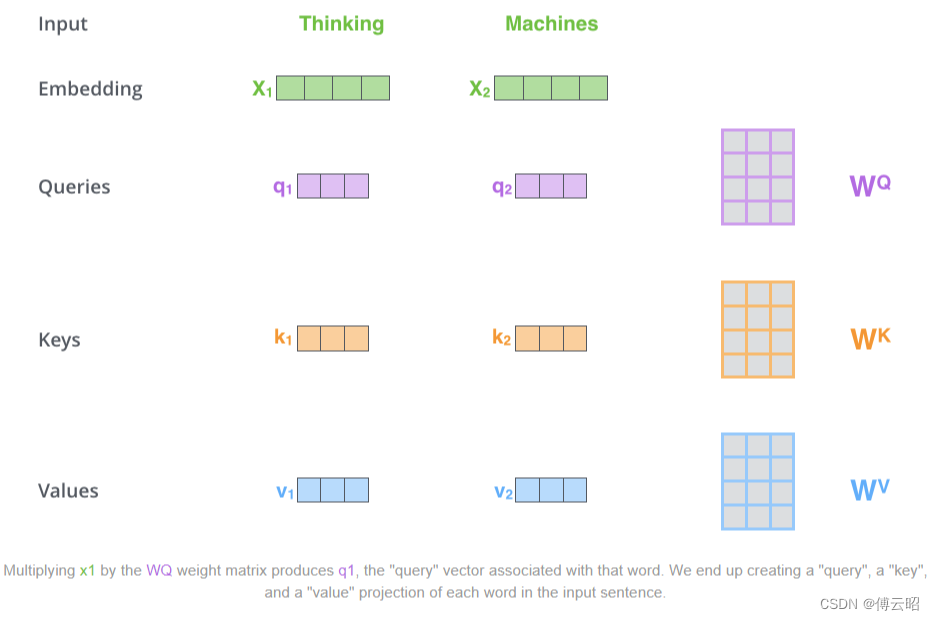
x-->q,k,v 使用fc，把维度从embedding后的x的512 mapping到64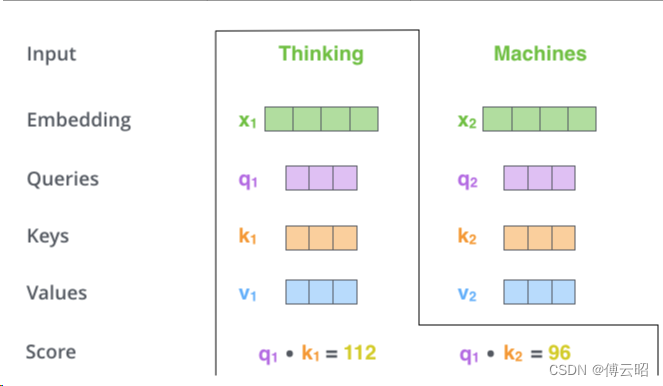

key：可以看作一本书的目录

value：某一章节（key）里面的内容

query：你的查询关键词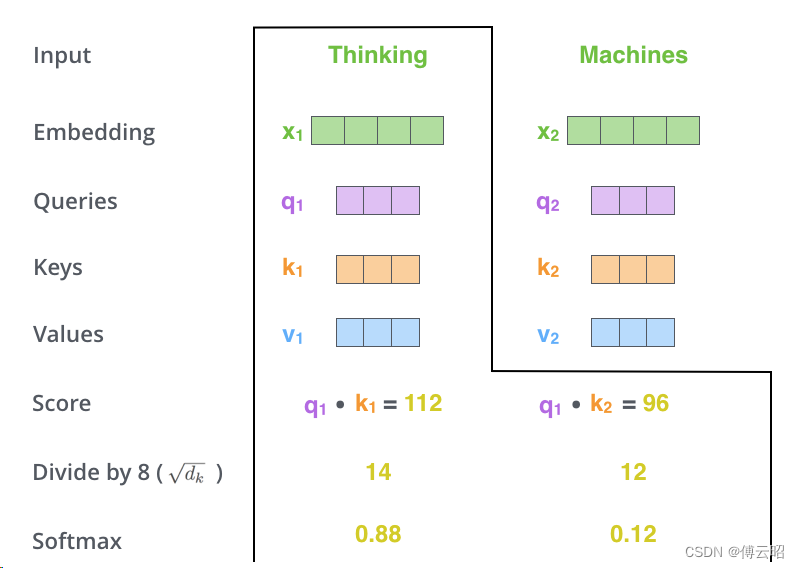

除以8（论文中使用的键向量维度的平方根 - 64）。这样做可以使梯度更加稳定。将结果通过softmax操作进行处理。Softmax函数对得分进行归一化，使得它们都为正值且总和为1。

softmax后的值表示的是相似度权重weight的意思，即最后的权重分配中，k1分的权重是0.88，k2只有0.12，表达的意思是k1和q1更加相似，所以权重更大。

比如：q1是猫a，k1是猫b，k2是狗，那么猫a和猫b的相似度>猫a和狗的相似度，所以猫b的权重是0.88，狗的权重是0.12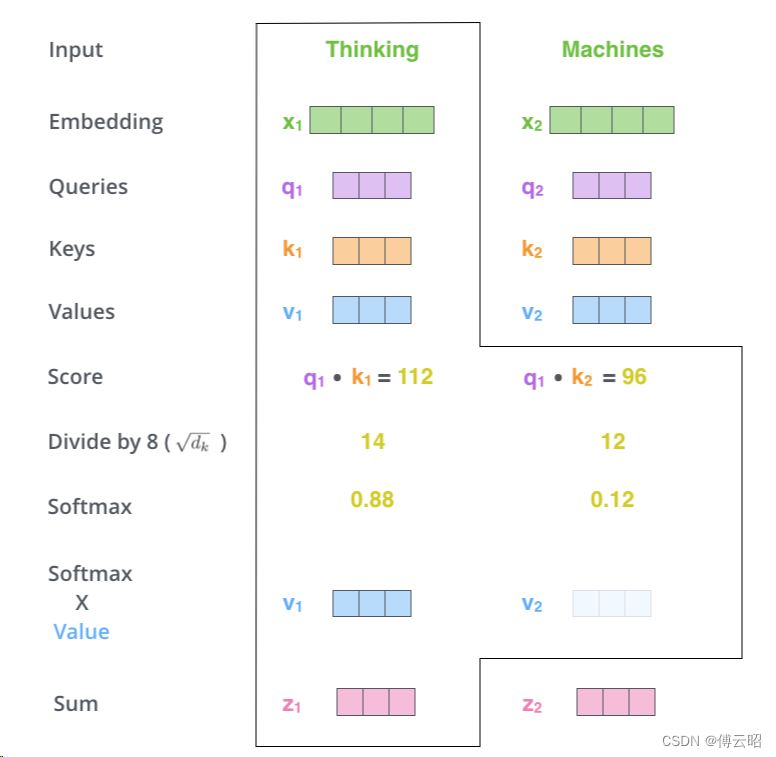

Z = sum(权重 * value)

向量的相似度计算：

Cos (θ) = (A·B) / (||A|| ||B||)

余弦相似度是一种衡量两个向量在向量空间中夹角大小的方法。在二维空间中，我们可以将向量看作是从原点出发的箭头，而余弦相似度就是这两个箭头夹角的余弦值。这个值介于-1和1之间，值越大表示两个向量越相似，值越小表示两个向量越不相似。二、余弦相似度的计算余弦相似度的计算公式为：cos (θ) = (A·B) / (||A|| ||B||)，其中A和B是两个向量，||A||和||B||分别表示A和B的模（长度），A·B表示A和B的点积。

假设我们规定||A||和||B||分别表示A和B的模（长度）都是1，那么

Cos (θ) = (A·B)

相似度就是两个向量的点积。

qkv怎么来的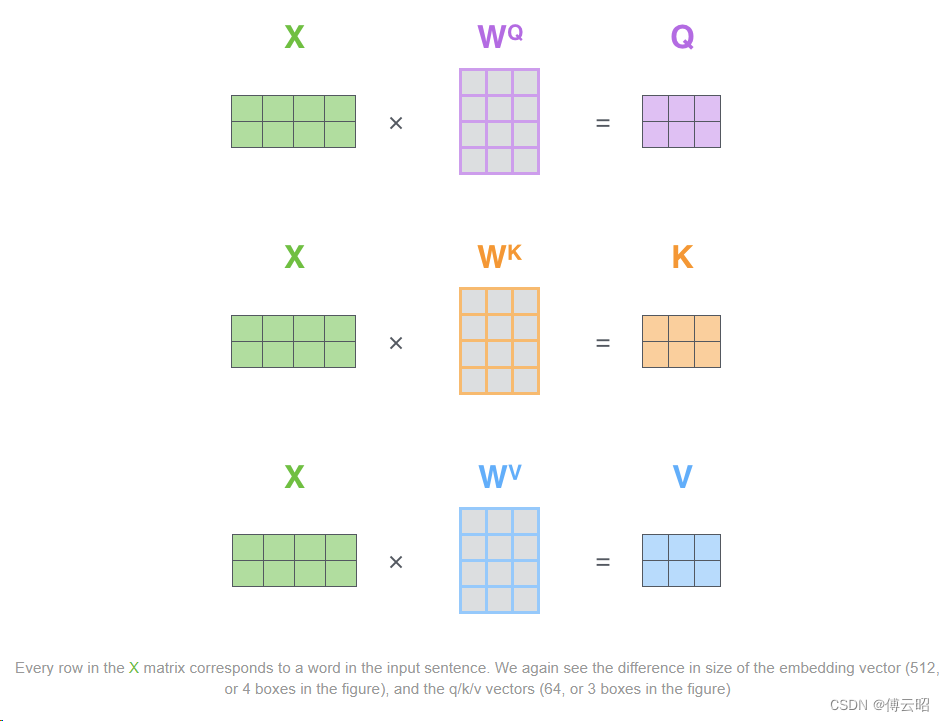

mlp实现的，conv1d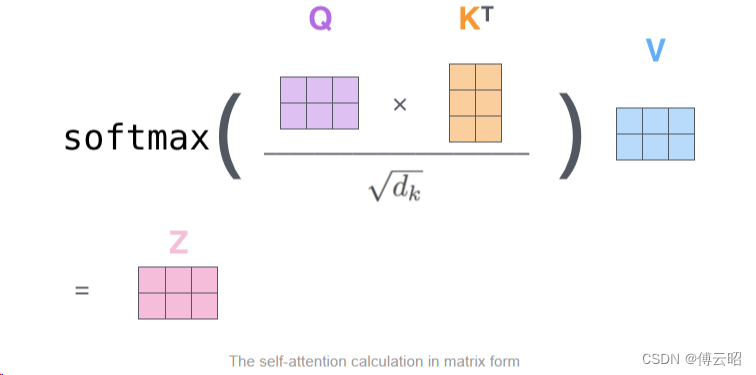

softmax：

Softmax函数是一个常用的数学函数，通常用于将一组实数转换为概率分布。Softmax函数接受一个实数向量作为输入，并将每个元素转换为非负数，使得所有元素之和等于1，表示它们在概率分布中的概率。

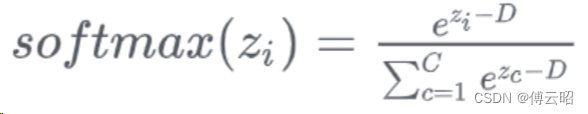
softmax(x) = [exp(x₁) / (exp(x₁) + exp(x₂) + ... + exp(xₙ)),exp(x₂) / (exp(x₁) + exp(x₂) + ... + exp(xₙ)),

...exp(xₙ) / (exp(x₁) + exp(x₂) + ... + exp(xₙ))]

例如：

计算的结果可能是一些其他值：21，6，3--》softmax:

Sum = e(21) + e(6) + e(3)

softmax(x1) = e(21) / sum

softmax(x2) = e(6) / sum

softmax(x3) = e(3) / sum

softmax(x) =[ e(21) / sum ,e(6) / sum , e(3) / sum ]

code

# attention
class ScaledDotProductAttention(nn.Module):""" Scaled Dot-Product Attention """def __init__(self, scale):super().__init__()self.scale = scaleself.softmax = nn.Softmax(dim=2)def forward(self, q, k, v, mask=None):u = torch.bmm(q, k.transpose(1, 2))  # 1.Matmul,(bs,2,4)u = u / self.scale  # 2.Scaleif mask is not None:mask[0,1,1] = 1u = u.masked_fill(mask, -np.inf)  # 3.Mask atten, e(-inf) = 0attn = self.softmax(u)  # 4.Softmax （bs,2,4）2query,4key, u:4*64,4key,64 lengthoutput = torch.bmm(attn, v)  # 5.Output：bs,2(query个数）,64（value长度）return attn, outputif __name__ == "__main__":batch  = 192# n_q, n_k, n_v = 2, 4, 4      # 2 query，4 key，4 value，总共2*4=8个weightn_q, n_k, n_v = 200, 480*640, 480*640      # 2 query，4 key，4 value，总共2*4=8个weightd_q, d_k, d_v = 128, 128, 64 ## n_q, n_k, n_v = 1208, 1208, 1208  # 2 query，4 key，4 value，总共2*4=8个weight# d_q, d_k, d_v = 64, 64, 64  #q = torch.randn(batch, n_q, d_q) # bs*2*128k = torch.randn(batch, n_k, d_k) # bs*4*128v = torch.randn(batch, n_v, d_v) # bs*4*64mask = torch.zeros(batch, n_q, n_k).bool()attention = ScaledDotProductAttention(scale=np.power(d_k, 0.5))  # scale是query和key长度128的根号attn, output = attention(q, k, v, mask=mask)

multi-head-attention

在传统的注意力机制中，给定一个查询（Query）和一组键值对（Key-Value Pairs），注意力机制通过计算查询与每个键之间的相关度，然后将这些相关度应用于对应值的加权和。这种单头的注意力机制可以捕捉到一种特定的关注模式，但可能无法充分表达序列中丰富的关系。

多头注意力通过引入多个子注意力头来解决这个问题。在每个子头中，通过对查询、键和值进行独立的线性变换，然后计算相应的注意力权重。最后，将所有子头的注意力权重加权和作为最终的输出。

具体来说，多头注意力可以分为以下几个步骤：

线性变换：对查询、键和值进行线性变换，将它们映射到不同的表示空间。这可以通过矩阵乘法实现，其中每个子头都有自己的权重矩阵。
注意力计算：对于每个子头，通过计算查询与键的内积，然后进行缩放（通常是除以查询维度的平方根），得到注意力得分。注意力得分可以表示查询与键的相关度。
注意力权重：通过将注意力得分经过 softmax 函数进行归一化，得到每个键的注意力权重。这些权重决定了对应值的重要程度。
加权和：将每个子头的注意力权重与对应的值相乘，然后将它们加权求和得到最终的输出表示。

多头注意力的优势在于它能够并行计算多个子头，从而提高模型的计算效率。同时，每个子头可以关注输入序列中不同的部分，从而捕捉到更丰富的关系。最终的输出表示将多个子头的信息整合在一起，以提供更全面的表示能力。

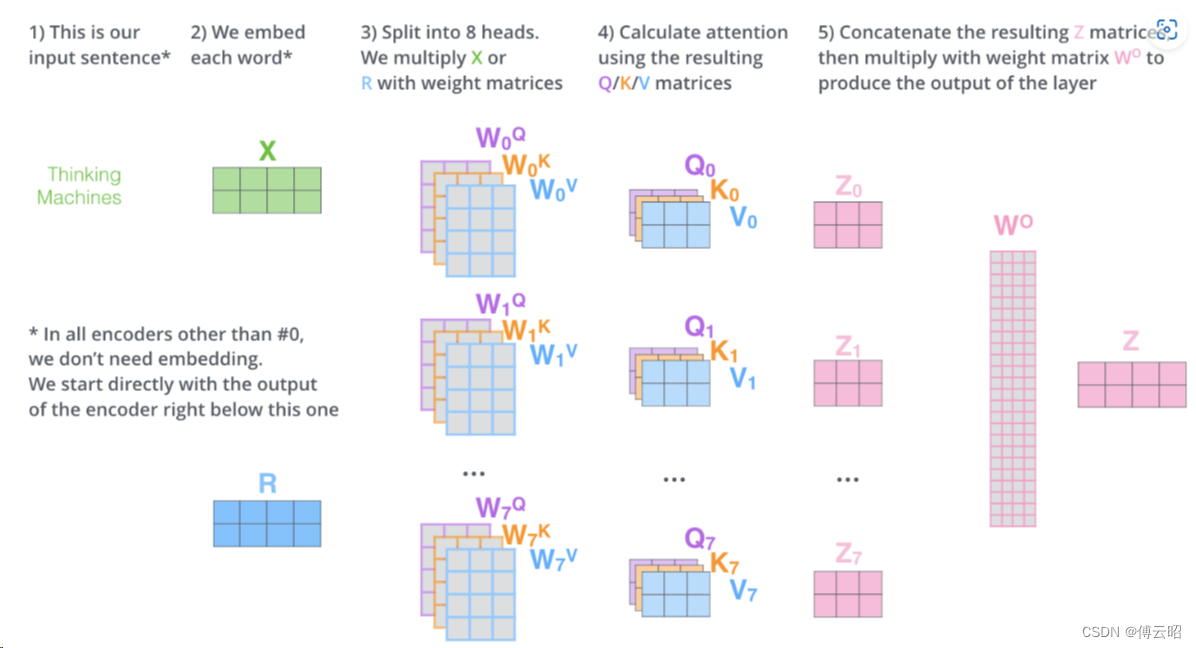
我可以把输入的x分解为一个qkv，也可以分解为8个qkv（8 heads）

多头的本质无非就是多了几组参数，模型参数越大，拟合能力越强

import torch.nn as nn
import torch
import numpy as np
from attention import ScaledDotProductAttentionclass MultiHeadAttention(nn.Module):""" Multi-Head Attention """def __init__(self, n_head, d_k_, d_v_, d_k, d_v, d_o):super().__init__()self.n_head = n_headself.d_k = d_kself.d_v = d_vself.fc_q = nn.Linear(d_k_, n_head * d_k)  # d_k_  = d_q_,  (128)d_k_ != d_k(256)self.fc_k = nn.Linear(d_k_, n_head * d_k)self.fc_v = nn.Linear(d_v_, n_head * d_v)self.attention = ScaledDotProductAttention(scale=np.power(d_k, 0.5))self.fc_o = nn.Linear(n_head * d_v, d_o)def forward(self, q, k, v, mask=None):n_head, d_q, d_k, d_v = self.n_head, self.d_k, self.d_k, self.d_vbatch, n_q, d_q_ = q.size()batch, n_k, d_k_ = k.size()batch, n_v, d_v_ = v.size()"""一组qkv(各自random来，可以不同) linear 多组 qkvq,k,v来自相同的x就是self-attention，否则就是cross attention"""q = self.fc_q(q)  # 1.单头变多头, (bs,2,128) -->(bs,2,2048) ,16倍k = self.fc_k(k)  # （bs,4,128） -->(bs,4,2048)v = self.fc_v(v)  # (bs,4,64) --> (bs,4,1024)q = q.view(batch, n_q, n_head, d_q).permute(2, 0, 1, 3).contiguous().view(-1, n_q, d_q)  # (8,2,256)k = k.view(batch, n_k, n_head, d_k).permute(2, 0, 1, 3).contiguous().view(-1, n_k, d_k)v = v.view(batch, n_v, n_head, d_v).permute(2, 0, 1, 3).contiguous().view(-1, n_v, d_v)if mask is not None:mask = mask.repeat(n_head, 1, 1)attn, output = self.attention(q, k, v, mask=mask)  # 2.当成单头注意力求输出output = output.view(n_head, batch, n_q, d_v).permute(1, 2, 0, 3).contiguous().view(batch, n_q, -1)  # 3.Concatoutput = self.fc_o(output)  # 4.仿射变换得到最终输出return attn, outputif __name__ == "__main__":batch = 2n_q, n_k, n_v = 2, 4, 4d_q_, d_k_, d_v_ = 128, 128, 64# 192，1408q = torch.randn(batch, n_q, d_q_)k = torch.randn(batch, n_k, d_k_)v = torch.randn(batch, n_v, d_v_)mask = torch.zeros(batch, n_q, n_k).bool()mha = MultiHeadAttention(n_head=8, d_k_=128, d_v_=64, d_k=256, d_v=128, d_o=128)attn, output = mha(q, k, v, mask=mask)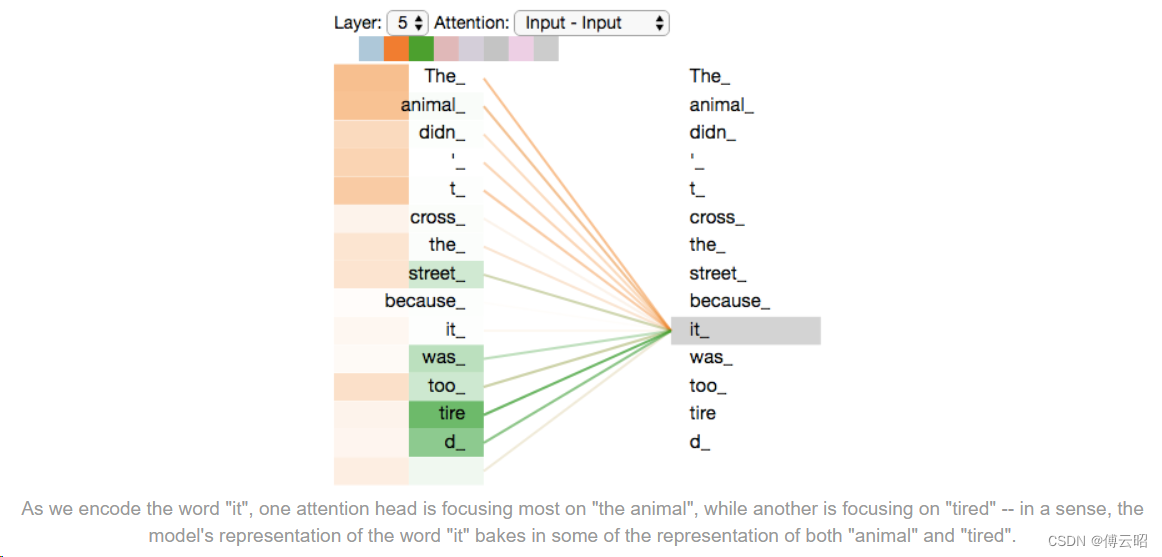

在对单词"it"进行编码时，一个注意力头（attention head）主要关注"the animal"，而另一个注意力头则主要关注"tired"。从某种意义上说，模型对单词"it"的表示融入了"animal"和"tired"两个单词的一些表示信息。

这种现象是由于自注意力机制的特性所导致的。在自注意力机制中，每个单词都可以与其他单词进行交互，并根据其在句子中的上下文关系来计算权重。在编码单词"it"时，注意力头会根据输入句子的整体语义进行选择性地关注相关的单词。

因此，一个注意力头可能更关注与"it"在语义上相关的"the animal"，而另一个注意力头则更关注与"it"在语义上相关的"tired"。这种注意力分配的机制使得模型在表示"it"时同时包含了与"the animal"和"tired"相关的一些信息。

通过这种方式，模型可以在编码过程中将相关的上下文信息融入到每个单词的表示中，从而更好地捕捉单词之间的语义关联。这种融合的表示有助于提高模型对整个句子的理解和语义表达能力。

位置编码：

位置编码是一种用于为序列数据中的每个位置赋予特定的编码信息的技术。在自注意力机制（如Transformer模型）中，位置编码被用于为输入序列中的每个单词或位置赋予其相对位置的信息，这样模型可以利用这些位置信息来更好地建模单词之间的顺序关系。

在Transformer模型中，常用的位置编码方法是使用正弦和余弦函数来生成位置向量。具体而言，对于序列中的每个位置i和每个维度j，位置编码向量PE(i, j)可以通过以下公式计算得到：

PE(i, 2j) = sin(i / 10000^(2j/d_model))

PE(i, 2j+1) = cos(i / 10000^(2j/d_model))

其中，i表示位置，j表示维度，d_model表示模型的维度。通过这种方式，位置编码向量中的奇数维度用正弦函数编码，偶数维度用余弦函数编码。这样，不同位置的位置编码向量在不同维度上的数值差异可以反映出它们之间的相对位置关系。

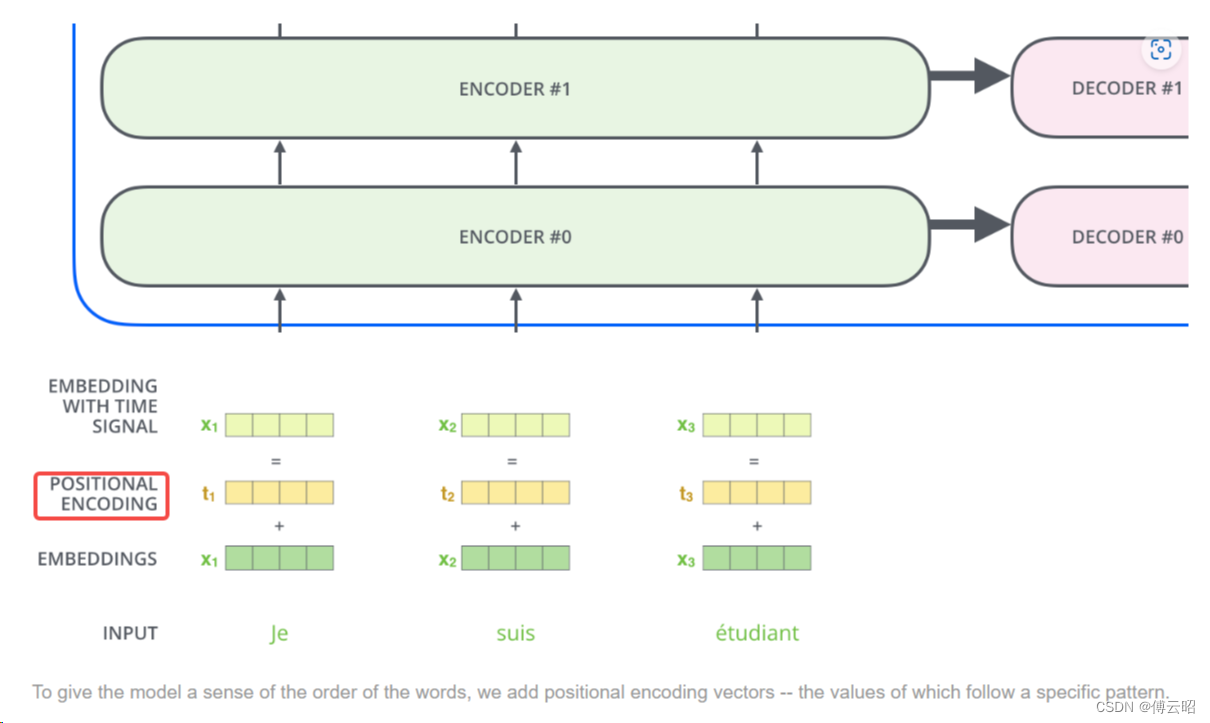
位置编码向量可以与输入的词向量相加，从而将位置信息融入到词向量中。这样，模型在进行自注意力计算时不仅考虑单词的语义信息，还会考虑它们在序列中的相对位置关系。位置编码的引入有助于模型更好地捕捉序列数据中的顺序信息，提高模型对序列的理解能力。

需要注意的是，位置编码是在模型的输入阶段添加的，它不会随着训练而更新。它提供了一种固定的表示方式，用于传达位置信息给模型。

该算法使用正弦和余弦函数来生成位置编码向量，具有以下几个原因：

周期性：正弦和余弦函数具有周期性的特性，可以在位置编码中表达不同位置之间的相对距离。通过使用这两个函数，我们可以创建一种循环的模式，使得相同距离的位置在编码向量中具有相似的值。
连续性：正弦和余弦函数是连续的函数，可以提供平滑的变化。这样，在相邻位置之间的微小变化也可以在位置编码中得到对应的微小变化，从而更好地捕捉到位置之间的细微差异。
兼容性：位置编码算法与Transformer模型的自注意力机制相兼容。在自注意力计算中，位置编码向量可以与输入的词向量相加，从而将位置信息融入到模型中。由于正弦和余弦函数的周期性和连续性特征，位置编码向量与词向量的加和操作可以保持一定的平衡，不会引入过大的变动。

假设我们仍然使用示例中的文本序列："I love natural language processing."，并假设d_model为4。

对于单词"I"，我们计算其位置编码向量。

对于每个位置i和每个维度j，位置编码向量PE(i, j)可以通过以下公式计算得到：

每个位置i一般的维度都是64？dimension是512？

位置1的位置编码向量 PE(1, 0)：

PE(1, 0) = sin(1 / 10000^(0/4))

= sin(1 / 10000^0)

= sin(1 / 1)

= sin(1)

≈ 0.8415

位置1的位置编码向量 PE(1, 1)：

PE(1, 1) = cos(1 / 10000^(1/4))

= cos(1 / 10000^0.25)

= cos(1 / 1.7783)

≈ cos(0.5623)

≈ 0.8253

对于单词"love"，我们同样计算其位置编码向量。

位置2的位置编码向量 PE(2, 0)：

PE(2, 0) = sin(2 / 10000^(0/4))

= sin(2 / 10000^0)

= sin(2 / 1)

= sin(2)

≈ 0.9093

位置2的位置编码向量 PE(2, 1)：

PE(2, 1) = cos(2 / 10000^(1/4))

= cos(2 / 10000^0.25)

= cos(2 / 1.7783)

≈ cos(1.1246)

≈ 0.4546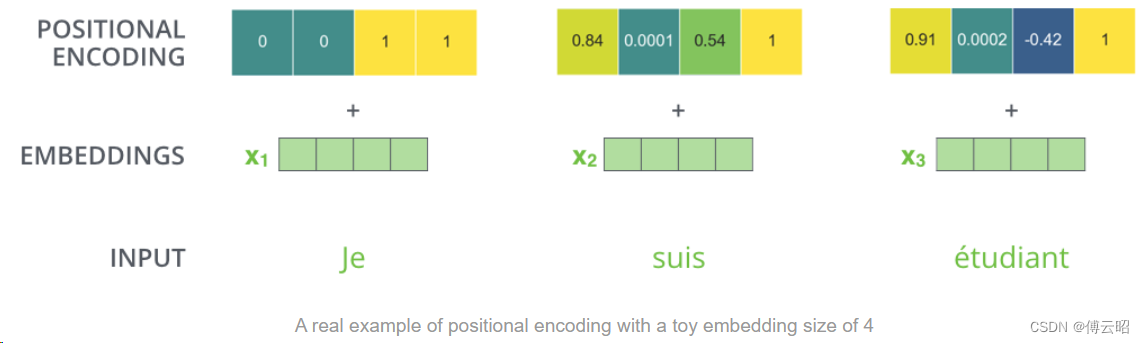

class PositionalEncoding(nn.Module):def __init__(self, d_hid, n_position=200):super(PositionalEncoding, self).__init__()# Not a parameter# 将tensor注册成buffer, optim.step()的时候不会更新self.register_buffer('pos_table', self._get_sinusoid_encoding_table(n_position, d_hid))def _get_sinusoid_encoding_table(self, n_position, d_hid):''' Sinusoid position encoding table '''# TODO: make it with torch instead of numpydef get_position_angle_vec(position):# 2i, 所以此处要//2. return [position / np.power(10000, 2 * (hid_j // 2) / d_hid) for hid_j in range(d_hid)]sinusoid_table = np.array([get_position_angle_vec(pos_i) for pos_i in range(n_position)])sinusoid_table[:, 0::2] = np.sin(sinusoid_table[:, 0::2])  # dim 2i 偶数sinusoid_table[:, 1::2] = np.cos(sinusoid_table[:, 1::2])  # dim 2i+1 奇数return torch.FloatTensor(sinusoid_table).unsqueeze(0) # shape:(1, maxLen(n_position), d_hid)def forward(self, x):return x + self.pos_table[:, :x.size(1)].clone().detach() # 数据、梯度均无关

残差&&FFN：

Transformer模型中的残差连接是一种技术，用于在不同层之间传递信息并减轻梯度消失的问题。它通过将输入信号与层内计算的结果相加，从而将原始输入的信息直接传递到网络的后续层。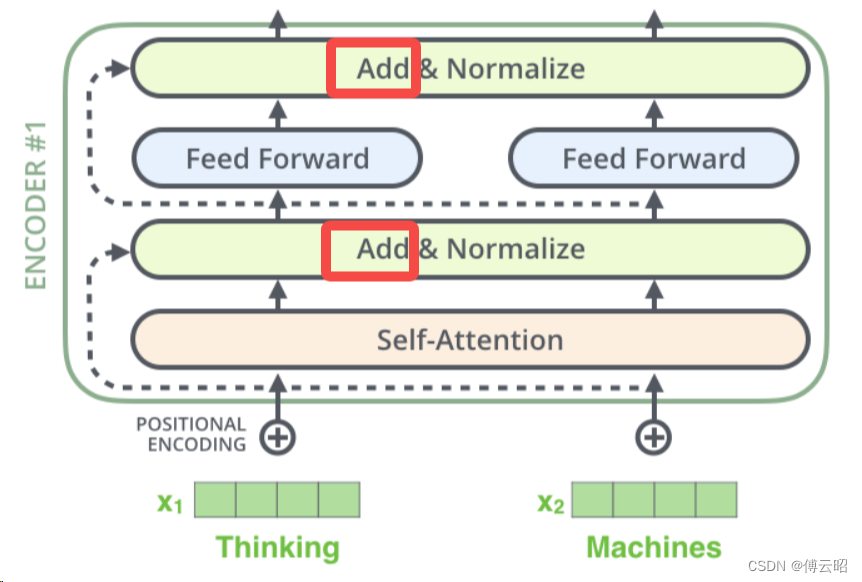

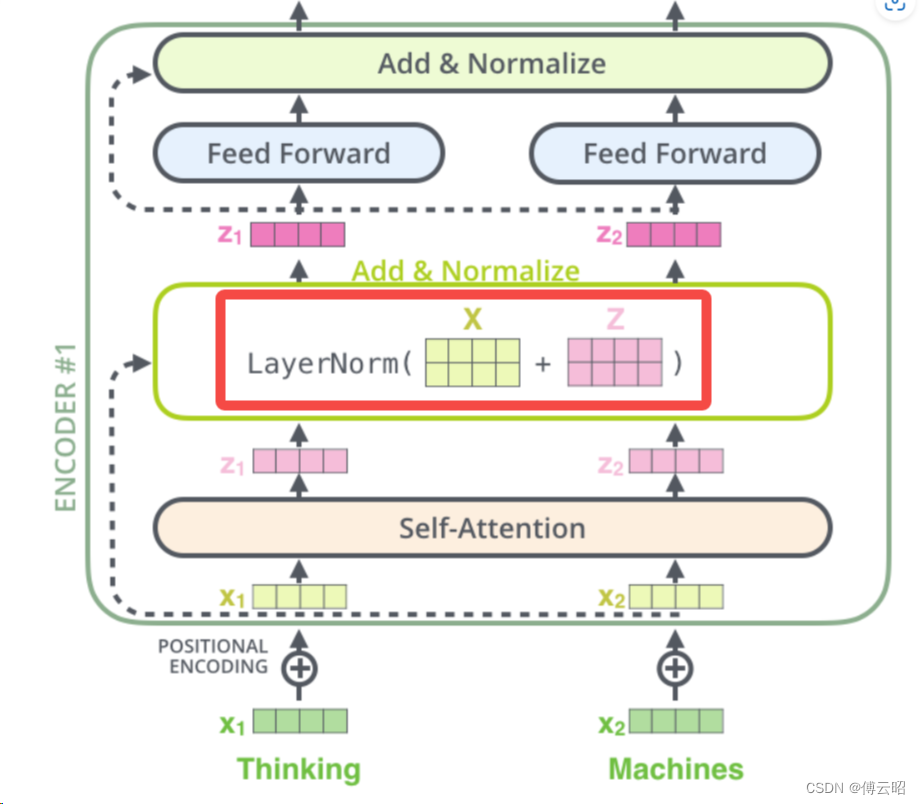
class PositionwiseFeedForward(nn.Module):''' A two-feed-forward-layer module '''def __init__(self, d_in, d_hid, dropout=0.1):super().__init__()self.w_1 = nn.Linear(d_in, d_hid) # position-wiseself.w_2 = nn.Linear(d_hid, d_in) # position-wiseself.layer_norm = nn.LayerNorm(d_in, eps=1e-6)self.dropout = nn.Dropout(dropout)def forward(self, x):residual = xx = self.w_2(F.relu(self.w_1(x)))x = self.dropout(x)# add & normx += residualx = self.layer_norm(x)return x

decoder：

在Transformer解码器中，它采用了自注意力机制（self-attention）和多头注意力机制（multi-head attention）来编码输入序列的上下文信息，并利用位置编码对序列中的位置信息进行建模。解码器通过逐步进行自注意力计算和前馈神经网络（Feed-Forward Network）的处理，生成目标序列的每个元素。

cross-attention

解码器的目标是根据输入的上下文信息和先前生成的元素，以逐步生成目标序列。它可以根据任务的不同而有所调整，例如在机器翻译任务中，解码器可以逐步生成目标语言的单词；在图像生成任务中，解码器可以逐步生成图像的像素值。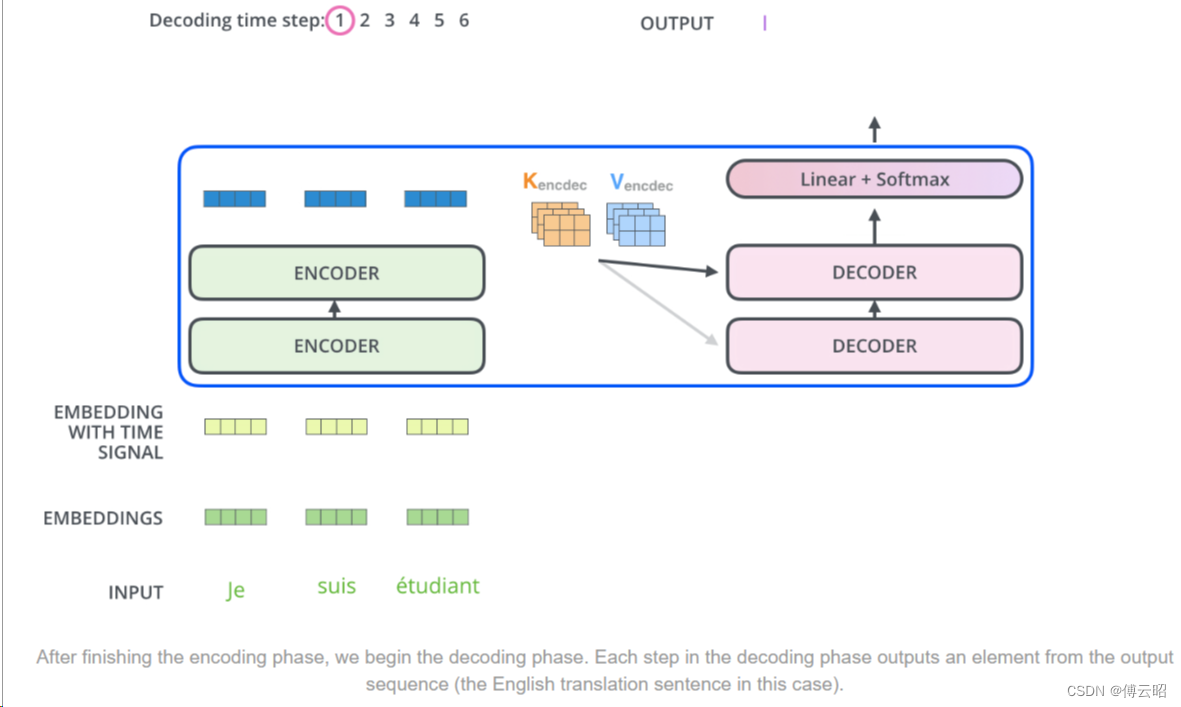

kv来自encoder，q来自decoder

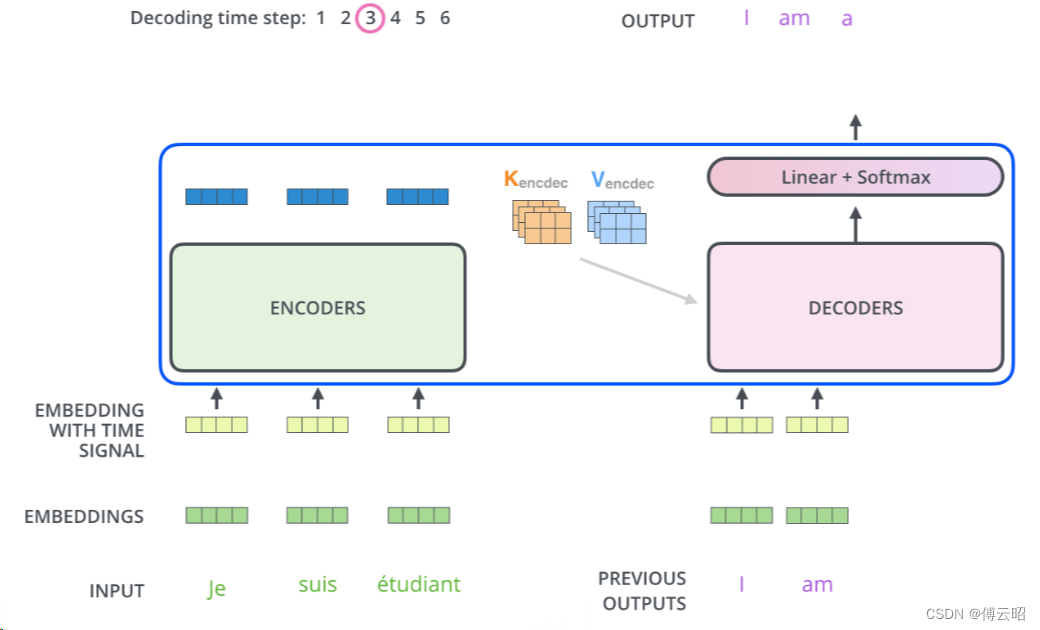
在解码器中，输出的每一步会被作为下一个时间步骤中底层解码器的输入，并且解码器会像编码器一样将其解码结果向上传递。与编码器输入类似，解码器输入也会经过嵌入和位置编码的处理，以指示每个单词的位置。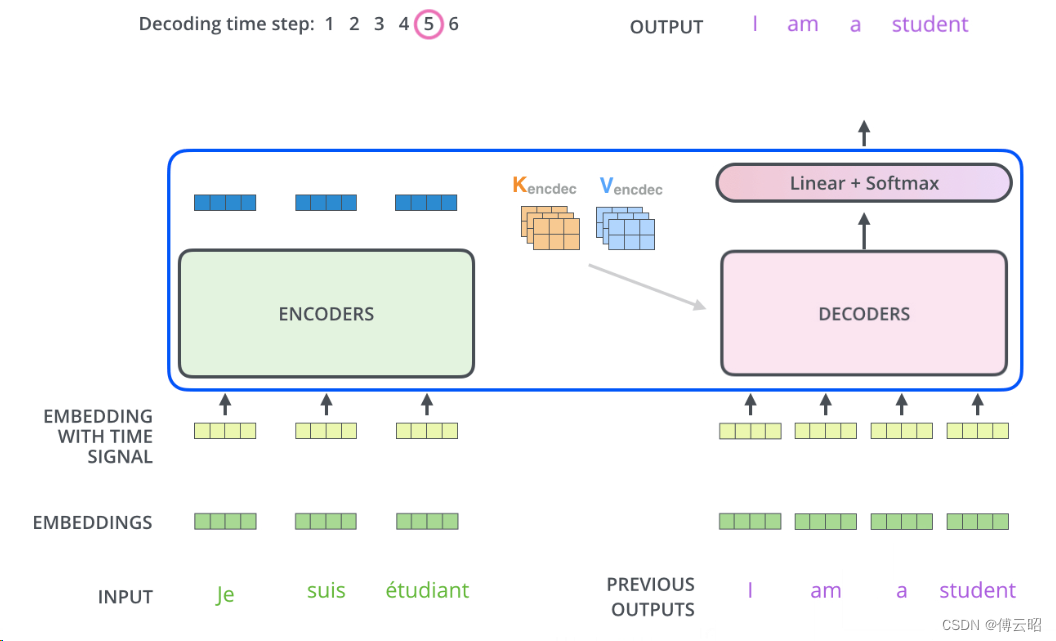

self-attention

在Transformer解码器中，自注意力层的操作方式与编码器中的略有不同：

在解码器中，自注意力层只能关注输出序列中的先前位置（单向attention，encoder的attention是双向的，即后中间的单词既可以和前面又可以和后面的词attention，而decoder中的只能和前面的词attention）。为了实现这一点，在自注意力计算中，在进行softmax之前，将未来位置进行掩码（将其设置为负无穷）。

过程就是mask住下一个词和他后面的词，预测下一个词，然后把预测的下一个词作为输入在预测下一个词。

Linear + softmax

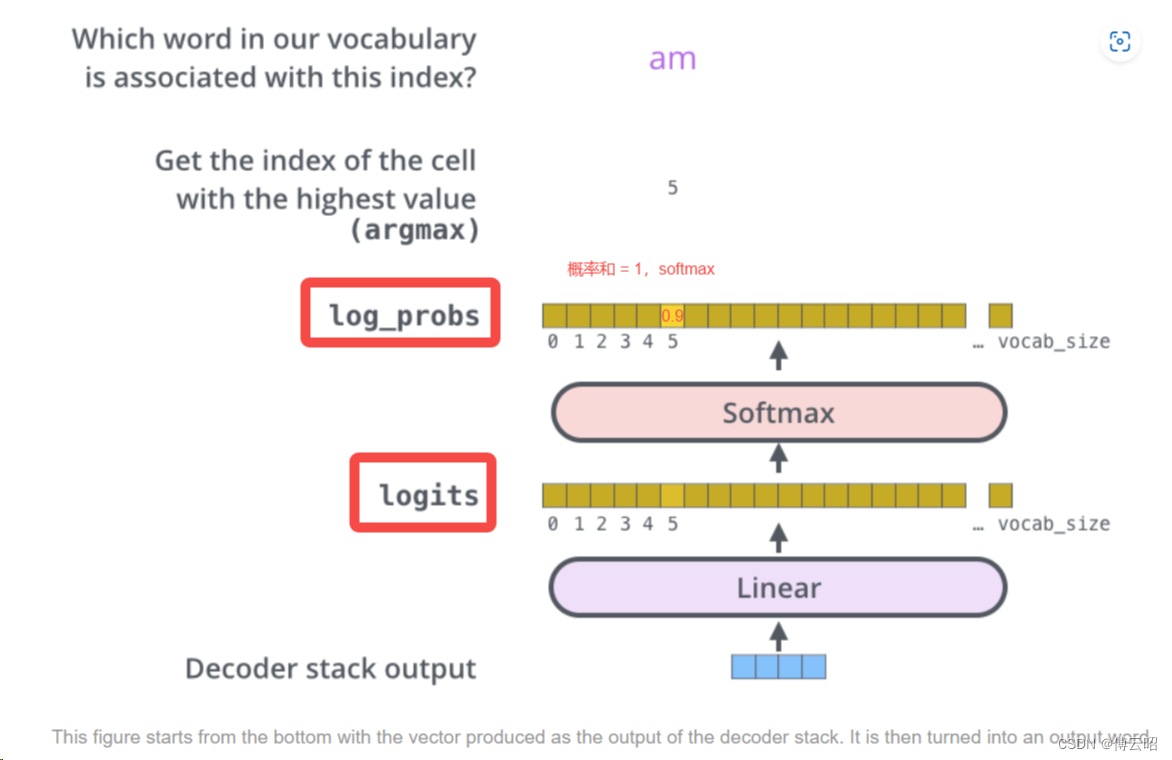
在Transformer解码器中，解码器堆栈的输出是一个浮点数向量。我们如何将其转换为单词？这是最终的线性层和其后的Softmax层的任务。

线性层是一个简单的全连接神经网络，将解码器堆栈生成的向量投影到一个更大的向量中，称为logits向量。

假设我们的模型知道10,000个唯一的英文单词（模型的“输出词汇表”），这些单词是从训练数据集中学习得到的。这将使logits向量的宽度为10,000个单元格，每个单元格对应一个唯一单词的分数。这就是我们如何解释线性层之后的模型输出。

然后，Softmax层将这些分数转换为概率（都是正数，总和为1.0）。选择具有最高概率的单元格，并将与之相关联的单词作为该时间步骤的输出生成。

简而言之，通过线性层和Softmax层，将解码器堆栈的输出转换为概率分布，并根据最高概率选择输出的单词。

Train&&loss

训练过程中，未经训练的Transformer模型也会经历完全相同的前向传播过程。但由于我们在带标签的训练数据集上进行训练，我们可以将模型的输出与实际正确输出进行比较。

为了可视化这一点，让我们假设我们的输出词汇表只包含六个单词（"a"，"am"，"i"，"thanks"，"student"和"<eos>"，表示句子的结束）。

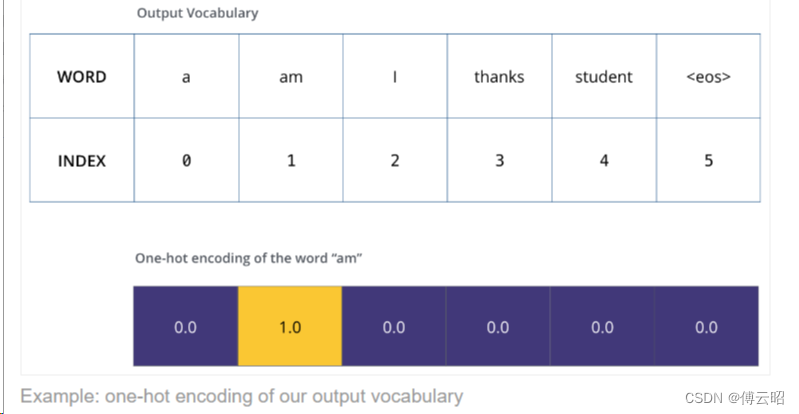
假设我们正在训练我们的模型，这是训练阶段的第一步，我们正在使用一个简单的例子进行训练——将"merci"翻译成"thanks"。

这意味着我们希望输出是一个概率分布，指示单词"thanks"。但由于这个模型尚未经过训练，目前实现这一点的可能性较低。

在训练的初始阶段，模型的参数是随机初始化的，它对输入序列"merci"的翻译可能会得到不正确的输出。由于模型尚未学习到正确的翻译关系，输出的概率分布可能会在词汇表中的不同单词上分散，而不是集中在"thanks"上。

通过训练过程中的反向传播和参数更新，模型逐渐学习到输入序列"merci"与目标序列"thanks"之间的对应关系，并且输出概率分布逐渐偏向于正确的单词。随着训练的进行，模型的输出将逐渐接近我们所期望的目标。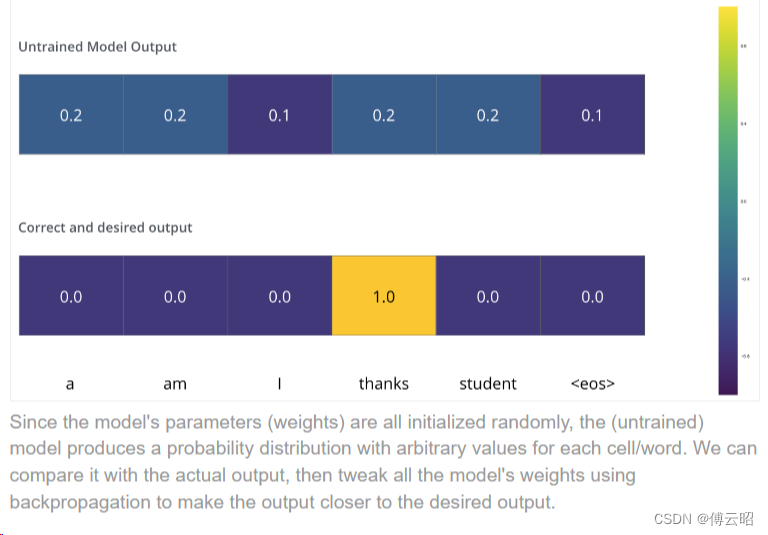

要比较两个概率分布，我们可以简单地将一个概率分布减去另一个概率分布。有关更多详细信息，请参考交叉熵和Kullback-Leibler散度。

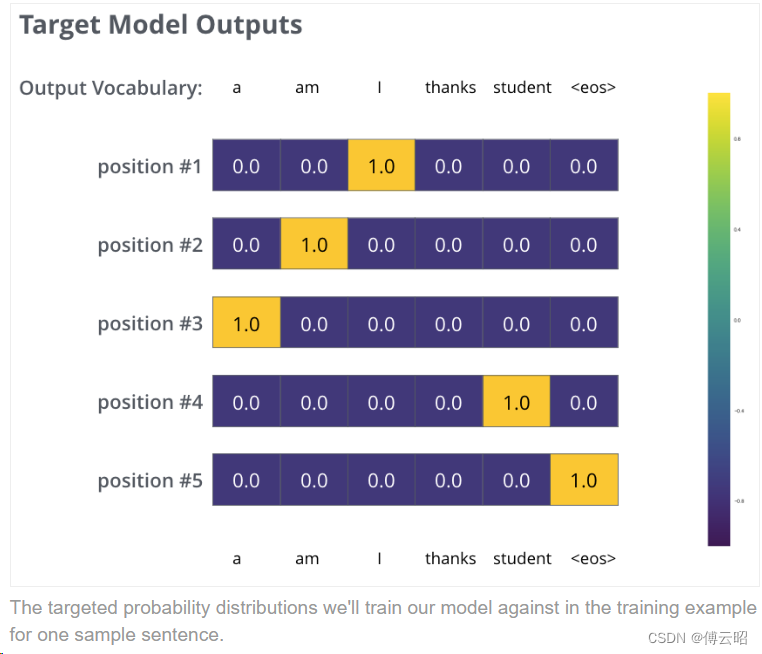
但请注意，这只是一个过度简化的例子。更实际地说，我们将使用长度超过一个单词的句子。例如，输入为"je suis étudiant"，期望输出为"i am a student"。这实际上意味着我们希望我们的模型连续输出概率分布，其中：

每个概率分布由宽度为vocab_size的向量表示（在我们的玩具示例中为6，但更实际地可能是30,000或50,000等数字）。
第一个概率分布在与单词"i"相关的单元格中具有最高的概率。
第二个概率分布在与单词"am"相关的单元格中具有最高的概率。
依此类推，直到第五个输出分布指示了'<end of sentence>'符号，该符号在由10,000个元素构成的词汇表中也有一个单元格与之对应。

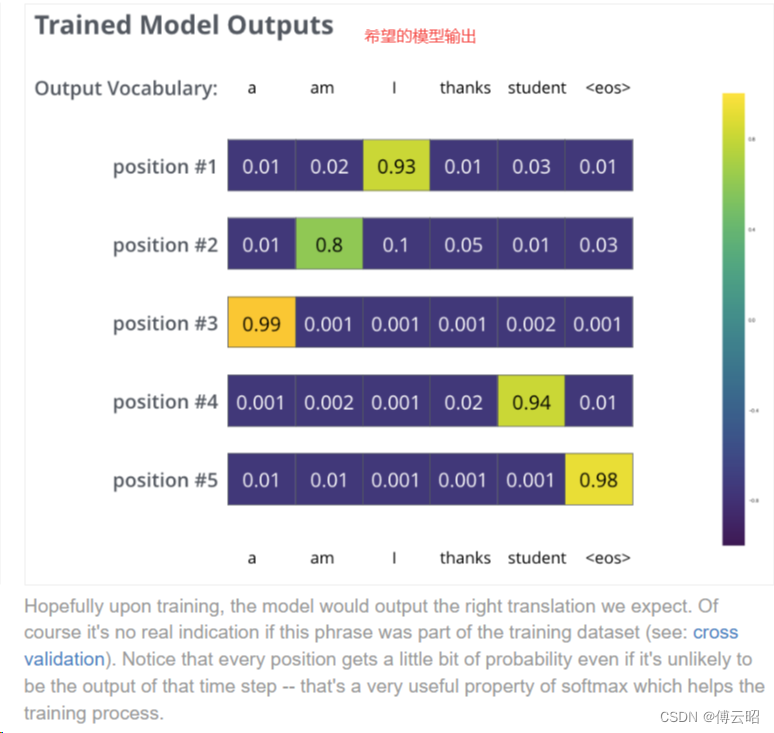
在生成输出时，模型可以一次选择具有最高概率的单词，并忽略其他单词，这被称为贪婪解码。这是一种方法。另一种方法是保留前两个最高概率的单词（例如，'I'和'a'），然后在下一步中运行模型两次：一次假设第一个输出位置为单词'I'，另一次假设第一个输出位置为单词'a'，并且考虑到位置#1和#2，选择产生较少错误的版本。我们对位置#2、#3等进行类似的操作。这种方法称为"beam search"，在我们的示例中，beam_size为2（表示始终保留两个未完成翻译的假设），top_beams也为2（表示我们将返回两个翻译结果）。这些都是您可以进行实验的超参数。

通过使用beam search，可以在生成过程中保留多个可能的翻译假设，而不仅仅是贪婪地选择单个单词。这有助于处理复杂的输出空间，提高模型生成正确翻译的概率。您可以根据任务的要求和实际情况对beam_size和top_beams进行调整和优化。