朴素贝叶斯
特征为理想状态下的独立同分布,作为机器学习的重要基石和工具
由贝叶斯公式推导而来
是后验概率:在B发生的条件下A发生的概率。
是似然概率: 在
发生的条件下
发生的概率。
是先验概率:
发生的概率,而不考虑
的影响。
是边缘概率:
发生的概率, 而不考虑
的影响。
这种不考虑相互之间的影响,并不是说AB没有任何关系,只是说客观条件下发生的A和B的概率分别是多少
贝叶斯定理的直观理解
假设A代表某种特定情况或假设,比如某人患有一种疾病,而B代表一个相关观测或数据,比如一个医学检测的结果。贝叶斯定理允许我们使用检测结果来更新我们对该人患病概率的估计。
先验摡率 :在没有看到检测结果之前,我们对疾病的概率评估。
似然摡率 :如果该人确实患病,得到当前检测结果的概率。
边缘摡率 :任何情况下得到这个检测结果的总概率。
后验摡率 : 在检测结果呈阳性后,该人实际患病的概率。
朴素贝叶斯在贝叶斯定理基础上:
-
特征独立性假设:朴素贝叶斯分类器假设所有的特征在给定类别的条件下都是相互独立的。因此,一个实例的类别概率可以通过将其所有单独特征的概率相乘得到。
-
模型训练与预测:在训练阶段,算法将通过训练数据学习每个类别的先验概率(即每个类别在数据中出现的频率)和每个特征在给定类别下的概率。在预测阶段,算法利用这些学习到的概率和贝叶斯定理来计算给定实例属于每个类别的概率,最后将实例分类到具有最高后验概率的类别。
应用场景:
朴素贝叶斯因其简单性、速度快和适应性强,在文本分类(如垃圾邮件识别、情感分析)、医疗诊断、用户行为预测等多个领域都有广泛的应用。尽管“朴素”的独立性假设很少在实际数据中完全成立,但在实践中,朴素贝叶斯仍然能够提供强大的基准性能。
朴素贝叶斯的优点:
对小规模的数据表现很好,适合多分类任务,适合增量式训练。
缺点:
对输入数据的表达形式很敏感。
决策树
举个栗子:
假设我们有一个数据集,我们想根据天气条件来决定是否进行野餐。
我们的数据集包含以下特征:
- 天气(晴朗、多云、下雨)
- 温度(热、温暖、凉爽)
- 湿度(高、正常)
- 风力(强、弱)
目标变量是决定是否进行野餐(是、否)。
假设我们有以下训练数据:
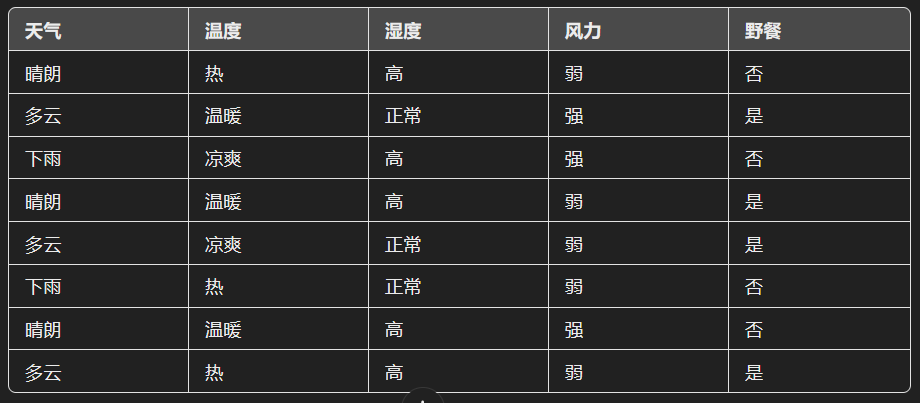
接下来,我们根据天气的不同值(晴朗、多云、下雨)分三个分支:
-
如果天气是晴朗,我们进一步观察数据,发现当风力是弱时,我们通常会选择进行野餐,但如果风力强,则不去。因此,在“晴朗”分支下,我们创建一个基于“风力”的决策节点。
-
如果天气是多云,我们观察到无论其他条件如何,结果似乎总是“是”,所以这个分支直接结束在一个叶节点上,表示决定“进行野餐”。
-
如果天气是下雨,数据显示我们通常不去野餐,所以这个分支也直接结束在一个叶节点上,表示决定“不进行野餐”。
最终,我们得到一个决策树,其中包括决策点(天气和风力)和决策结果(是否进行野餐)。在实际应用中,当我们有一个新的天气预报时,我们可以根据这个决策树来决定是否安排野餐。
决策树的工作原理:
- 节点分裂:从数据集的根部开始,选择最佳特征来分割数据,以便于按照某种标准优化目标函数(如信息增益、增益比率或基尼不纯度)。这个过程将重复进行,每一步都选择最佳特征来进一步将数据子集分割成更小的子集。
- 树的构建:通过重复分裂过程,决策树将不断生长,直到满足某些停止条件,例如树达到最大深度、节点下的样本数少于最小样本数、或者如果进一步分割不能增加信息增益。
- 剪枝:为了防止过拟合,决策树的生长可能会通过剪枝过程被停止,其中一些子树会被替换为叶节点。剪枝可以在树完全生长后进行(后剪枝),也可以在树构建过程中进行(预剪枝)。
决策树的主要优点:
- 直观性:决策树的结果很容易理解和解释,可以可视化展示。
- 无需数据预处理:决策树通常不需要数据归一化,也不需要处理缺失值。
- 适用性广:可以处理数值型和类别型数据,也适用于多类别分类。
决策树的不足:
- 过拟合:决策树很容易过拟合,尤其是当树很深时,它可能会学习到数据中的噪声。可以通过设置树深度限制、要求一个节点包含的最小样本数或剪枝等方法来缓解过拟合。
- 稳定性:决策树对数据中的小变动可能很敏感,这可能导致生成完全不同的树。这个问题可以通过集成方法,如随机森林,来缓解。
Logistics回归和线性回归跳过
KNN算法
假设我们有一个简化的情况:我们需要根据电影的“打斗场景数”和“接吻场景数”来判断电影是动作片还是爱情片。
假设我们的训练数据集如下:
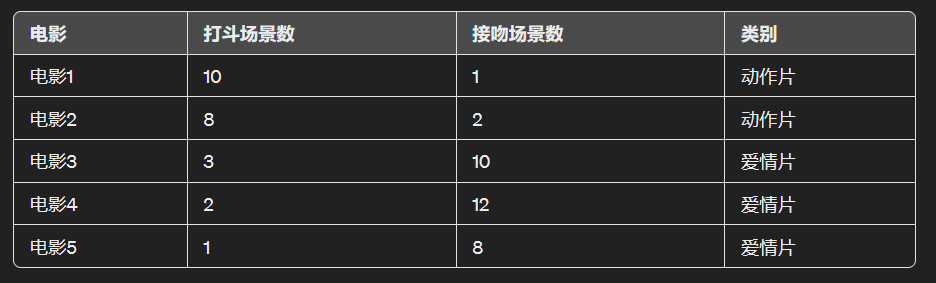
现在,假设我们有一个新电影(未知类别)的数据如下:

首先,我们需要决定如何测量距离。在这个例子中,我们可以使用欧几里得距离。对于电影1,距离会是:
我们对每部电影重复这个过程,找出与未知电影最近的三部电影。假设它们是电影1、电影2和电影3(这只是一个例子,实际结果取决于计算出的实际距离)。
接下来,我们看这三部最近的电影分别属于哪些类别。假设电影1和电影2是动作片,电影3是爱情片。
因为在最近的三部电影中,有两部是动作片,一部是爱情片,所以根据k-NN算法,我们会预测未知电影也是动作片。
我们要使用k-NN算法来预测这部未知电影的类别。我们选择 k = 3,意味着我们将查看距离未知电影最近的三部电影。
-
首先,我们需要决定如何测量距离。在这个例子中,我们可以使用欧几里得距离。对于电影1,距离会是:
KNN即最近邻算法,其主要过程为:
1. 计算训练样本和测试样本中每个样本点的距离(常见的距离度量有欧式距离,马氏距离等);
2. 对上面所有的距离值进行排序;
3. 选前k个最小距离的样本;
4. 根据这k个样本的标签进行投票,得到最后的分类类别;
如何选择一个最佳的K值,这取决于数据。一般情况下,在分类时较大的K值能够减小噪声的影响。但会使类别之间的界限变得模糊。一个较好的K值可通过各种启发式技术来获取,比如,交叉验证。另外噪声和非相关性特征向量的存在会使K近邻算法的准确性减小。
近邻算法具有较强的一致性结果。随着数据趋于无限,算法保证错误率不会超过贝叶斯算法错误率的两倍。对于一些好的K值,K近邻保证错误率不会超过贝叶斯理论误差率。
KNN算法的优点:
1. 思想简单,理论成熟,既可以用来做分类也可以用来做回归;
2. 可用于非线性分类;
3. 训练时间复杂度为O(n);
4. 准确度高,对数据没有假设,对outlier不敏感;
缺点:
1. 计算量大;
2. 样本不平衡问题(即有些类别的样本数量很多,而其它样本的数量很少);
3. 需要大量的内存;
SVM
SVM就是简单来说就是分割高维平面来进行分类:
举个栗子来进行说明:
1. 最大边距超平面:
在二维空间中,一个超平面是一条直线,定义为,其中:
- ww 是法向量,决定了超平面的方向。
- xx 是任意点在平面上的位置。
- bb 是位移项,决定了超平面与原点的距离。
对于二分类问题,我们的目标是找到一个超平面,使得所有正样本(比如类别 +1)都满足 ,所有负样本(比如类别 -1)都满足
。
两个边界(对正样本和负样本)分别为:
- 正样本边界:
- 负样本边界:
这两个边界之间的距离叫做“边距”,可以计算为:
边距
在SVM中,我们的目标是最大化这个边距,从而创建最优的分割超平面。
2. 优化问题:
最大化边距 等价于最小化
。因此,我们可以写出以下优化问题:
受到以下约束条件:
这里, 是样本
的类别标签,取值为+1或-1。
3. 拉格朗日乘数法:
为了解决这个约束优化问题,我们使用拉格朗日乘数法将原问题转换为拉格朗日对偶问题,使得原问题和对偶问题达到同样的最小值。拉格朗日函数是:
其中,是拉格朗日乘数,对每一个数据点
都有一个对应的
。
4. 对偶问题:
通过对拉格朗日函数 关于
和
的偏导数等于0的条件,我们可以找到最优值
和
的表达式,并将它们代回拉格朗日函数,这将转换成只关于
的问题,这就是所谓的对偶问题。
最终,对偶问题可以写成:
受到约束:
解决这个对偶问题将给出所有拉格朗日乘数的最优值。最优的
可以通过已解决的
计算
SVM算法优点:
可用于线性/非线性分类,也可以用于回归;
低泛化误差;
容易解释;
计算复杂度较低;
缺点:
对参数和核函数的选择比较敏感;
原始的SVM只比较擅长处理二分类问题;
Boosting
Boosting是一种强大的集成学习策略,它基于这样一个原则:将多个弱学习器(通常指那些只比随机猜测略好的模型,如小决策树)组合起来,形成一个强学习器(即性能非常好的模型)。这个过程是通过迭代地训练弱学习器来完成的,每一轮的训练都侧重于之前被模型误分类的样本,从而使模型能够学习到数据的不同方面。
工作原理:
-
初始化权重:首先,对训练数据中的每个样本分配一个初始权重。在第一轮中,通常给所有样本相同的权重,比如 1/N,其中 N 是样本的数量。
-
迭代训练:在每一轮中,训练一个弱学习器,通常是决策树。该学习器是根据当前的数据权重分布进行训练的。
-
权重更新:一旦训练了一个弱学习器,就根据它的错误率来更新训练样本的权重:正确分类的样本权重降低,而错误分类的样本权重增加。这就意味着在下一轮中,新的弱学习器将更加关注那些之前被错误分类的样本。
-
模型组合:每个弱学习器会根据其性能(通常是它的错误率或损失)被赋予一个权重。最终的模型是所有这些弱学习器的加权组合,其中表现较好的模型会有更大的权重。
特点和优势:
-
性能:Boosting通常可以显著提高学习算法的性能,特别是对于复杂的任务,它能够减少偏差和方差,是一种有效的偏差-方差权衡策略。
-
灵活性:它可以与各种类型的学习算法结合使用,不仅限于决策树。
-
适应性:通过逐步地“学习”数据的不同方面(特别是通过更加关注那些难以正确分类的样本),Boosting算法可以适应复杂的数据结构。
著名的Boosting算法:
-
AdaBoost (Adaptive Boosting):最著名的Boosting算法之一,根据之前弱学习器的错误率来调整样本权重和学习器权重。
-
Gradient Boosting:另一种流行的Boosting方法,通过关注前一个模型的残差(即错误)来训练后续模型。
-
XGBoost、LightGBM、CatBoost:这些都是基于Gradient Boosting的高性能算法,广泛应用于数据科学竞赛和工业应用中,因其出色的速度和性能而闻名。
Boosting方法特别适合于处理偏差较大的情况,即那些在训练数据上欠拟合的情况。通过聚焦于难以正确分类的样本,Boosting能够创建一个更加准确和鲁棒的模型。
k-means自监督聚类
1. 初始化:
- 选择 k 个随机点作为簇中心(质心)。这些可以是随机选择的数据点,或者完全随机的位置。
- k 的选择依赖于数据及你希望识别的簇的数量,通常需要通过多次实验或其他方法(如肘部法则)来确定。
2. 分配步骤:
- 对于数据集中的每一个点,计算它与各个簇中心的距离,并将它分配到最近的簇中心所代表的簇。
- 最常用的距离度量是欧几里得距离,但也可以根据问题的特定需求选择其他类型的距离。
3. 更新步骤:
- 一旦所有的点都被分配到某个簇,每个簇的中心就会更新为该簇所有点的均值。这意味着簇中心将移动到它所有成员的平均位置。
4. 迭代:
- 重复分配和更新步骤,直到满足停止条件,例如:
- 簇中心的变化小于某个阈值;
- 达到预定的迭代次数;
- 数据点的簇分配不再改变。
k-means算法的优点:
(1)k-means算法是解决聚类问题的一种经典算法,算法简单、快速。
(2)对处理大数据集,该算法是相对可伸缩的和高效率的,因为它的复杂度大约是O(nkt),其中n是所有对象的数目,k是簇的数目,t是迭代的次数。通常k<<n。这个算法通常局部收敛。
(3)算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的,且簇与簇之间区别明显时,聚类效果较好。
缺点:
(1)k-平均方法只有在簇的平均值被定义的情况下才能使用,且对有些分类属性的数据不适合。
(2)要求用户必须事先给出要生成的簇的数目k。
(3)对初值敏感,对于不同的初始值,可能会导致不同的聚类结果。
(4)不适合于发现非凸面形状的簇,或者大小差别很大的簇。
(5)对于"噪声"和孤立点数据敏感,少量的该类数据能够对平均值产生极大影响。
推荐系统
协同滤波(Collaborative Filtering, CF)是推荐系统中常用的一种方法,它主要基于用户之间或物品之间的相似性来生成推荐。协同滤波的基本假设是,如果用户 A 在过去喜欢了某些物品,而用户 B 在不同的物品集上显示出与用户 A 相似的喜好,则用户 B 可能也会喜欢用户 A 喜欢的那些未评价的物品。
协同滤波通常分为两大类:用户基于的协同滤波(User-Based Collaborative Filtering)和物品基于的协同滤波(Item-Based Collaborative Filtering)。
用户基于的协同滤波:
-
相似性计算:首先计算用户之间的相似度,通常基于用户的评分历史,使用诸如皮尔逊相关系数、余弦相似性等度量方法。
-
找到邻居:对于一个给定的用户,找出与他最相似的其他用户(即“邻居”)。
-
生成推荐:根据这些邻居的评分和相似度,预测目标用户对未评分物品的可能喜好,并提出推荐。
物品基于的协同滤波:
-
相似性计算:计算物品之间的相似度,这同样通常基于所有用户对这些物品的评分。
-
找到相似物品:对于用户已评分的每个物品,找出与之最相似的其他物品。
-
生成推荐:基于用户的现有评分以及相应物品的相似物品,预测用户对未知物品的喜好度,并据此提出推荐。
优点与限制:
-
优点:
- 直观易懂,基于实际用户行为而非内容属性,因此可以跨越不同类型的物品推荐。
- 能够发现和推荐给用户意外的新内容,从而增加用户的满意度和探索性。
-
限制:
- 冷启动问题:对于新用户或新物品缺乏足够的评分数据,协同滤波方法可能难以生成有效推荐。
- 数据稀疏性:在用户-物品评分矩阵中,评分项通常是非常稀疏的,这可能影响推荐质量。
- 可扩展性:随着用户和物品数量的增长,计算相似度和生成推荐的计算成本会显著增加。
Apriori
Apriori是关联分析中比较早的一种方法,主要用来挖掘那些频繁项集合。其思想是:
1. 如果一个项目集合不是频繁集合,那么任何包含它的项目集合也一定不是频繁集合;
2. 如果一个项目集合是频繁集合,那么它的任何非空子集也是频繁集合;
Aprioir需要扫描项目表多遍,从一个项目开始扫描,舍去掉那些不是频繁的项目,得到的集合称为L,然后对L中的每个元素进行自组合,生成比上次扫描多一个项目的集合,该集合称为C,接着又扫描去掉那些非频繁的项目,重复…
假设我们有以下交易记录,每个交易记录包含一些商品(项目):
- 交易1: {面包, 牛奶}
- 交易2: {面包, 尿布, 啤酒}
- 交易3: {牛奶, 尿布, 啤酒, 可乐}
- 交易4: {面包, 牛奶, 尿布}
- 交易5: {面包, 牛奶, 尿布, 啤酒}
- 交易6: {牛奶, 啤酒}
设最小支持度阈值为50%(即项集需要在至少3个交易中出现才认为是频繁的)。
步骤 1: 生成1-项集合并计算支持度
首先,列出所有单个项目的集合(1-项集),并计算每个集合在所有交易中出现的频率(支持度):
- {面包}: 4/6
- {牛奶}: 5/6
- {尿布}: 4/6
- {啤酒}: 4/6
- {可乐}: 1/6
只有{可乐}的支持度低于50%,所以我们将其舍去。
步骤 2: 生成2-项集合并计算支持度
接下来,对剩下的频繁1-项集进行自组合,生成所有可能的2-项集:
- {面包, 牛奶}: 3/6
- {面包, 尿布}: 3/6
- {面包, 啤酒}: 2/6
- {牛奶, 尿布}: 3/6
- {牛奶, 啤酒}: 3/6
- {尿布, 啤酒}: 3/6
在这里,{面包, 啤酒}的支持度低于50%,因此被舍去。
步骤 3: 生成3-项集合并计算支持度
然后,我们用剩下的频繁2-项集生成3-项集,并计算它们的支持度:
- {面包, 牛奶, 尿布}: 2/6
- {面包, 牛奶, 啤酒}: 1/6
- {面包, 尿布, 啤酒}: 1/6
- {牛奶, 尿布, 啤酒}: 2/6
所有这些3-项集的支持度都低于50%,因此它们都被舍去。
结果
最终,我们发现频繁项集为:
- 频繁1-项集:{面包}, {牛奶}, {尿布}, {啤酒}
- 频繁2-项集:{面包, 牛奶}, {面包, 尿布}, {牛奶, 尿布}, {牛奶, 啤酒}, {尿布, 啤酒}
没有频繁的3-项集。
通过Apriori算法,我们不仅发现了频繁出现的单个项目,还发现了经常一起出现的项目组合。这对于如超市货架布局、交叉销售策略等方面的决策制定是非常有用的。
随机森林
随机森林的工作原理包括以下几个步骤:
-
自助采样(Bootstrapping):对原始数据集进行多次重采样以生成多个不同的训练数据集。每次采样都是随机的,并允许重复选择同一数据点(即每个训练集可能包含重复的数据点,而一些原始数据点可能被遗漏)。
-
构建决策树:对每个新的训练数据集,构建一个决策树。在构建这些树的过程中,每次分割时选择最佳属性的过程中引入随机性:通常是从随机选取的属性子集中选择最佳属性,而不是考虑所有可能的属性。这增加了森林的多样性。
-
预测和决策:
- 分类任务:森林中的每棵树对样本进行分类,最后通过“多数投票”来确定最终类别。即,被森林中大多数树选中的类别成为最终预测结果。
- 回归任务:每棵树都会给出一个预测结果,最终输出的是所有树预测结果的平均值。
假设我们有一个小数据集,目标是根据天气条件预测是否适合进行野餐。
示例数据集:
假设我们的数据集如下,包含四个特征:温度、天气、风速和湿度,以及一个标签:是否野餐。
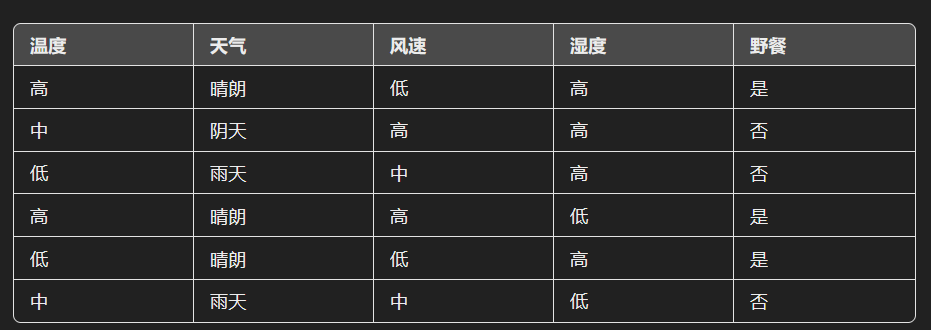
步骤 1: 自助采样
对原始数据进行自助采样(Bootstrap sampling),生成多个训练子集。假设我们生成了3个这样的子集:
- 子集1: {第1, 1, 3, 5行}
- 子集2: {第1, 2, 3, 4行}
- 子集3: {第2, 3, 5, 6行}
步骤 2: 构建决策树
对于每个子集,我们构建一个决策树。在每次分割时,我们不是查看所有特征,而是随机选择一部分特征。假设我们每次只选择两个特征来考虑。
- 对于子集1,假设随机选中的特征是“温度”和“风速”,然后基于这些特征构建决策树。
- 对于子集2,假设随机选中的特征是“天气”和“湿度”,然后构建决策树。
- 对于子集3,假设随机选中的特征是“天气”和“风速”,然后构建决策树。
步骤 3: 进行预测和汇总结果
当需要对新的数据点进行分类时(假设是:“温度=低,天气=晴朗,风速=高,湿度=低”),每棵树都会独立做出预测:
- 树1可能会根据“温度”和“风速”预测“是”(适合野餐)。
- 树2可能会根据“天气”和“湿度”预测“否”(不适合野餐)。
- 树3可能会根据“天气”和“风速”预测“是”(适合野餐)。
最后,我们通过多数投票来确定最终的分类结果。在这个例子中,因为有两棵树预测“是”,一棵树预测“否”,最终结果是“是”(适合野餐)。
结论:
通过这个过程,随机森林算法结合了多个决策树的结果来改进整体预测的准确性。每棵树都是在不完全相同的数据上训练,并且在分割时考虑不同的特征子集,这有助于增加模型的多样性,减少过拟合,提高泛化能力。