目录

树的直径

题目：树的直径 （两种解法）

做法一： 

 做法二：

树的重心：

题目： 会议

 思路：

题目：医院设置 

思路：

---

        

        

树的直径

定义：树中距离最远的两个点之间的距离被称为树的直径。

一共有两种做法，先记结论，再给证明！ 

做法一：

（1）任取一点作为起点x，找到距离该点最远的一个点y；

（2）再找到距离y最远的一点z，那么y、z之间的路径就是一条直径。

做法二：

（1）距离直径上的一个点最远的点和次远的点一定是直径的两个顶点，所以我们只要能找到距离每一个点的最远距离和次远距离就能找到树的直径了。

做法一证明：核心是证明y一定是直径的一个端点。

使用反证法证明，假设xy是直径(x,y为直径上点)，uv为非直径(u,v为非直径上点)。存在如下两种情况。

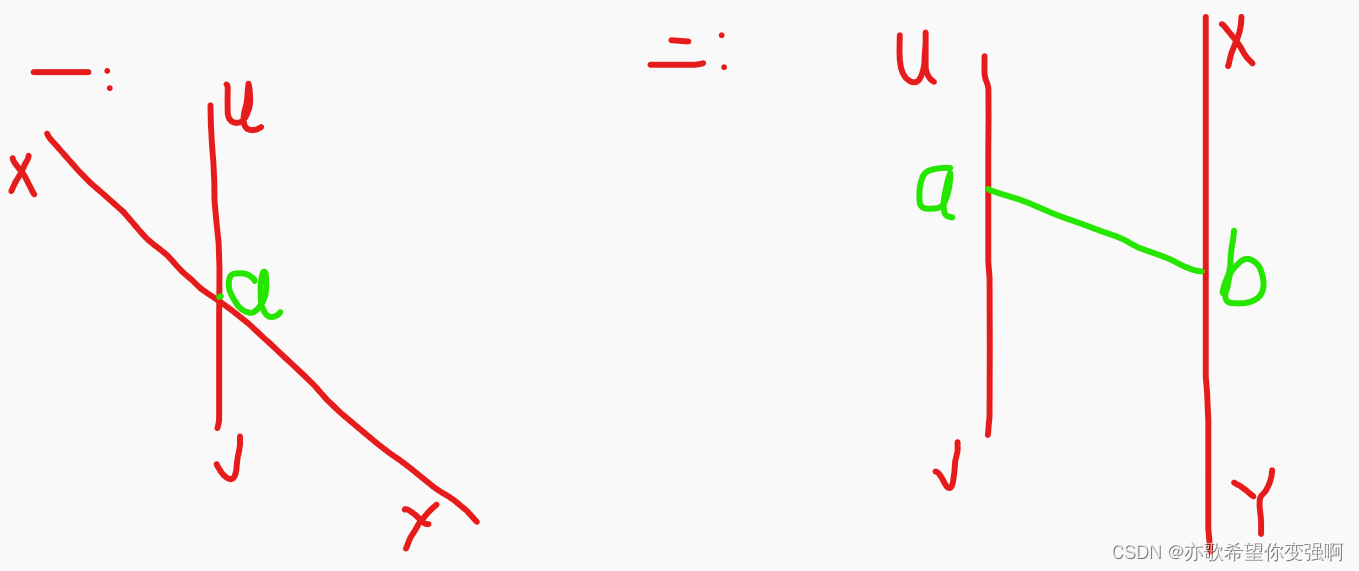
• 第一种情况是两者相交，故意假设v是距离u最远的点，有以下推论：

  ua+av>ua+ay    =>    av>ay    =>     av+ax>ay+ax=xy

  假设不成立，因v可以代表任意一个不是直径上的点，故距离u最远的点一定是直径上的点！

•  第二种情况是两者不相交，故意假设v是距离u最远的点，有以下推论：

  ua+av>ua+ab+by    =>    av > ab+by    =>    av+ab+bx>ab+by+ab+bx=2*ab+xy

  假设不成立，因v可以代表任意一个不是直径上的点，故距离u最远的点一定是直径上的点！

做法二证明：

前半句话不用……就不证明了吧，后半句“ 只要能找到距离每一个点的最远距离和次远距离就能找到树的直径了。” 意思就是把任意两点间的最长距离在某一点处砍成两半，当然有距离此点的最长距离和次长距离就是两头顶点间的最长距离，那么对所有点统计一下自然就找到直径长度了。

         

题目：树的直径 （两种解法）

spfa，dijkstra多用于跑有环的图，DAG图求最长距离直接dfs_dp就行！

做法一： 

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int tot,n,d[N],head[N];//d[i]表示到i点的距离
struct node{int to,w,nxt;}e[N*2];
void add(int u,int v,int w){e[++tot]=(node){v,w,head[u]};head[u]=tot;}void dfs(int u,int fa){for(int i=head[u];i;i=e[i].nxt){int v=e[i].to,w=e[i].w;if(v==fa)continue;d[v]=d[u]+w;//先更新再递归，因为d表示到u点的距离dfs(v,u);}
}
int main(){cin>>n;int u,v,w;for(int i=1;i<=n-1;i++){cin>>u>>v>>w;add(u,v,w);add(v,u,w);}dfs(1,0);//从任意点找最远距离的点int ans=-1;for(int i=1;i<=n;i++)if(d[i]>ans)ans=d[i],v=i;memset(d,0,sizeof(d));dfs(v,0);//此点必定在直径上，再跑一遍就完了for(int i=1;i<=n;i++)if(d[i]>ans)ans=d[i];cout<<ans;
}

 做法二：

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int ans=-1,tot,n,head[N];//d[i]表示到i点的距离
struct node{int to,w,nxt;}e[N*2];
void add(int u,int v,int w){e[++tot]=(node){v,w,head[u]};head[u]=tot;}int dfs(int u,int fa){int d1=0,d2=0;//d1是最长距离，d2是次长距离for(int i=head[u];i;i=e[i].nxt){int v=e[i].to,w=e[i].w;if(v==fa)continue;int d3=dfs(v,u)+w;//先更新距离if(d3>=d1) d2=d1,d1=d3;//如果是更长距离，最长和次长都更新else if(d3>d2)d2=d3;//如果仅比次长距离大，就仅更新次长距离}ans=max(ans,d1+d2);//最长距离加次长距离就是总长度return d1;//返回最长距离
}
int main(){cin>>n;int u,v,w;for(int i=1;i<=n-1;i++){cin>>u>>v>>w;add(u,v,w);add(v,u,w);}dfs(1,0);//从任意点开始cout<<ans;}

         

        

树的重心：

题目： 会议

         

 思路：

首先，阅读题目可以看出来，这道题目实际上就是求树的重心。

树的重心：

定义：找到一个点，其所有的子树中最大的子树节点数最少，那么这个点就是这棵树的重心，删去重心后，达到的效果是生成的多棵树尽可能平衡。

举个例子：

我们不妨设置d[i]表示以此点为根的所有点总距离和，cnt[i]表示以此为根的节点数

我们首先知道d[1]=16,cnt[1]=10我们来看d[2]应该怎么求,我们发现相对于d[1]来说，如果设2为最佳点,2,5,6其距离-1，剩下的1,4,3,7,8,9,10到其距离+1。

故：d[2]=d[1] - 3 + 7 =20

其中3是子根2对应的节点数cnt[2]，7是1为子根对应的节点数cnt[1]-cnt[2]

得：d[i]=d[fa]-cnt[i]+(cnt[1]-cnt[i])

那么只需要先dfs求出来d[1]和每个点的cnt[i]。然后就可以进行dp最终求出所有点的d[i]。

#include <bits/stdc++.h>
using namespace std;
const int N=50005;
int minn=0x3f3f3f3f,ans,n,d[N],cnt[N];
vector<int>ve[N];
void dfs(int u,int fa,int len){//一定别走fa回去cnt[u]++;//先加上自己for(int i=0;i<ve[u].size();i++){int v=ve[u][i];if(v==fa)continue;dfs(v,u,len+1);//先求孩子的cnt，之后求自己cntcnt[u]+=cnt[v];}d[1]+=len;//最后求d[1]
}
void dp(int u,int fa){for(int i=0;i<ve[u].size();i++){int v=ve[u][i];if(v==fa)continue;d[v]=d[u]-2*cnt[v]+cnt[1];dp(v,u);//这里对自己进行转移更新，再对孩子的更新}
}
int main(){cin>>n;int a,b;for(int i=1;i<n;i++){cin>>a>>b;ve[a].push_back(b);ve[b].push_back(a);}dfs(1,0,0);dp(1,0);for(int i=1;i<=n;i++){if(d[i]<minn)minn=d[i],ans=i;}cout<<ans<<" "<<minn;
}

上面我打注释的地方一定要理解 

        

        

题目：医院设置 

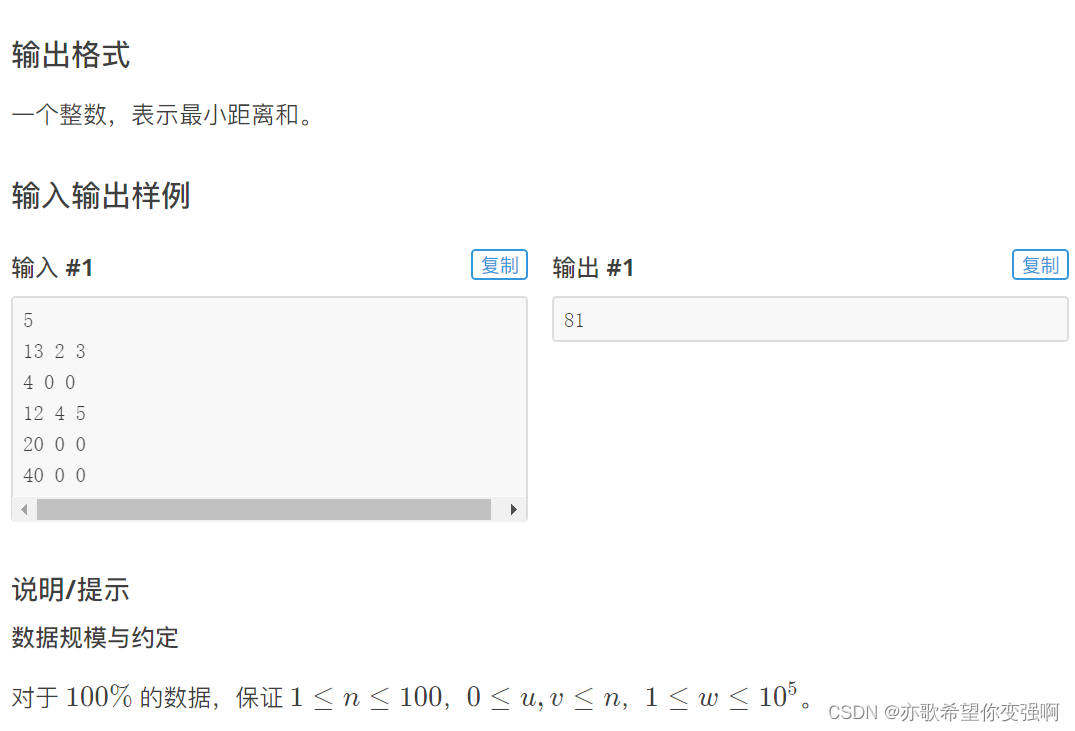
思路：

还是一道求树的重心题。不过是每个点都有一个权值。那么把权值当成“另一个世界的节点数”就好了。然后不断求cnt，之后dp就行。 

#include <bits/stdc++.h>
using namespace std;
const int N=500;
int ans=0x3f3f3f3f,n,d[N],cnt[N],w[N];
vector<int>ve[N];
void dfs(int u,int fa,int len){cnt[u]=w[u];//这里还是先加自己for(int i=0;i<ve[u].size();i++){int v=ve[u][i];if(v==fa)continue;dfs(v,u,len+1);cnt[u]+=cnt[v];}d[1]+=len*w[u];//更新d[1]也要变一下
}
void dp(int u,int fa){for(int i=0;i<ve[u].size();i++){int v=ve[u][i];if(v==fa)continue;d[v]=d[u]+cnt[1]-cnt[v]*2;dp(v,u);}ans=min(ans,d[u]);
}
int main(){cin>>n;int c,a,b;for(int i=1;i<=n;i++){cin>>c>>a>>b;w[i]=c;//注意输入方式if(a)ve[i].push_back(a),ve[a].push_back(i);if(b)ve[i].push_back(b),ve[b].push_back(i);}dfs(1,0,0);dp(1,0);cout<<ans;
}