wy的leetcode刷题记录_Day93

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉!
时间：2024-3-23

前言

2549. 统计桌面上的不同数字

今天的每日一题是：2549. 统计桌面上的不同数字

题目介绍

给你一个正整数 n ，开始时，它放在桌面上。在 109 天内，每天都要执行下述步骤：

• 对于出现在桌面上的每个数字 x ，找出符合 1 <= i <= n 且满足 x % i == 1 的所有数字 i 。
• 然后，将这些数字放在桌面上。

返回在 109 天之后，出现在桌面上的 不同 整数的数目。

注意：

• 一旦数字放在桌面上，则会一直保留直到结束。
• % 表示取余运算。例如，14 % 3 等于 2 。

示例 1：

输入：n = 5
输出：4
解释：最开始，5 在桌面上。 第二天，2 和 4 也出现在桌面上，因为 5 % 2 == 1 且 5 % 4 == 1 。 再过一天 3 也出现在桌面上，因为 4 % 3 == 1 。 在十亿天结束时，桌面上的不同数字有 2 、3 、4 、5 。

示例 2：

输入：n = 3
输出：2
解释： 因为 3 % 2 == 1 ，2 也出现在桌面上。 在十亿天结束时，桌面上的不同数字只有两个：2 和 3 。

思路

方法一：模拟，这里我只说思路，可以使用一个队列来存放需要求余的数。一开始队列里是n，根据n求出的数得到符合条件的数在入队，直到没有符合题意的数也就是队列空即可。
方法二：emmmmmmm，有木有发现n%n-1=1，其实每个数都会出现在桌子上，考虑1的特殊情况即可。这道题如果让我们判断某个数字出现的天数还是比较麻烦的，判断数字的个数其实仔细看看就一行代码就解决了。

代码

class Solution {
public:int distinctIntegers(int n) {return max(n-1,1);}
};

收获

无

827. 最大人工岛

827. 最大人工岛

题目介绍

给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。

返回执行此操作后，grid 中最大的岛屿面积是多少？

岛屿 由一组上、下、左、右四个方向相连的 1 形成。

示例 1:

输入: grid = [[1, 0], [0, 1]]
输出: 3
解释: 将一格0变成1，最终连通两个小岛得到面积为 3 的岛屿。

示例2:

输入: grid = [[1, 1], [1, 0]]
输出: 4
解释: 将一格0变成1，岛屿的面积扩大为 4。

示例 3:

输入: grid = [[1, 1], [1, 1]]
输出: 4
解释: 没有0可以让我们变成1，面积依然为 4。

思路

总体思路就是网格化dfs，进行两次dfs，一次用来计算各个岛屿的面积，并且给与编号来标记。第二次遍历海洋判断是否能与两边的陆地进行连接，维护连接后的最大面积。

代码

class Solution {
public:unordered_map<int, int> area; //每个区域面积int area_num = 0;void dfs(vector<vector<int>>& grid, int label, int x, int y){if(!(x>=0&& x< grid.size() && y>=0 && y< grid[0].size()))return;if(grid[x][y] == label || grid[x][y] == 0)return;area_num += 1;grid[x][y] = label;dfs(grid, label, x+1, y);dfs(grid, label, x-1, y);dfs(grid, label, x, y+1);dfs(grid, label, x, y-1);}int largestIsland(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();int label = 2;int ret = 0;for(int i=0; i< m; i++){for(int j=0; j< n; j++){if(grid[i][j] == 1){dfs(grid, label, i, j);area[label++] = area_num;ret = max(ret, area_num);area_num = 0;}}}vector<vector<int>> D = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};for(int i=0; i< m; i++){for(int j=0; j< n; j++){if(grid[i][j] == 0){int cur_area = 1;unordered_set<int> s;for(auto& d: D){int x = i+d[0];int y = j+d[1];if((x>=0&& x< grid.size() && y>=0 && y< grid[0].size())){if(grid[x][y]){s.insert(grid[x][y]);}}}for(auto i: s){cur_area += area[i];}ret = max(cur_area, ret);}}}return ret;}
};

收获

无

200. 岛屿数量

200. 岛屿数量

题目介绍

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid =
[ [“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”] ]
输出：1

示例 2：

输入：grid =
[ [“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”] ]
输出：3

思路

使用DFS遍历所有格子，将遍历过的格子进行标记即可，每当超过边界或者遇到海水或者遍历过的格子结束此次dfs搜寻，最后维护岛屿个数变量。

代码

class Solution {
public:void dfs(vector<vector<char>>& grid,int x,int y){if(x<0||x>=grid.size()||y<0||y>=grid[0].size())return ;if(grid[x][y]!='1')return ;grid[x][y]='0';dfs(grid,x+1,y);dfs(grid,x,y+1);dfs(grid,x,y-1);dfs(grid,x-1,y);}int numIslands(vector<vector<char>>& grid) {int ans=0;int n=grid.size();int m=grid[0].size();for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(grid[i][j]=='1'){                dfs(grid,i,j);ans++;}}}return ans;}
};

收获

无

463. 岛屿的周长

463. 岛屿的周长

题目介绍

给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地， grid[i][j] = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

示例 1：

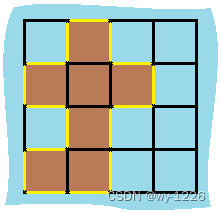
输入：grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出：16
解释：它的周长是上面图片中的 16 个黄色的边

示例 2：

输入：grid = [[1]]
输出：4

示例 3：

输入：grid = [[1,0]]
输出：4

思路

仔细观察题，其实这道题可以理解为判断贡献度的问题，当你通过dfs遍历到一个陆地时，如果你的临近的某一块格子是水或者是边界，那么你当前所处的陆地就存在这一条临近边，如果你的临近的格子是一块陆地的话，那么就没有这条临近边，一共四个方向判断。

代码

DFS：

class Solution {
public:int dfs(vector<vector<int>> & grid,int x,int y){if(x>=grid.size()||x<0||y>=grid[0].size()||y<0||grid[x][y]==0){return 1;}if(grid[x][y]==2)return 0;grid[x][y]=2;return dfs(grid,x+1,y)+dfs(grid,x,y+1)+dfs(grid,x-1,y)+dfs(grid,x,y-1);}int islandPerimeter(vector<vector<int>>& grid) {int n=grid.size();int m=grid[0].size();int ans=0;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(grid[i][j]==1)ans+=dfs(grid,i,j);}}return ans;}
};

遍历：

class Solution {
public:int islandPerimeter(vector<vector<int>>& grid) {int n=grid.size();int m=grid[0].size();int ans=0;for(int i=0;i<n;i++){for(int j=0;j<m;j++){int count=0;if(grid[i][j]==1){if(i+1>=n||grid[i+1][j]!=1)count++;if(i-1<0||grid[i-1][j]!=1)count++;if(j+1>=m||grid[i][j+1]!=1)count++;if(j-1<0||grid[i][j-1]!=1)count++;}ans+=count;}}return ans;}
};

收获

本次了解了网格化的dfs的一些操作流程，以及特殊情况的记录。