GAMES101 作业0

1.向量点积

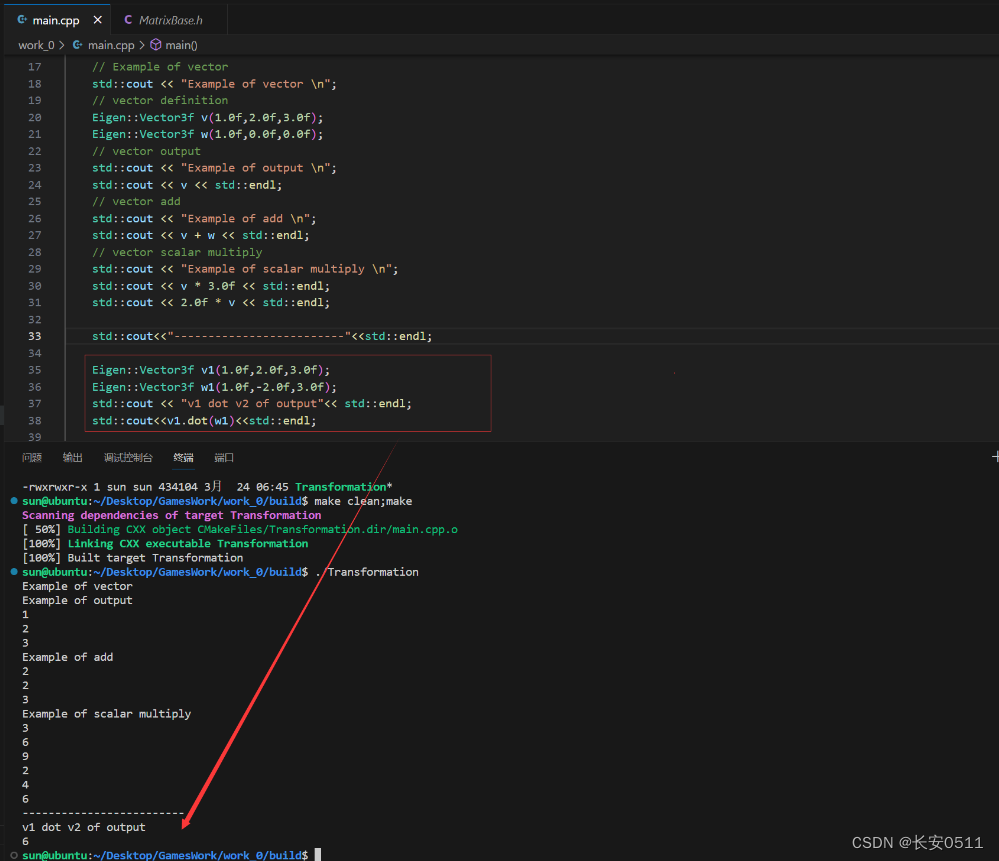
在这里插入图片描述

dot(a, b) = a1 * b1 + a2 * b2 + ... + an * bn

根据sample，我们可以通过dot进行向量点积

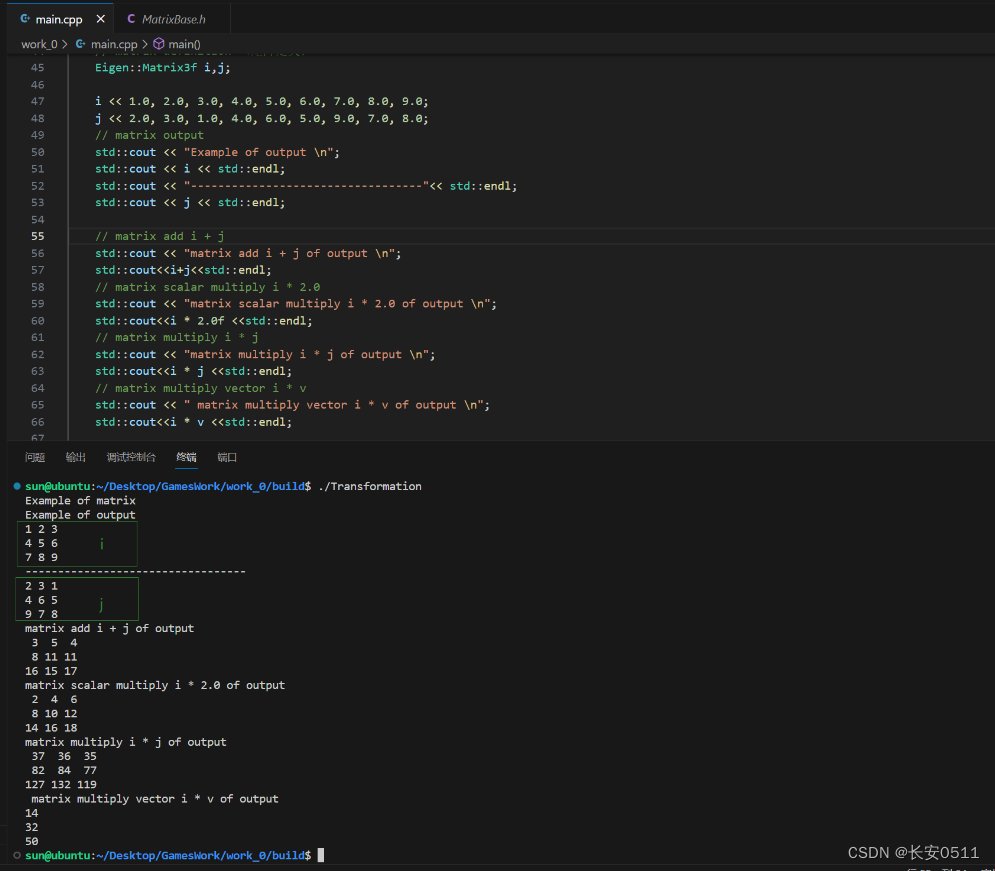
2.矩阵运算

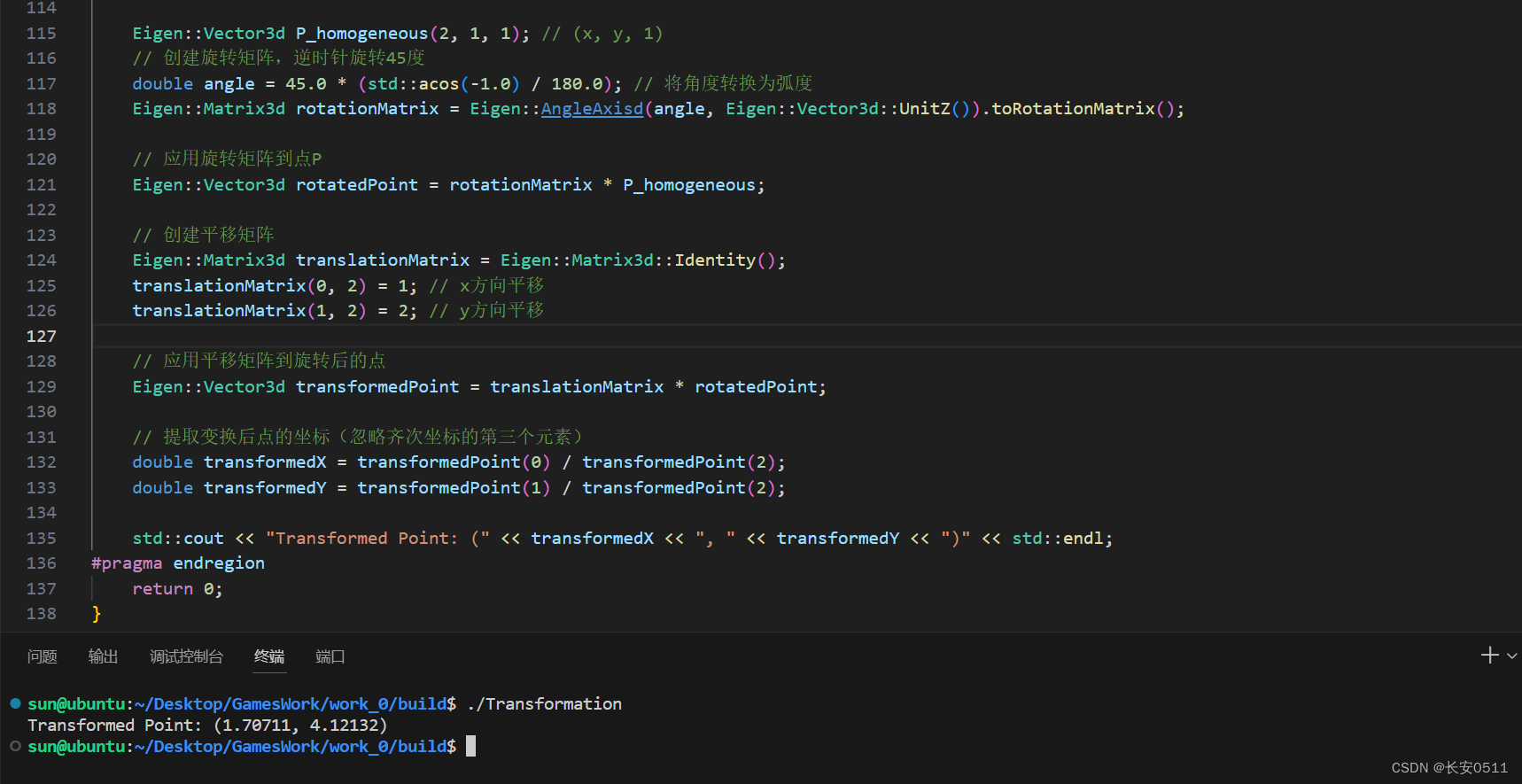
在这里插入图片描述

3.给定一个点 P=(2,1), 将该点绕原点先逆时针旋转 45◦，再平移 (1,2), 计算出变换后点的坐标（要求用齐次坐标进行计算）。

方式1

Eigen::Vector3f p(2.0f, 1.0f, 1.0f);Eigen::Matrix3f R, M;// Convert angle to radiansfloat angle = 45.0f * M_PI / 180.0f;// Rotation matrixR << std::cos(angle), -std::sin(angle), 0.0f,std::sin(angle), std::cos(angle), 0.0f,0.0f, 0.0f, 1.0f;// Translation matrixM << 1.0f, 0.0f, 1.0f,0.0f, 1.0f, 2.0f,0.0f, 0.0f, 1.0f;// Apply rotation and translationEigen::Vector3f ans = M * R * p;std::cout <<"transformedX = "<< ans(0) << std::endl;std::cout <<"transformedY = "<< ans(1) << std::endl;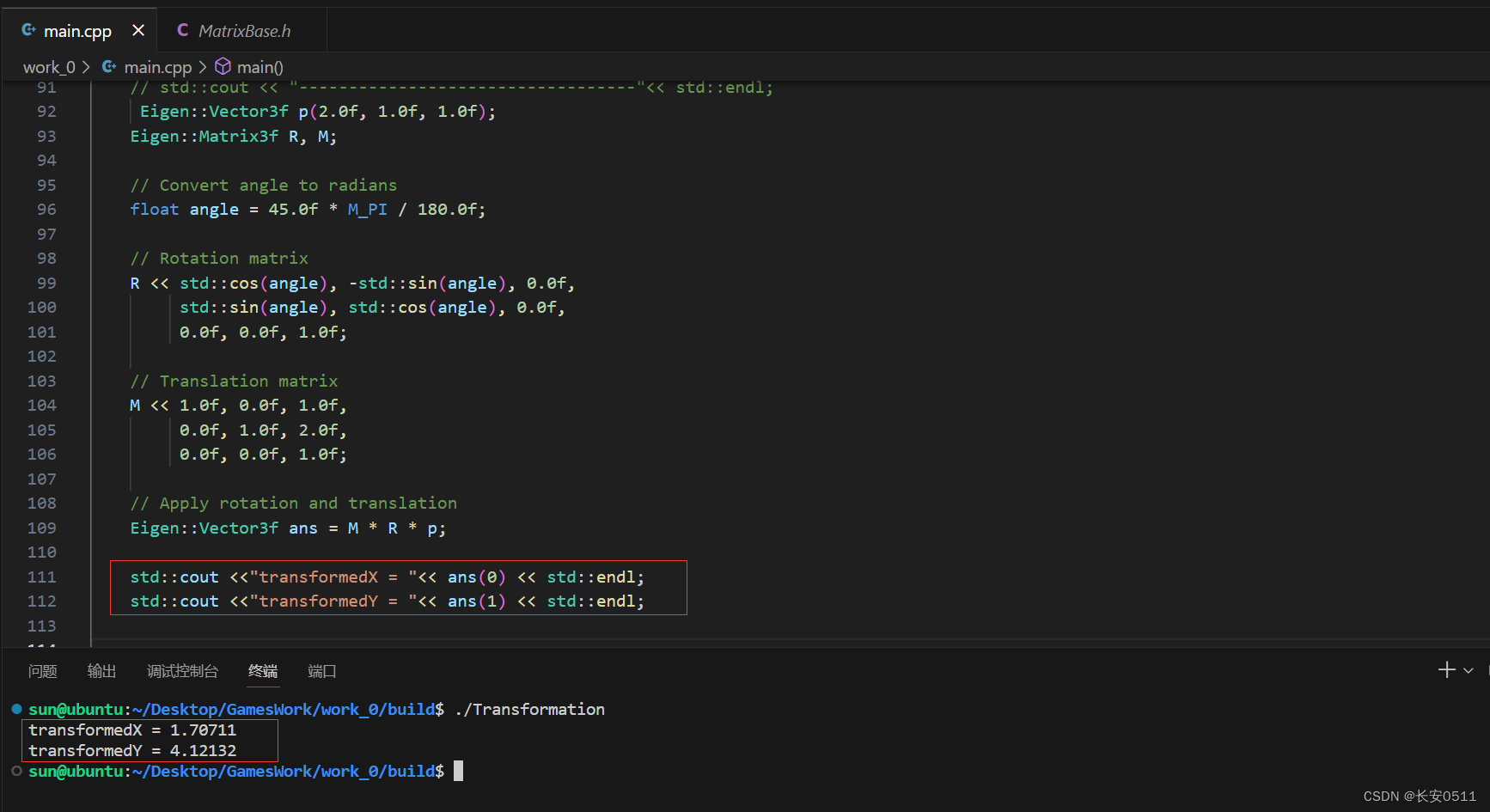

在这里插入图片描述

方式2

 Eigen::Vector3d P_homogeneous(2, 1, 1); // (x, y, 1)// 创建旋转矩阵，逆时针旋转45度  double angle = 45.0 * (std::acos(-1.0) / 180.0); // 将角度转换为弧度  Eigen::Matrix3d rotationMatrix = Eigen::AngleAxisd(angle, Eigen::Vector3d::UnitZ()).toRotationMatrix();  // 应用旋转矩阵到点P  Eigen::Vector3d rotatedPoint = rotationMatrix * P_homogeneous;  // 创建平移矩阵  Eigen::Matrix3d translationMatrix = Eigen::Matrix3d::Identity();  translationMatrix(0, 2) = 1; // x方向平移  translationMatrix(1, 2) = 2; // y方向平移  // 应用平移矩阵到旋转后的点  Eigen::Vector3d transformedPoint = translationMatrix * rotatedPoint;  // 提取变换后点的坐标（忽略齐次坐标的第三个元素）  double transformedX = transformedPoint(0) / transformedPoint(2);  double transformedY = transformedPoint(1) / transformedPoint(2);  std::cout << "Transformed Point: (" << transformedX << ", " << transformedY << ")" << std::endl;