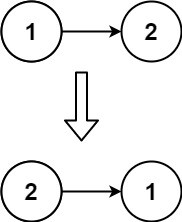
在多层感知器被引入的同时,也引入了一个新的问题:由于隐藏层的预期输出并没有在训练样例中给出,隐藏层结点的误差无法像单层感知器那样直接计算得到。
为了解决这个问题,反向传播(BP)算法被引入,其核心思想是将误差由输出层向前层反向传播,利用后一层的误差来估计前一层的误差。
反向传播算法由亨利·J.凯莉在1960年首先提出,阿瑟·E.布赖森也在1961年进一步讨论该算法。
使用反向传播算法训练的网络称为BP网络。
一、梯度下降
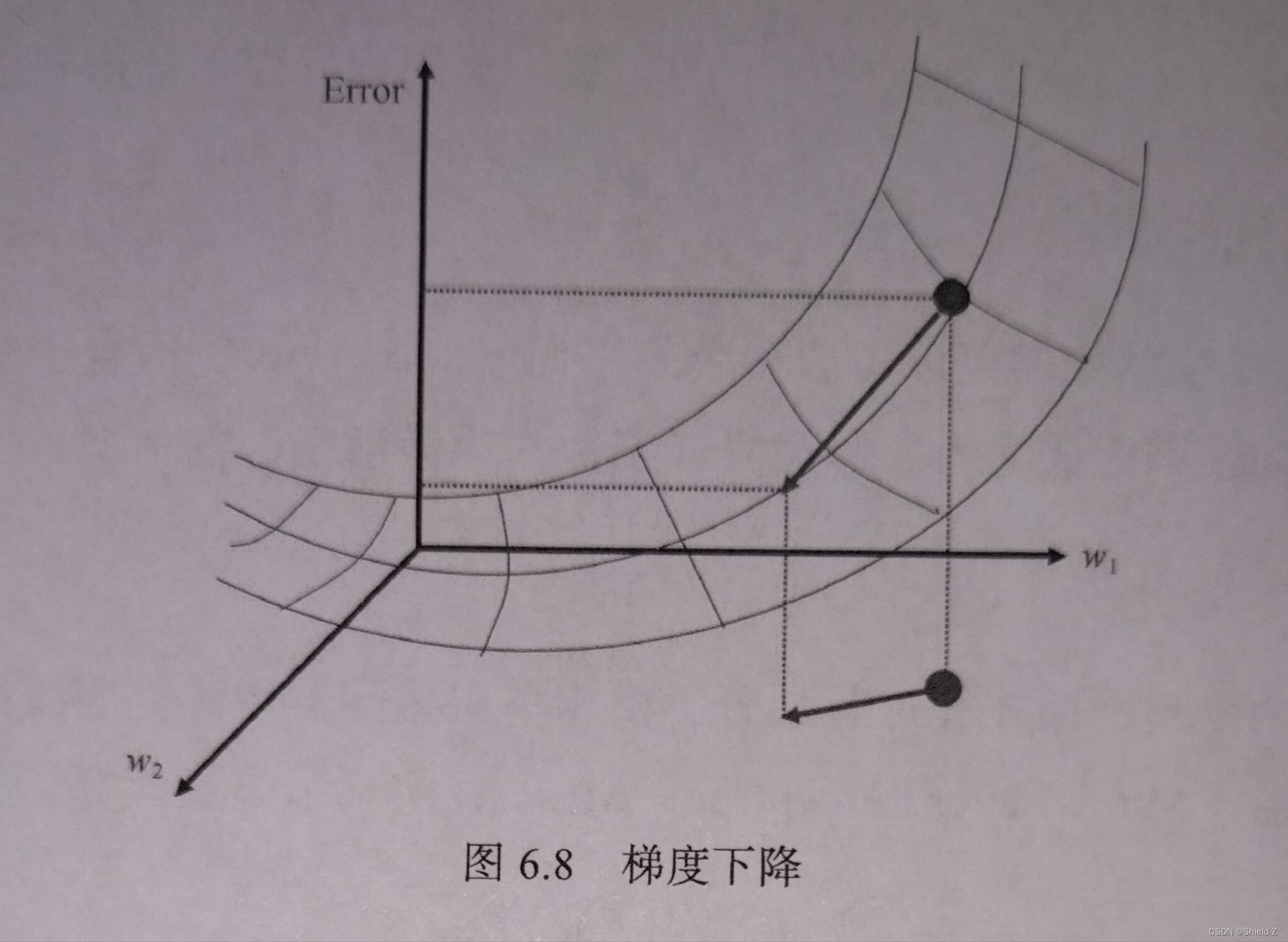
为了使得误差可以反向传播,梯度下降的算法被采用,其思想是在权值空间中朝着误差下降最快的反向搜索,找到局部的最小值:
w ← w + △w
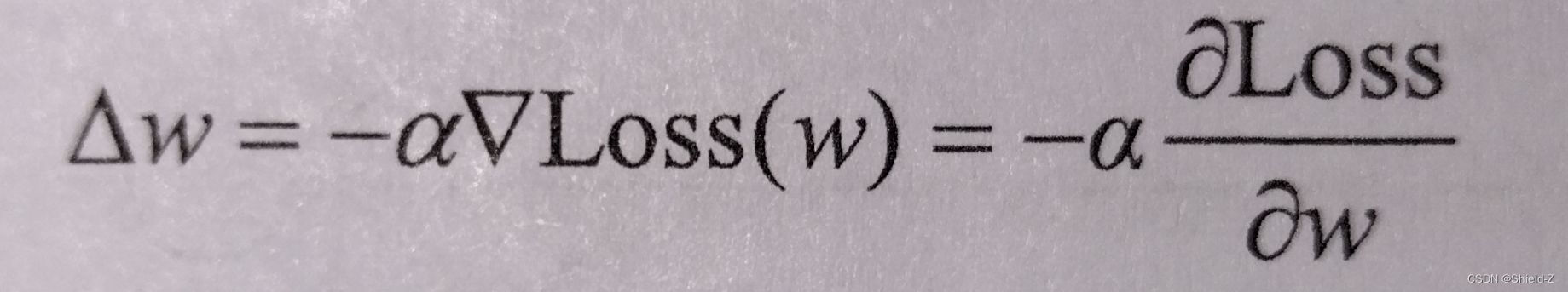
其中,w 为权值,α为学习率,Loss(·)为损失函数。
损失函数的作用是计算实际输出与期望输出之间的误差。
常用的损失函数如下:
1、均方误差,实际输出为oi,预期输出为yi :

2、交叉熵(CE):
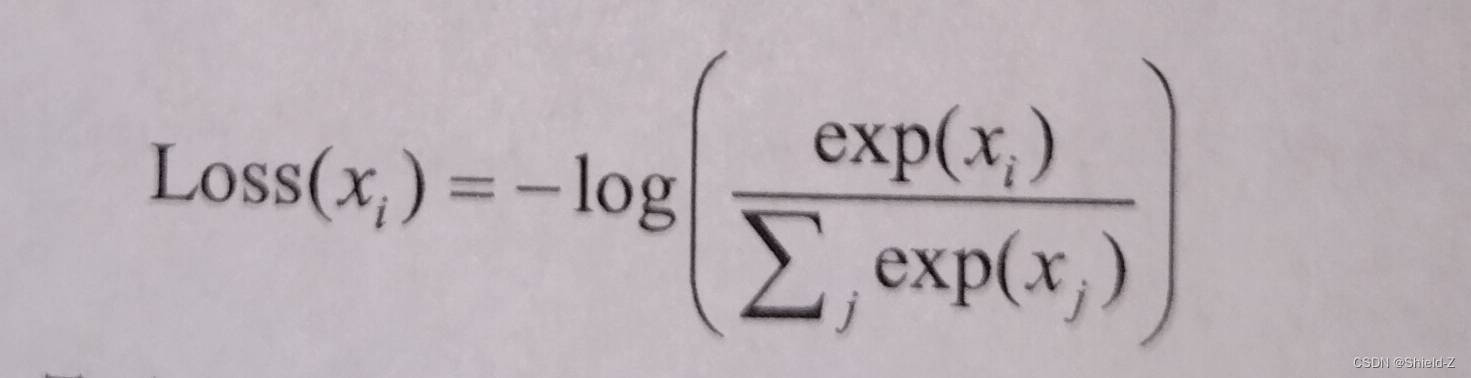
由于求偏导需要激活函数是连续的,而符号函数不满足连续的要求,因此通常使用连续可微的函数,如sigmoid作为激活函数。
特别的,sigmoid具有良好的求导性质:
σ ' = σ(1 - σ)
sigmoid函数使得计算偏导时较为方便,因此被广泛应用。
二、反向传播
使得误差反向传播的关键在于利用求偏导的链式法则。
我们知道,神经网络是直观展示的一系列计算操作,每个节点可以用一个函数 f (·) 来表示。
下图所示的神经网络则可以表达一个以 w₁,...,w₆ 为参量,以 i₁,...,i₄ 为变量的函数:
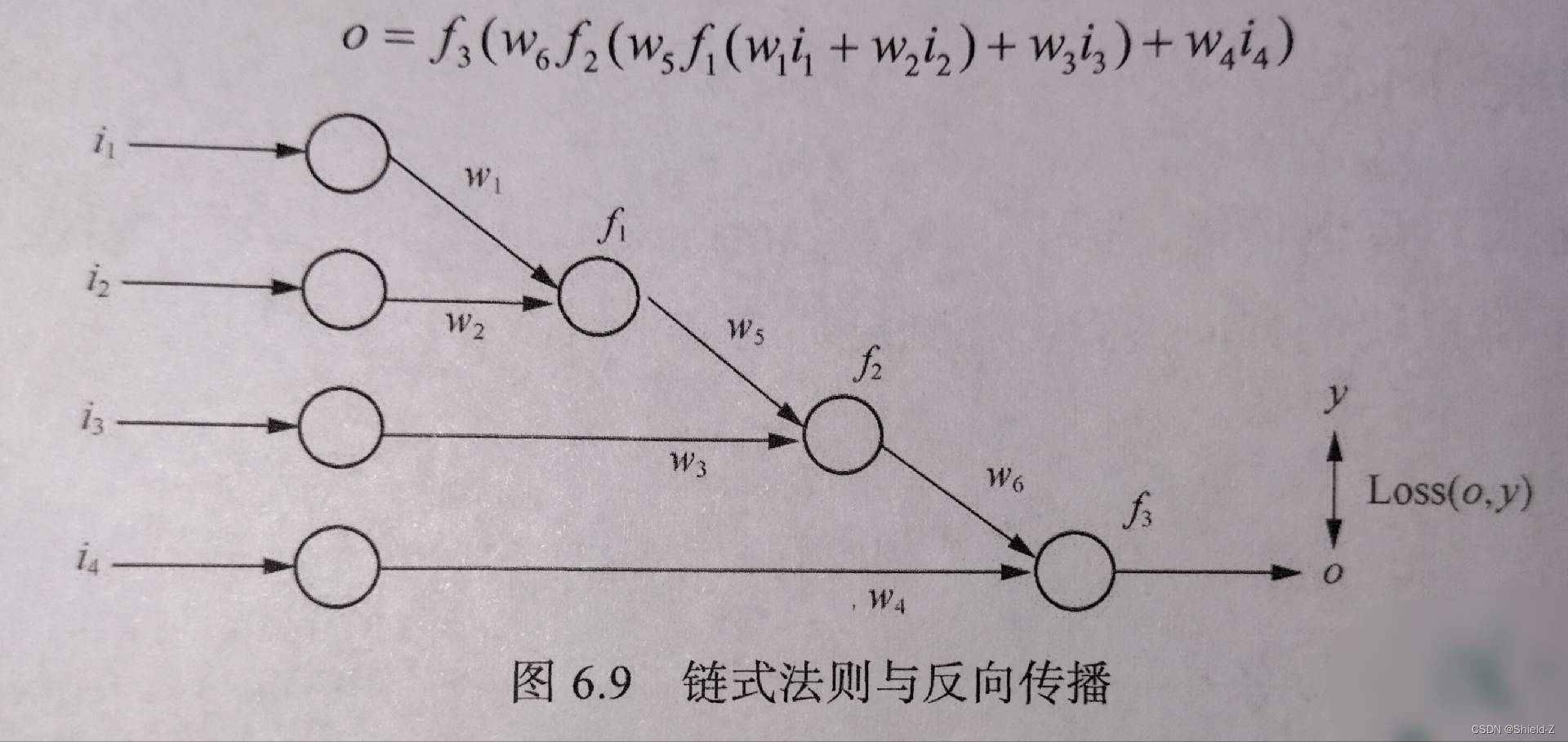
在梯度下降中,为了求 △Wk,我们需要用链式规则去求 ,
,
例如求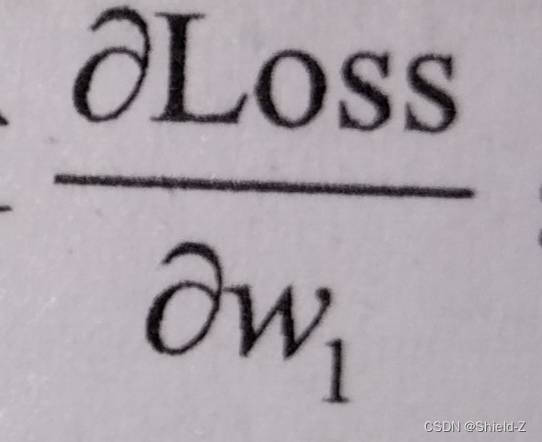 :
:
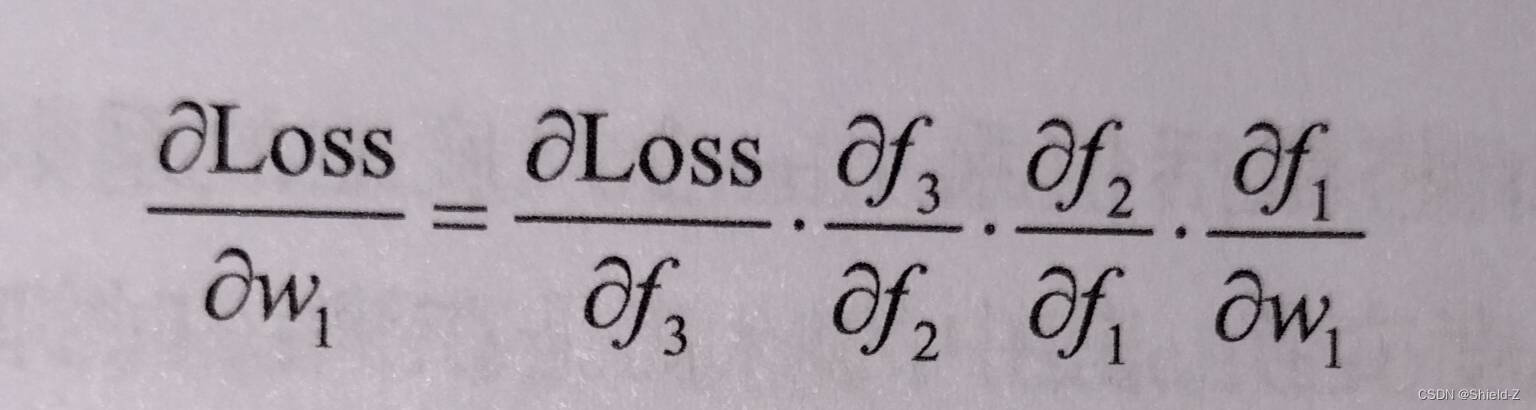
通过这种方式,误差得以反向传播并用于更新每一个连续权值,使得神经网络在整体上逼近损失函数的局部最小值,从而达到训练目的。