文献阅读

1. 题目

标题：Generative Adversarial Networks

作者：Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio

期刊名：Communications of the ACM

链接：arXiv:1406.2661

2. abstract

该文提出了名为对抗性生成模型的新框架。该框架同时训练两个模型：生成模型G提取数据分布特征，判别模型D分辨输入数据来自训练数据还是由G生成。G的训练过程时最大限度的提高D出错的概率。在文中实验通过对生成样本进行定性和定量评估，展示了该框架的潜力。

This article proposes a new framework for estimating generative models via an adversarial process. This framework includes two model: a generative model G that captures the data distribution, and a discriminative model D that estimates the probability that a sample came from the training data rather than G. Experiments demonstrate the potential of the framework through qualitative and quantitative evaluation of the generated samples in this article.

3. 网络架构

为了学习生成器在数据x上的分布$p_g$，定义输入噪声变量$p_{\mathbf{z}}(\mathbf{z})$的先验概率，然后将到数据空间的映射表示为$G(\mathbf{z};{\theta }_g)$，其中G是由多层感知器表示的可微函数，该函数的参数为${\theta }_g$。此外，定义了输出单个标量的第二个多层感知器$D(\mathbf{x};{\theta }_d)$。 D(x)表示x来自数据而不是$p_g$的概率。以最大化训练数据和G生成样本分配正确标签的概率为目标训练D。同时训练G以最小化$\text{log}(1-D(G(\mathbf{z})))$。从而有如下损失函数：
$${\text{min}}_G{\text{max}}_{D}V(D,G)={\mathbb{E}}_{x\sim p_{data}(\mathbf{x})}[\text{log}D(\mathbf{x})]+{\mathbb{E}}_{x\sim z_z(z)}[\text{log}(1-D(G(\mathbf{z})))]\text{\hspace{1em}(1)}$$

GAN训练时同步更新判别分布（D，蓝色虚线），从而区分数据分布$p_x$（黑色虚线）和生成数据分布$p_g(G)$的样本（绿色实线）。下面水平线是在本例中均匀分布的从z采样的域。上面水平线是x域的一部分。箭头表示$x=G(z)$在变换后样本上施加非均匀分布$p_g$。

若模型处于收敛状态，则$p_g$类似于$p_{data}$，此时D分类准确。D收敛时有$D^{\ast }(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$。在更新G后，D更有可能将其分类为真实数据。若D和G有足够容量，则经过几次迭代后，将趋于收敛，此时$p_g=p_{data}$，辨别器无法区分二者，$D(x)=\frac{1}{2}$

单个迭代内的训练循环：D优化k次，G优化一次

式1可能无法为G提供足够的梯度。在训练的早期，当G很差时，D可以以高置信度拒绝样本，因为它们与训练数据明显不同。在这种情况下，$\log (1-D(G(z)))$饱和。此时，以$\text{argmax}\log D(G(z))$为目标，训练G。使用这种方式可以在训练早期提供更强的梯度。

3.1 Theoretical Results

生成器定义了一个概率分布$p_g$，该分布当$z\sim p_z$时得到样本$G(z)$。因此有设计目标：若有足够容量和训练时间，则下列算法收敛至好的$p_{data}$。下图解释了算法1以及上述的损失函数
在这里插入图片描述

上图即算法1

Global Optimality of $p_g=p_{data}$

命题1：对于固定G，最优辨别器D为
$$D_G^{\ast }=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}\text{\hspace{1em}(2)}$$
证明：对于任意生成器G，辨别器D的训练标准是最大化$V(G.D)$
$$\begin{array}{r}V(D,G)={\int }_x{p}_{data}(\mathbf{x})\text{log}D(\mathbf{x})\text{dx}+{\int }_x{p}_z(z)\text{log}(1-D(G(\mathbf{z})))\text{dz}\\ ={\int }_x{p}_{data}(\mathbf{x})\text{log}D(\mathbf{x})\text{dx}+p_x(z)\text{log}(1-D(G(\mathbf{z})))\text{dz}\end{array}\text{\hspace{1em}(3)}$$
对于任意 ( a , b ) ∈ R 2 \ { 0 , 0 } (a,b)\in \mathbb R^2\backslash \{0,0\} (a,b)∈R2\{0,0}，函数$y\to a\log (y)+b\log (1-y)$在$[0,1]$范围内达到其最大值$\frac{a}{a+b}$

首先给定 G 很容易计算出 D 存在一个最优解。而 $p_{data}$ 是一个概率，所以积分本质仍然在求期望。在第二项中做了一个换元 。那么原来$p_z(z)$也就是随机变量 z 的一个噪声的随机分布，就相应的被映射成了$p_g(x)$也就是生成的样例的分布。原来对 z 的积分，当然也就变成了对此处 x 的积分，注意积分的值与积分变量无关，所以x 并没有什么实际含义可以换成任意字母，换成 x 是为了与前面合并为一项。

从而有（3）式结尾的积分。若将$p_{data}(x)$和$p_g(x)$抽象为a、b，则有$a\cdot \log (y)+b\cdot \log (1-y)$，易得最大值$\frac{a}{a+b}$，即证明对于任意G总有最优D

D 的训练目标可以解释为最大化估计条件概率 $P(Y=y|\mathbf{x})$的对数似然，其中 Y 表示 x 是来自 $p_{data}(y=1)$还是来自 $p_g(y=0)$。方程 1 现在可以重新表述为

下图为定理1及其证明过程

证明 G 存在全局最优解。把刚才 D 的最优解直接带回损失函数，就得到了上面的（4）式。然后分母乘上一个二分之一，并对应的在log外面抵消掉二分之一，这个操作是为了让分数线下面的数值在 [0,1] 范围内，从而描述了 $p_{data}$ 与 $p_g$ 综合起来这样一个分布。从而得到了两个分布的KL散度，KL散度越小就说明分子两个分布越相似。KL散度越小，说明两个分布越相似，说明 G 学习真实分布学习的越好。这两个KL散度求平均，又是JSD散度，同理JSD散度越小说明两个分布越相似，也说明 G 学习真实分布学习的越好。

Convergence of Algorithm 1

4. 文献解读

4.1 Introduction

为了在生成式任务中充分利用ReLU的优点，该文提出了一种新的生成模型评估程序。辨别模型学习确定样本来自于训练数据以及生成模型的概率。生成模型学习训练数据的概率，从而生成在辨别模型结果中属于训练数据概率尽可能高的数据。在对抗性网络框架下，二者相互促进，直至辨别模型判别训练数据与生成数据的概率相近。文中主要探讨了两者均是多层感知器的情况。

4.2 创新点

1. 本文提出了新型框架——生成式对抗网络（GAN）
2. 对于该网络给出两个证明，分别证明
   1. 其生成器拟合的分布能够达到全局最优
   2. 其训练算法——上文中算法1，能够收敛

4.3 实验过程

4.3.1 数据集

使用一系列数据集训练对抗网络，包括MNIST[23]、Toronto Face Database(TFD)[28] 和 CIFAR-10[21]。

4.3.2 参数设置

生成器网络G使用两个激活函数：ReLU和 sigmoid的混合，而鉴别器网D络使用 maxout激活函数。 使用Dropout训练鉴别器网络。仅使用噪声作为生成器网络最底层的输入

通过将高斯Parzen窗口拟合到G生成的样本并报告该分布下的对数似然来估计 $p_g$ 下测试集数据的概率。高斯函数的$\sigma$参数是通过验证集上的交叉验证获得的。结果如下表所示。这种评估可能性的方法具有较高的方差，并且在高维空间中表现不佳，但是当时最佳方法。

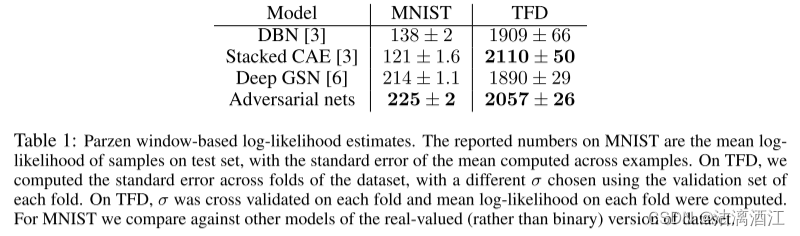
上表是基于 Parzen 窗口的对数似然估计。

MNIST上的数字是测试集上样本的平均对数似然，以及跨示例计算的平均值的标准误差。

TFD上，计算了数据集折叠的标准误差，并使用每个折叠的验证集选择不同的$\sigma$。在TFD上，对每个折叠的$\sigma$进行交叉验证，并计算每个折叠的平均对数似然。

对于MNIST，与数据集实值（而不是二进制）版本的其他模型进行比较。

下图展示了训练后从生成网络中抽取的样本

上图左上来自MNIIST、右上TFD、左下CIFAR-10（全连接模型）、右下CIFAR-10（卷积判别器和“反卷积”生成器）

4.4 结论

该模型填补了生成领域模型框架的空白，且证明了其实际可行性以及理论可行性。

缺点主要是没有$p_g(x)$的显式表示，并且训练时D必须与G很好地同步

优点是不需要马尔可夫链，仅使用反向传播来获取梯度，学习过程中不需要推理，并且可以将多种函数合并到模型中。

三、实现GAN

1. 任务要求

使用pytorch实现GAN网络，并使用MNIST数据库训练GAN，GAN绘制手写数字图片。其中，GAN使用MLP构建

2. 实验结果

GAN进行十九次迭代后的绘制效果

3.实验代码

3.1数据准备

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
import torchvision
from torchvision import transforms

# 数据准备# 对数据做归一化 （-1， 1）
transform = transforms.Compose([transforms.ToTensor(),         # 将数据转换成Tensor格式，channel, high, witch,数据在（0， 1）范围内transforms.Normalize(0.5, 0.5) # 通过均值和方差将数据归一化到（-1， 1）之间
])# 下载数据集
train_ds = torchvision.datasets.MNIST('data',train=True,transform=transform,download=True)# 设置dataloader
dataloader = torch.utils.data.DataLoader(train_ds, batch_size=64, shuffle=True)# 返回一个批次的数据
imgs, _ = next(iter(dataloader))# imgs的大小
imgs.shape

3.2 模型构建

# 定义生成器# 输入是长度为 100 的 噪声（正态分布随机数）
# 输出为（1， 28， 28）的图片
# linear 1 :   100----256
# linear 2:    256----512
# linear 2:    512----28*28
# reshape:     28*28----(1, 28, 28)class Generator(nn.Module): #创建的 Generator 类继承自 nn.Moduledef __init__(self): # 定义初始化方法super(Generator, self).__init__() #继承父类的属性self.main = nn.Sequential( #使用Sequential快速创建模型nn.Linear(100, 256),nn.ReLU(),nn.Linear(256, 512),nn.ReLU(),nn.Linear(512, 28*28),nn.Tanh()                     # 输出层使用Tanh()激活函数，使输出-1, 1之间)def forward(self, x):              # 定义前向传播 x 表示长度为100 的noise输入img = self.main(x)img = img.view(-1, 28, 28) #将img展平，转化成图片的形式，channel为1可写可不写return img# 定义判别器## 输入为（1， 28， 28）的图片  输出为二分类的概率值，输出使用sigmoid激活 0-1
# BCEloss计算交叉熵损失# nn.LeakyReLU   f(x) : x>0 输出 x， 如果x<0 ,输出 a*x  a表示一个很小的斜率，比如0.1
# 判别器中一般推荐使用 LeakyReLUclass Discriminator(nn.Module):def __init__(self):super(Discriminator, self).__init__()self.main = nn.Sequential(nn.Linear(28*28, 512), #输入是28*28的张量，也就是图片nn.LeakyReLU(), # 小于0的时候保存一部分梯度nn.Linear(512, 256),nn.LeakyReLU(),nn.Linear(256, 1), # 二分类问题，输出到1上nn.Sigmoid())def forward(self, x):x = x.view(-1, 28*28)x = self.main(x)return x

3.3 展示函数

# 绘图函数def gen_img_plot(model, epoch, test_input):prediction = np.squeeze(model(test_input).detach().cpu().numpy())fig = plt.figure(figsize=(4, 4))for i in range(16):plt.subplot(4, 4, i+1)plt.imshow((prediction[i] + 1)/2) # 确保prediction[i] + 1)/2输出的结果是在0-1之间plt.axis('off')plt.show()test_input = torch.randn(16, 100, device=device)

3.4 训练过程

# GAN的训练# 保存每个epoch所产生的loss值
D_loss = []
G_loss = []# 训练循环
for epoch in range(20): #训练20个epochd_epoch_loss = 0 # 初始损失值为0g_epoch_loss = 0# len(dataloader)返回批次数，len(dataset)返回样本数count = len(dataloader)# 对dataloader进行迭代for step, (img, _) in enumerate(dataloader): # enumerate加序号img = img.to(device) #将数据上传到设备size = img.size(0) # 获取每一个批次的大小random_noise = torch.randn(size, 100, device=device)  # 随机噪声的大小是size个d_optim.zero_grad() # 将判别器前面的梯度归0real_output = dis(img)      # 判别器输入真实的图片，real_output是对真实图片的预测结果 # 得到判别器在真实图像上的损失# 判别器对于真实的图片希望输出的全1的数组，将真实的输出与全1的数组进行比较d_real_loss = loss_fn(real_output, torch.ones_like(real_output))      d_real_loss.backward() # 求解梯度gen_img = gen(random_noise)    # 判别器输入生成的图片，fake_output是对生成图片的预测# 优化的目标是判别器，对于生成器的参数是不需要做优化的，需要进行梯度阶段，detach()会截断梯度，# 得到一个没有梯度的Tensor，这一点很关键fake_output = dis(gen_img.detach()) # 得到判别器在生成图像上的损失d_fake_loss = loss_fn(fake_output, torch.zeros_like(fake_output))      d_fake_loss.backward() # 求解梯度d_loss = d_real_loss + d_fake_loss # 判别器总的损失等于两个损失之和d_optim.step() # 进行优化g_optim.zero_grad() # 将生成器的所有梯度归0fake_output = dis(gen_img) # 将生成器的图片放到判别器中，此时不做截断，因为要优化生成器# 生层器希望生成的图片被判定为真g_loss = loss_fn(fake_output, torch.ones_like(fake_output))      # 生成器的损失g_loss.backward() # 计算梯度g_optim.step() # 优化# 将损失累加到定义的数组中，这个过程不需要计算梯度with torch.no_grad():d_epoch_loss += d_lossg_epoch_loss += g_loss# 计算每个epoch的平均loss，仍然使用这个上下文关联器with torch.no_grad():# 计算平均的loss值d_epoch_loss /= countg_epoch_loss /= count# 将平均loss放入到loss数组中D_loss.append(d_epoch_loss.item())G_loss.append(g_epoch_loss.item())# 打印当前的epochprint('Epoch:', epoch)# 调用绘图函数gen_img_plot(gen, epoch, test_input)

小结

本文主要讨论了生成式对抗神经网络。首先，本文介绍了生成式对抗网络的设计思路。在此基础下，本文阐述了GAN的网络结构以及训练过程。生成器与解释器相互迭代，随着更新，生成器的效果趋近于真实图片。其次，本文展示了题为Generative Adversarial Networks论文的主要内容。这篇论文提出了生成式对抗网络的网络结构以及训练过程，该模型填补了生成任务方面神经网络的空白。此外，这篇论文还从理论角度证明了生成器的数据分布能够达到全局最优以及训练算法的可收敛性。最后，本文基于pytorch以及MNIST数据集实现了GAN绘制手写数字。

本周内容简报

之前学习的神经网络以特征值x为输入，GAN除了x以外还能将简单的数据分布作为输入。

设计者可以将GAN当作游戏手柄，以指令控制神经网络，这提升了神经网络的可操作性。

随后是GAN的训练过程，首先固定生成器、更新解释器，解释器将更能识破生成器的伪装。越接近真实数据分布的样本，在解释器的得分越高。其次固定解释器、更新生成器，生成器更能逃过解释器的识别。从而生成器的数据分布也越接近真实数据。将两步迭代进行便是GAN的训练过程。

此外，本周阅读的论文中还提出了k step的概念，即更新k步D然后更新一步G。

下周计划

继续学习GAN模型以及阅读相关论文，实现较为复杂的GAN网络，可能考虑HW6。

参考文献

[1] Goodfellow, Ian J., et al. “Generative Adversarial Networks.” arXiv.Org, 10 June 2014, arxiv.org/abs/1406.2661.