一.数据平稳性与差分法
1.平稳性:


2.差分法:
错开时间点,使得数据可以平稳

原数据➡️一阶差分➡️二阶差分:

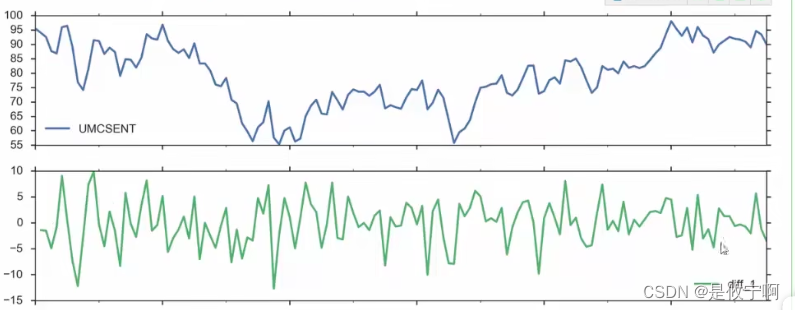
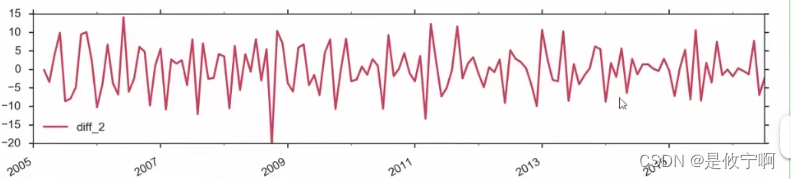
二、arima
1.自回归模型

2.移动平均模型
关注的是误差项的累积


3.arma
p d(几阶差分) q自己指定
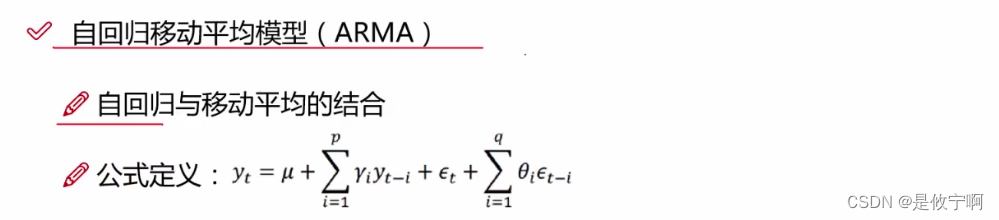
4.总结

三、相关函数
同一个函数在不同阶数的相关系数
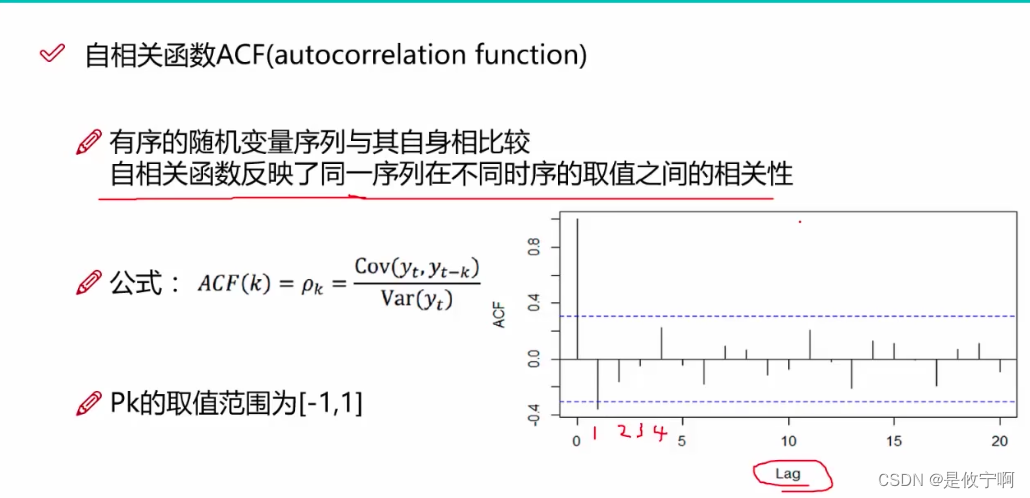
严格两个变量之间的影响,不考虑中间的阶数

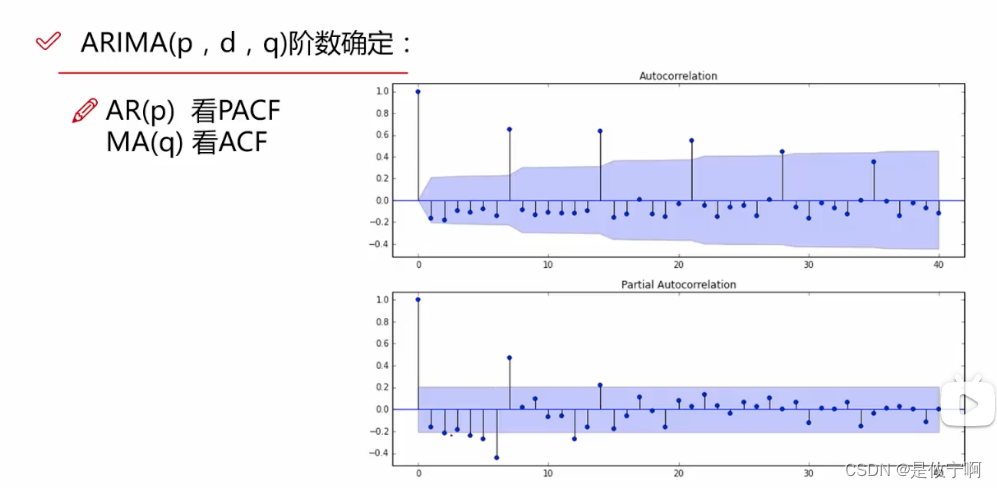
这也可以从自相关系数和偏自相关系数来理解。MA模型的阶数看自相关系数,AR模型的阶数看偏自相关系数。如果自相关系数q阶以后都趋于0,说明是MA(q)模型;这时去看偏自相关系数,必然是无穷阶后都不收敛于0——因为MA模型对应无穷阶的AR模型。同样的,如果偏自相关系数p阶以后都趋于0,说明是AR(p)模型;这时去看自相关系数,必然是无穷阶后都不收敛于0——因为AR模型对应无穷阶的MA模型。
最后,来说说ARMA模型。当自相关系数和偏自相关系数都没有收敛于0,说明这个时间序列不能纯用低阶的AR模型或者纯用低阶的MA模型来解释,需要低阶的AR和低阶的MA模型混合来解释。也可以换个角度来思考,前面提到,任何一个时间序列都可以用纯粹的AR模型来刻画。但是偏自相关系数无穷阶后都不收敛于0,说明只能用一个高阶的AR来解释。但这样的话,阶数太高,待估参数太多,我们就不开心了。所以我们对这个高阶AR模型做分解,分解出一个低阶的AR模型和另一个特殊的高阶AR模型,其中分解出来的高阶AR模型恰好等价于一个低阶的MA模型。于是我们就可以用低阶的AR模型和低阶的MA模型来描述这个时间序列了,这就是ARMA模型
四、模型建立
我个人理解,拖尾就是缓慢落在了置信区间,截尾就是突变,然后后面的数据都在置信区间
结尾意思是落在置信区间 






![[Java基础揉碎]final关键字](https://img-blog.csdnimg.cn/direct/8727d75b8df745cda248eef23ec0ae0a.png)