第十四届蓝桥杯省赛C++ A组所有题目以及题解（C++）【编程题均通过100%测试数据】

第一题《幸运数》【模拟】

【问题描述】

小蓝认为如果一个数含有偶数个数位，并且前面一半的数位之和等于后面一半的数位之和，则这个数是他的幸运数字。例如 2314是一个幸运数字,因为它有4个数位,并且2+3=1+4。现在请你帮他计算从1至100000000之间共有多少个不同的幸运数字。

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

【代码】

#include<iostream>
#include<string>
using namespace std;
typedef long long LL;
LL res;bool check(string s){int l = s.size();int left=0,right=0;for(int i = 0,j=l-1;i<j;i++,j--){left += s[i] - '0';right += s[j] - '0';}if(left==right)return true;return false;
}int main(){//此代码运行会报TLE超时错误，只用于暴力枚举得出答案。for(int i=11;i<1e8;i++){string str = to_string(i);if(str.size()%2!=0)continue;if(check(str)) res++;}cout<<res << endl;return 0;
}

【答案】

4430091

第二题《有奖问答》【模拟】

【问题描述】

小蓝正在参与一个现场问答的节目。活动中一共有30道题目,每题只有答对和答错两种情况,每答对一题得10 分，答错一题分数归零。小蓝可以在任意时刻结束答题并获得目前分数对应的奖项，之后不能再答任何题目。最高奖项需要100 分，所以到达 100 分时小蓝会直接停止答题。请注意小蓝也可能在不到100 分时停止答题。已知小蓝最终实际获得了70分对应的奖项,请问小蓝所有可能的答题情况有多少种?

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

【代码】

#include <iostream>using namespace std;int ans;void dfs(int k, int sum)
{if(sum == 70) //只要70分就记录答案ans++;if(sum == 100 || k >= 30) //100分的时候停止答题return ;dfs(k + 1, sum + 10);dfs(k + 1, 0); //答错归0
}int main()
{//此代码运行会报TLE超时错误，只用于暴搜得出答案。dfs(0, 0);cout << ans << endl;return 0;
}

【答案】

8335366

第三题《平方差》【简单模拟】

【问题描述】

输入两个整数A和B，输出 $A^{2}$ - $B^{2}$ 的值。

【输入格式】

第一行输入一个整数，表示A。

第二行输入一个整数，表示B。

【输出格式】

输出仅一行，包含一个整数，表示答案。

【样例输入】

20

10

【样例输出】

300

【数据范围】

对于所有评测数据， $-10^{100}$ ≤ A,B ≤ $10^{100}$

【思路】

本题使用python将非常方便。

【代码】

print(int(input())**2-int(input())**2)

第四题《更小的数》【区间DP】

【问题描述】

小蓝有一个长度均为 n 且仅由数字字符 0∼9 组成的字符串，下标从 0 到 n−1，你可以将其视作是一个具有 n 位的十进制数字 num，小蓝可以从 num 中选出一段连续的子串并将子串进行反转，最多反转一次。

小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 $num_{new}$ 满足条件 $num_{new}$ <num，请你帮他计算下一共有多少种不同的子串选择方案，只要两个子串在 num 中的位置不完全相同我们就视作是不同的方案。

注意，我们允许前导零的存在，即数字的最高位可以是 0，这是合法的。

【输入格式】

输入一行包含一个长度为 n 的字符串表示 num（仅包含数字字符 0∼9），从左至右下标依次为 0∼n−1。

【输出格式】

输出一行包含一个整数表示答案。

【数据范围】

对于 20% 的评测用例，1≤n≤100；
对于 40% 的评测用例，1≤n≤1000；
对于所有评测用例，1≤n≤5000。

【输入样例】

210102

【输出样例】

8

【样例解释】

【思路】

题解来源： AcWing 4997. 更小的数 - AcWing

先枚举长度，再枚举右端点
1.右端点大于左端点则将dp[l][r]设为1
2.右端点等于左端点，则可以看dp[l−1][r−1]是否为1
3.右端点小于左端点，不进行任何操作

【代码】

#include<iostream>
using namespace std;
const int N=5e3+10;
int n,dp[N][N],res;int main(){string s;cin>>s;n=s.size();for(int len=2;len<=n;++len){for(int l=0;l+len-1<n;++l){int r=l+len-1;if(s[l]>s[r])dp[l][r]=1;else if(s[l]==s[r])dp[l][r]=dp[l+1][r-1];res+=(dp[l][r]==1);}}cout<<res<<endl;return 0;
}

第五题《颜色平衡树》【树上启发式合并】

【问题描述】

给定一棵树，结点由 1 至 n 编号，其中结点 1 是树根。

树的每个点有一个颜色 $C_{i}$ 。

如果一棵树中存在的每种颜色的结点个数都相同，则我们称它是一棵颜色平衡树。

求出这棵树中有多少个子树是颜色平衡树。

【输入格式】

输入的第一行包含一个整数 n，表示树的结点数。

接下来 n 行，每行包含两个整数 $C_{i}$ ， $F_{i}$ ，用一个空格分隔，表示第 i 个结点的颜色和父亲结点编号。

特别地，输入数据保证 $F_{1}$ 为 0，也即 1 号点没有父亲结点。

保证输入数据是一棵树。

【输出格式】

输出一行包含一个整数表示答案。

【数据范围】

对于 30% 的评测用例，n ≤ 200， $C_{i}$ ≤ 200；
对于 60% 的评测用例，n ≤ 5000， $C_{i}$ ≤ 5000；
对于所有评测用例，1 ≤ n ≤ 200000，1 ≤ $C_{i}$ ≤ 200000，0 ≤ $F_{i}$ < i 。

【输入样例】

6
2 0
2 1
1 2
3 3
3 4
1 4

【输出样例】

4

【样例解释】

编号为 1,3,5,6 的 4 个结点对应的子树为颜色平衡树。

【思路】

题解来源：AcWing 4998. 颜色平衡树（dsu on tree） - AcWing

【代码】

#include <cstdio>
#include <algorithm>
#include <cstring>using namespace std;const char lucky[6] = "H8281";
const int N = 2e5 + 20, M = N * 2;int n, m, a[N], ans;
int f[N], g[N];
int idx, to[M], nxt[M], h[N], sz[N], son[N];void add(int u, int v)
{idx ++; to[idx] = v; nxt[idx] = h[u]; h[u] = idx;
}void Dfs1(int u, int pa)
{int v;sz[u] = 1;for(int i = h[u]; i ; i = nxt[i]){v = to[i];if(v == pa) continue;Dfs1(v, u);sz[u] += sz[v];if(sz[v] > sz[son[u]]) son[u] = v;}
}void Clear(int u, int pa)
{int v;g[f[a[u]]] = 0;f[a[u]] = 0;for(int i = h[u]; i ; i = nxt[i]){v = to[i];if(v == pa) continue;Clear(v, u);}
}void collect(int u, int pa)
{int v;f[a[u]] ++;g[f[a[u]] - 1] --;g[f[a[u]]] ++;for(int i = h[u]; i ; i = nxt[i]){v = to[i];if(v == pa) continue;collect(v, u);}
}void Dfs2(int u, int pa)
{int v;for(int i = h[u]; i ; i = nxt[i]){v = to[i];if(v == pa || v == son[u]) continue;Dfs2(v, u);Clear(v, u);}if(son[u]) Dfs2(son[u], u);f[a[u]] ++; g[f[a[u]]] ++; g[f[a[u]] - 1] --;for(int i = h[u]; i ; i = nxt[i]){v = to[i];if(v == pa || v == son[u]) continue;collect(v, u);}if(1ll * g[f[a[u]]] * f[a[u]] == sz[u]) ans ++;
}int main()
{scanf("%d", &n);for(int i = 1; i <= n; i ++){int C, F;scanf("%d%d", &C, &F);a[i] = C; if(F) add(F, i), add(i, F);}Dfs1(1, 0);Dfs2(1, 0);printf("%d\n", ans);return 0;
}

第六题《买瓜》【区间DP】

【问题描述】

小蓝正在一个瓜摊上买瓜。

瓜摊上共有 n 个瓜，每个瓜的重量为 $A_{i}$ 。

小蓝刀功了得，他可以把任何瓜劈成完全等重的两份，不过每个瓜只能劈一刀。

小蓝希望买到的瓜的重量的和恰好为 m。

请问小蓝至少要劈多少个瓜才能买到重量恰好为 m 的瓜。

如果无论怎样小蓝都无法得到总重恰好为 m 的瓜，请输出 −1。

【输入格式】

输入的第一行包含两个整数 n,m，用一个空格分隔，分别表示瓜的个数和小蓝想买到的瓜的总重量。

第二行包含 n 个整数 $A_{i}$ ，相邻整数之间使用一个空格分隔，分别表示每个瓜的重量。

【输出格式】

输出一行包含一个整数表示答案。

【数据范围】

【输入样例】

3 10
1 3 13

【输出样例】

2

【思路】

题解来源：用户登录

1. 深度遍历:首先将所有瓜重量乘以二，避免切一半出现小数的情况，然后按重量将数组重新排序，这样可以减少切的次数，定义一个总重量数组sum【i】，表示从第?个瓜到最后一个瓜的重量之和，可以知道剩余的瓜的总重量，最后就可以深度遍历了：参数分别为目前买的瓜的总重量S，第几个瓜i，切的次数cnt；当目前的瓜的总重量达到要买的重量m，则更新切的最小次数ams。

2. 注：ans最初设定为50因为题目要求中n不超过30 递归出口：当前切的次数比迄今为止最小的次数ans要多则返回没必要再往下遍历。或者指针 i 超出瓜数n，或者目前买的瓜的重量S超出预期mn，再或者如果买当前编号后的瓜都不能满足m则都返回。

3. 接下来就继续遍历分为三种情况：1. 不买当前瓜，则目前要买的总重量S不变，切的次数cnt也不变。 2. 买当前瓜，则目前的总重量变为S+当前瓜的重量a【i】,切的次数不变。3. 买一半的当前瓜，则目前的总重量为S+当前瓜的一半a【i/2】，切的次数cnt加一遍历结束后如果切的次数ans还为之前的设定值，则说明没有更新其值，无法满足返回-1;否则为满足输出ans即可。

【代码】

#include <iostream>
#include <algorithm>
using namespace std;
int n,ans=50;
long long m,a[50],sum[50];
void dfs(long long S,int i,int cnt){if(cnt>=ans) return;if(S==m) ans=cnt;if(i>n||S>m||S+sum[i]<m) return;dfs(S,i+1,cnt);dfs(S+a[i],i+1,cnt);dfs(S+a[i]/2,i+1,cnt+1);
}
int main()
{// 请在此输入您的代码cin>>n>>m;m<<=1;for(int i=0;i<n;++i){cin>>a[i];a[i]<<=1;}sort(a,a+n,greater<>());for(int i=n-1;i>=0;--i){sum[i]=sum[i+1]+a[i];}dfs(0,0,0);if(ans==50){cout<<-1<<endl;}else{cout<<ans<<endl;}return 0;
}

第七题《网络稳定性》【生成树 + 启发式合并】

【问题描述】

有一个局域网，由 n 个设备和 m 条物理连接组成，第 i 条连接的稳定性为 $W_{i}$ 。

对于从设备 A 到设备 B 的一条经过了若干个物理连接的路径，我们记这条路径的稳定性为其经过所有连接中稳定性最低的那个。

我们记设备 A 到设备 B 之间通信的稳定性为 A 至 B 的所有可行路径的稳定性中最高的那一条。

给定局域网中的设备的物理连接情况，求出若干组设备 $x_{i}$ 和 $y_{i}$ 之间的通信稳定性。

如果两台设备之间不存在任何路径，请输出 −1。

【输入格式】

输入的第一行包含三个整数 n,m,q，分别表示设备数、物理连接数和询问数。

接下来 m 行，每行包含三个整数 $u_{i}$ ， $v_{i}$ ， $w_{i}$ ，分别表示 $u_{i}$ 和 $v_{i}$ 之间有一条稳定性为 $w_{i}$ 的物理连接。

接下来 q 行，每行包含两个整数 $x_{i}$ ， $y_{i}$ ，表示查询 $x_{i}$ 和 $y_{i}$ 之间的通信稳定性。

【输出格式】

输出 q 行，每行包含一个整数依次表示每个询问的答案。

【数据范围】

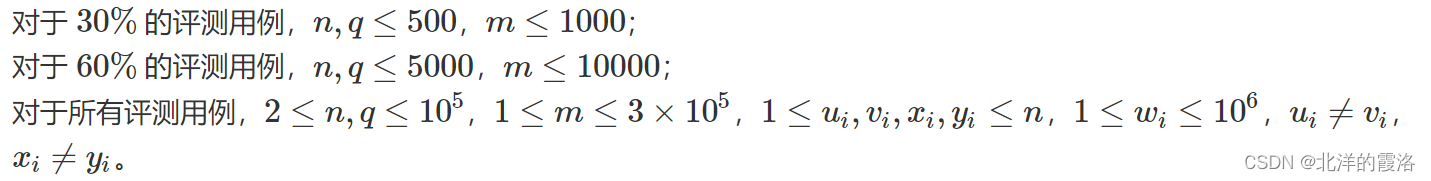
【输入样例】

5 4 3
1 2 5
2 3 6
3 4 1
1 4 3
1 5
2 4
1 3

【输出样例】

-1

3

5

【代码】

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<set>
using namespace std;
const int maxn = 5e5 + 50;
int n, m, q, ans[maxn], fa[maxn];
set<int> query[maxn];
struct road
{int u, v, w;
}st[maxn];
bool cmp(road a, road b) {return a.w > b.w;}
int find(int x) {if (fa[x] != x) {fa[x] = find(fa[x]);}return fa[x];
}
int main()
{cin >> n >> m>>q;memset(ans, -1, sizeof(ans));for (int i = 1;i <= n;i++) {fa[i] = i;}for (int i = 1;i <= m;i++) {cin >> st[i].u >> st[i].v >> st[i].w;}sort(st + 1, st + 1 + m, cmp);for (int i = 1;i <= q;i++) {int a, b;cin >> a >> b;query[a].insert(i);query[b].insert(i);}for (int i = 1;i <= m;i++) {int px = find(st[i].u), py = find(st[i].v), w = st[i].w;if (query[px].size() > query[py].size() ) {swap(px, py);}if (px != py) {vector<int> tmp;for (auto v : query[px]) {if (query[py].count(v)) {ans[v] = w;tmp.push_back(v);}query[py].insert(v);//询问转移}for (auto t : tmp) {query[py].erase(t);//已经完成的询问剃去}fa[px] = py;}}for (int i = 1;i <= q;i++) {cout << ans[i] << endl;}return 0;
}

第八题《异或和之和》【前缀和】

【问题描述】

给定一个数组 $A_{i}$ ，分别求其每个子段的异或和，并求出它们的和。

或者说，对于每组满足 1≤L≤R≤n ，求出数组中第 L 至第 R 个元素的异或和。

然后输出每组 L,R 得到的结果加起来的值。

【输入格式】

输入的第一行包含一个整数 n。

第二行包含 n 个整数 $A_{i}$ ，相邻整数之间使用一个空格分隔。

【输出格式】

输出一行包含一个整数表示答案。

【数据范围】

对于 30% 的评测用例，n ≤ 300；
对于 60% 的评测用例，n ≤ 5000；
对于所有评测用例，1 ≤ n ≤ $10^{5}$ ，0 ≤ $A_{i}$ ≤ $2^{20}$ 。

【输入样例】

5

1 2 3 4 5

【输出样例】

39

【思路】

题解来源：AcWing 5001. 异或和之和 - AcWing

1. 首先借鉴前缀和的想法，将区间操作的时间简化为O(1)，s[i]数组存储的是a[1]到a[i]元素的异或和。由于所求的是所有s[i - 1] ^ s[j]的和，从数的二进制表示出发，给的范围是21位，每一个二进制位最终异或的结果只会是0或者1，就可以遍历这21位每一位，分别求出对总和的贡献。

2. 对于每一个s[i] (这里i枚举的是区间[L, R]的右端点，不需要枚举左端点，只用找前面的0和1)，如果s[i]的第j位是1的，前面的s[a]的第j位是0，s[b]的第j位是1，那么s[i] ^ s[a]的第j位就是1，s[i] ^ s[b]的第j位就是0，s[i] ^ s[b] == 1会对最后的区间和产生贡献，而s[i] ^ s[a] == 0不会，这样只需要统计s[0] ~ s[i]中第j位是0的数组元素的数量就可以得到以i位区间右端点的所有区间对总和(所有区间内异或后的和)。(只需要以O(n)的时间遍历一次数组就可以得出，而不需要遍历两重端点)

3. 具体来说，按照给的参考例子，数组1 2 3 4 5，对应的s数组为0 1 3 0 4 1(s[0] ~ s[5])
s[0] = 0 = 0 0 0 0, s[1] = 1 = 0 0 0 1, s[2] = 3 = 0 0 1 1, s[3] = 0 = 0 0 0 0, s[4] = 4 = 0 1 0 0, s[5] = 1 = 0 0 0 1显然只用考虑二进制的前3位，第1位为0 1 1 0 0 1，从第一个元素开始，1之前只有s[0]为0，所以贡献为1，第二个1前有0 和 1，0的数量为1，贡献为1 + 1 = 2，第三个0前面有两个1，贡献为2 + 2 x 1 = 4，第四个0同样，贡献为4 + 2 x 1 = 6，最后的1前面有3个0，所以二进制第一位的总贡献为6 + 3 * 1 = 9。同理，二进制第二位，第三位的贡献为10 和 20，这样算出来区间和为39。

【代码】

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>using namespace std;typedef long long LL;const int N = 1e5 + 10;int n;
int a[N], s[N];//a[N]中每个数字都是20位的二进制数，所以区间异或和取决于同一位1的奇偶数//100分int main()
{cin >> n;for (int i = 1; i <= n; i ++ ) cin >> a[i];for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] ^ a[i];LL ans = 0;for (int j = 0; j < 21; j ++ ) //枚举每一位，给的Ai范围是0 ~ 2^20{int c0 = 1, c1 = 0; //s[0]始终为0，所以多一个c0 = 1LL now = 0; //当前位的答案for (int i = 1; i <= n; i ++ )if (s[i] >> j & 1) now += c0, c1 ++ ; //s[i]的第j位是1else now += c1, c0 ++ ; //s[i]的第j位是0ans += now * (1 << j);}cout << ans << endl;return 0;
}

第九题《像素放置》【DFS+BFS+剪枝】

【问题描述】

小蓝最近迷上了一款名为《像素放置》的游戏，游戏在一个 n×m的网格棋盘上进行，棋盘含有 n 行，每行包含 m 个方格。

玩家的任务就是需要对这 n×m 个方格进行像素填充，填充颜色只有黑色或白色两种。

有些方格中会出现一个整数数字 x(0≤x≤9)，这表示当前方格加上周围八个方向上相邻的方格（分别是上方、下方、左方、右方、左上方、右上方、左下方、右下方）共九个方格内有且仅有 x 个方格需要用黑色填充。

玩家需要在满足所有数字约束下对网格进行像素填充，请你帮助小蓝来完成。

题目保证所有数据都有解并且解是唯一的。

【输入格式】

输入的第一行包含两个整数 n,m，用一个空格分隔，表示棋盘大小。

接下来 n 行，每行包含 m 个字符，表示棋盘布局。字符可能是数字 0∼9，这表示网格上的数字；字符还有可能是下划线（ASCII 码为 95），表示一个不带有数字的普通网格。

【输出格式】

输出 n 行，每行包含 m 个字符，表示答案。

如果网格填充白色则用字符 0 表示，如果网格填充黑色则用字符 1 表示。

【数据范围】

对于 50% 的评测用例，1 ≤ n,m ≤ 5；
对于所有评测用例，1 ≤ n,m ≤ 10。

【输入样例】

6 8
_1__5_1_
1_4__42_
3__6__5_
___56___
_688___4
_____6__

【输出样例】

00011000
00111100
01000010
11111111
01011110
01111110

【样例解释】

【思路】

题解来源：AcWing 5002. 像素放置 - AcWing

【代码】

#include <bits/stdc++.h>using namespace std;
const int N = 1e3 + 10;
int a[N][N];
bool mp[N][N];
bool used[N][N];
int check[N][N];
int dx[] = {1, 1, 1, 0, 0, -1, -1, -1, 0}, dy[] = {-1, 0, 1, 1, -1, -1, 0, 1, 0};
int n, m;
int cnt;
int answer[N][N];
struct EDGE{int x, y;
}edge[N];
int res;
void bfs(int a, int b){queue<EDGE> q;q.push({a, b});used[a][b] = 1;while(q.size()){EDGE t = q.front();q.pop();edge[++ cnt] = {t.x, t.y};for(int i = 0; i < 8; i ++){int xx = dx[i] + t.x, yy = dy[i] + t.y;if(xx < 1 || xx > n || yy < 1 || yy > m) continue;if(used[xx][yy]) continue;used[xx][yy] = 1;q.push({xx, yy});}}
}
void dfs(int u, int ans)
{if(ans == res){for(int i = 1; i <= n; i ++){for(int j = 1; j <= m; j ++){cout << answer[i][j];}cout << endl;}exit(0);}if(u == cnt + 1) return ;int x = edge[u].x, y = edge[u].y;bool flag = 1, flag1 = 1;for(int i = 0; i < 9; i ++){int xx = x + dx[i], yy = y + dy[i];if(xx < 1 || xx > n || yy < 1 || yy > m) continue;if(!mp[xx][yy]) continue;if(a[xx][yy] == 0){flag = 0;}if(9 - check[xx][yy] ==  a[xx][yy]) flag1 = 0;if(!flag && !flag1) break;}if(flag){answer[x][y] = 1;for(int i = 0; i < 9; i ++){int xx = x + dx[i], yy = y + dy[i];if(xx < 1 || xx > n || yy < 1 || yy > m) continue;if(!mp[xx][yy]) continue;a[xx][yy] --;if(a[xx][yy] == 0) ans ++;check[xx][yy] ++;}dfs(u + 1, ans);    for(int i = 0; i < 9; i ++){int xx = x + dx[i], yy = y + dy[i];if(xx < 1 || xx > n || yy < 1 || yy > m) continue;if(!mp[xx][yy]) continue;if(a[xx][yy] == 0) ans --;a[xx][yy] ++;check[xx][yy] --;}answer[x][y] = 0;}if(flag1){for(int i = 0; i < 9; i ++){int xx = x + dx[i], yy = y + dy[i];if(xx < 1 || xx > n || yy < 1 || yy > m) continue;if(!mp[xx][yy]) continue;check[xx][yy] ++;}dfs(u + 1, ans);    for(int i = 0; i < 9; i ++){int xx = x + dx[i], yy = y + dy[i];if(xx < 1 || xx > n || yy < 1 || yy > m) continue;if(!mp[xx][yy]) continue;check[xx][yy] --;}   }
}
int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++){for(int j = 1; j <= m; j ++){char c;cin >> c;if(c == '_') {mp[i][j] = 0;}else{mp[i][j] = 1;a[i][j] = c - '0';if(c != '0') res ++;}}}for(int i = 1; i <= n; i ++){for(int j = 1; j <= m;j ++){if(!used[i][j])bfs(i, j);}}memset(used, 0, sizeof used);dfs(1, 0);return 0;
}

第十题《翻转硬币》【杜教筛+整除分块】

【问题描述】

给定 n 个按顺序摆好的硬币，一开始只有第 1 个硬币朝下，其他硬币均朝上。

你每次操作可以选择任何一个整数 i 并将所有满足 j mod i=0 的位置 j 的硬币翻转。

求最少需要多少次操作可以让所有硬币都朝上。

【输入格式】

输入一行包含一个整数 n。

【输出格式】

输出一行包含一个整数表示最少需要的操作次数。

【数据范围】

对于 30% 的评测用例，n ≤ 5× $10^{6}$ ；
对于 70% 的评测用例，n ≤ $10^{9}$ ；
对于所有评测用例，1 ≤ n ≤ $10^{18}$

【输入样例1】

7

【输出样例1】

6

【输入样例2】

1131796

【输出样例2】

688042

【思路】

题解来源：AcWing 5003. 翻转硬币 - AcWing

【代码】

#include <iostream>
#include <unordered_map>
#include <cmath>using namespace std;const int N = 20000010;using i64 = long long;int primes[N], cnt;
bool st[N];
int mu[N];
unordered_map<int, int> ans_mu;void init(int n) {mu[1] = 1;for (int i = 2; i <= n; i++) {if (!st[i]) {primes[cnt++] = i;mu[i] = -1;}for (int j = 0; j < cnt && primes[j] * i <= n; j++) {int x = primes[j];st[i * x] = true;if (i % x == 0) {break;} else {mu[i * x] = -mu[i];}}}for (int i = 1; i <= n; i++) mu[i] += mu[i - 1];
}int sum_mu(int n) {if (n <= 20000000) return mu[n];if (ans_mu.count(n)) return ans_mu[n];i64 res = 1;for (i64 l = 2, r; l <= n; l = r + 1) {r = n / (n / l);res -= (r - l + 1) * sum_mu(n / l);}return ans_mu[n] = res;
}int main() {init(20000000);i64 n;cin >> n;i64 res = 0;for (i64 l = 1, r; l <= n / l; l = r + 1) { r = sqrt(n / (n / l / l));res += (sum_mu(r) - sum_mu(l - 1)) * (n / (l * l));}cout << res << '\n';return 0;
}

以上内容部分题目题解摘自他人博客题解，在题目处均已标明出处。若有侵权，私信删除。