一、说明
在我之前的博客中,我们研究了关于生成式预训练转换器的整个概述,以及一篇关于生成式预训练转换器(GPT)的博客——预训练、微调和不同的用例应用。现在让我们看看所有仅解码器模型的解码策略是什么。
二、解码策略
在之前的博客中,我们将转换器视为一个函数,它接受输入并开始生成下一个标记或输出,同时进行自回归,即它在所有步骤中将自己的输出作为输入并生成输出。
在训练过程中,我们也以类似的方式进行训练,因为我们展示了某些文本,我们知道下一个单词是什么,我们要求它预测下一个标记是什么,然后根据最大标记的概率反向传播损失。下一个代币预测的想法可以迭代完成,以生成我们想要的任意数量的代币,并且可能会生成完整的故事。
例如,假设一个句子“你能不能拿一个从前开始的故事”,所以整个事情已经成为给模型的第一个“k”个标记,从这个时间步长开始,我们需要生成一个故事,其中标记的预测发生,直到我们满意或一旦我们到达序列的末尾<eos>。
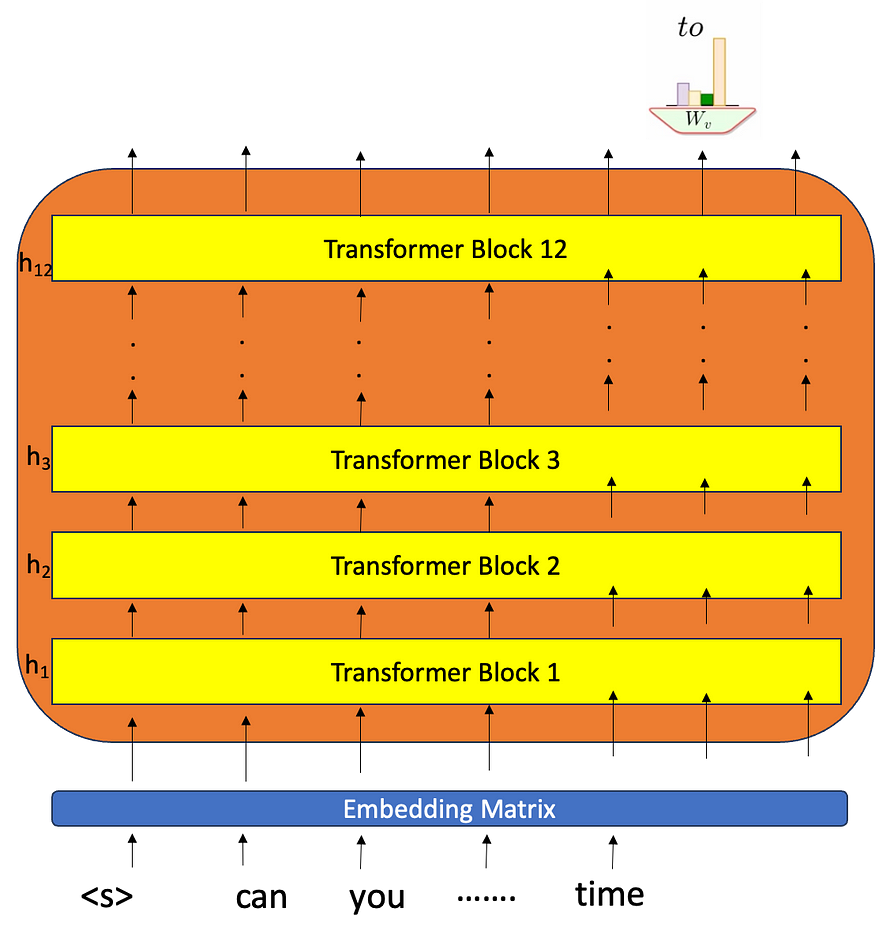
鉴于模型已经过训练来预测下一个标记和一些额外的东西,我们将做一些称为“指令微调”的事情,现在我们希望模型在我给它某些输入的场景中工作,它必须从那里开始继续答案,所以给出的任何问题,或者如果给出一些段落并要求总结,那么它必须总结。
最初的微调问题,如预测情绪或像两个句子一样,是相似还是不相似——与我们使用现代 LLM 应用程序看到的相比,这些要容易得多,这些应用程序是更具创造性的应用程序,如(写诗等、写简历、建立网站等),所以这些是目前让我们感到惊讶的事情。显然,目前我们不知道这些高级 LLM(大型语言模型)如何能够产生如此精确和创造性的输出,但我们目前看到的是关于下一个单词预测如何发生的解码部分——我们知道的一件事是,如果我们要选择最大概率标记的过程,那么显然我们将获得与此相同的标记输出确定性输出。现在让我们看一些或一些解码策略,其中我们为每个策略都有一些创造性的输出,其中确定性将提供相同的输出,随机性将产生不同的输出。

详尽搜索:
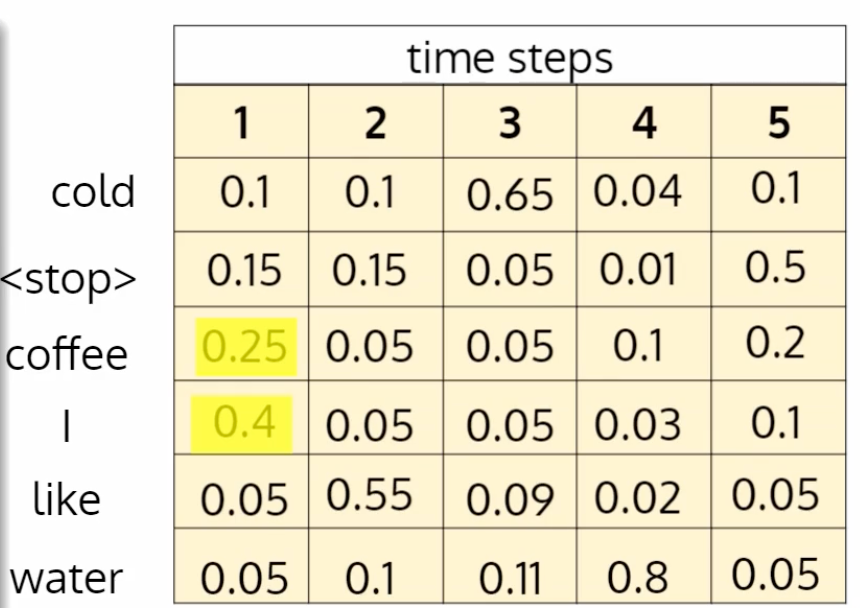
假设我们想生成一个 5 个单词的序列,词汇表为 { cold, coffee, I , like , water, <stop>}
穷举搜索所有可能的序列和相关的概率,并输出具有最高概率的序列。
- 我喜欢冷水
- 我喜欢冷咖啡
- 像冷咖啡一样的咖啡
- 我喜欢我喜欢
- 咖啡 咖啡 咖啡 咖啡
因此,对于每个句子输出,概率将是
P(x1, x2, x3,.....xn) = P(x1).P(x2/x1), ..........., P(xn/x1, x2, ......xn-1)
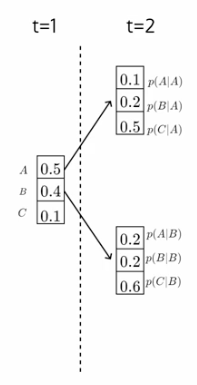
由于这是详尽的搜索 - 我们将通过解码过程找到所有可能的序列。在每个时间步长中,我们将传递所有单词

由于这里有 6 个单词,我们可以有这 6 个单词的分布,如下所示。
如果其中一个示例输入序列是“我喜欢冷咖啡<停止>”
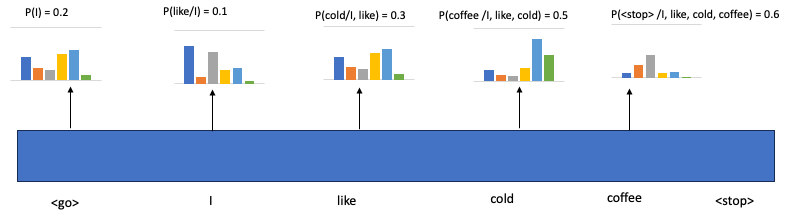
上述序列的总概率将等于
P(I) * P(like/I)*P(冷/I,like)*P(咖啡/I,like,冷)
同样,序列的其他组合也将遵循与上述相同的模式,并给我们提供具有最大概率的输出——这种概率计算是在每个时间步对所有标记完成的。
因此,基于上述详尽的搜索,让我们假设这些是搜索空间中的概率
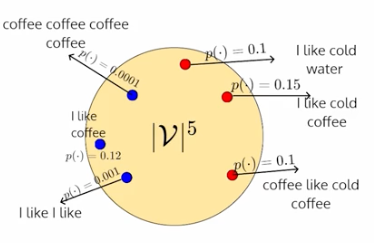
假设该序列在所有 |v|⁵ 序列中具有最高的概率——在上面的本例中,如果生成“我喜欢冷咖啡”序列作为最高概率,则结果将突出显示

通过这种详尽的搜索,无论我们计算多少次——对于给定的相同输入,我们都会得到相同的答案,我们看不到任何创造性的输出。这属于确定性策略。包含所有树类型输出的最终示例图如下所示 —
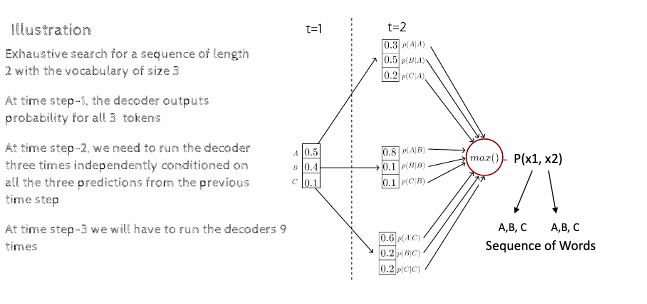
在这 9 种可能性中,以最大概率为准,它在时间步长 =2 时给出输出。如果我们的时间步长 = 3,那么我们将有 27 个具有概率的序列,并且我们对所有这 27 个序列都获得最高分。
如果 |v|= 40000,那么我们需要并行运行解码器 40000 次。
贪婪的搜索:
使用贪婪搜索 - 在每个时间步,我们总是以最高的概率输出令牌(贪婪)
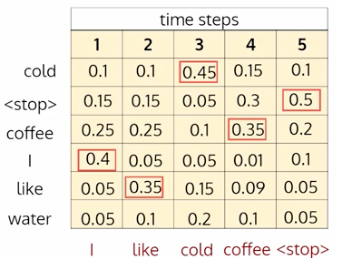
p(w2 = like|w1=I) = 0.35
p(w3= 冷 | w1,w2) = 0.45
p(w4 = 咖啡 |w1,w2,w3) = 0.35
p(w5 = 止损 | w1, w2, s3, s4) = 0.5
则生成序列的概率为
p(w5,w1,w2,w3,w4) = 0.5*0.35*0.45*0.35*0.5 = 0.011

三、一些局限!
Is this the most likely sequence?
如果我们想得到各种相同长度的序列怎么办?
如果起始标记是单词“I”,那么它最终总是会产生相同的序列:我喜欢冷咖啡。
如果我们在第一个时间步中选择了第二个最可能的代币怎么办?
然后,后续时间步长中的条件分布将发生变化。则生成序列的概率为
p(w5,w1,w2,w3,w4) = 0.25*0.55*0.65*0.8*0.5 = 0.035
如果我们在第一个时间步中选择了第二个最可能的代币怎么办?
然后,后续时间步长中的条件分布将发生变化。那么生成的序列的概率为
p(w5,w1,w2,w3,w4) = 0.25*0.55*0.65*0.8*0.5 = 0.035

我们可以输出这个序列,而不是贪婪搜索生成的序列。当我们发送相同的输入令牌时,这也将产生相同的输出。贪婪地选择具有最大概率的令牌,每个时间步长并不总是给出具有最大概率的序列。
光束搜索:
不要考虑每个时间步长的所有标记的概率(如在穷举搜索中),而只考虑 top-k 标记
假设 (k=2),在时间步长 = 2 时,我们有两个概率为 I , cold 的标记,我们将有 12 个这样的序列。

现在我们必须选择使序列概率最大化的标记。它需要 k x |v|每个时间步的计算。在第二个时间步长,我们有 2 x 6=12 次计算,然后进行排名,我们选择最高概率序列。
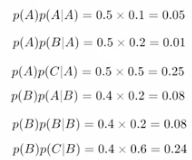
让我们从上述概率分数中选出前 2 名。

按照类似的计算,我们最终选择时间步长 = 3 和 3 个单词或标记
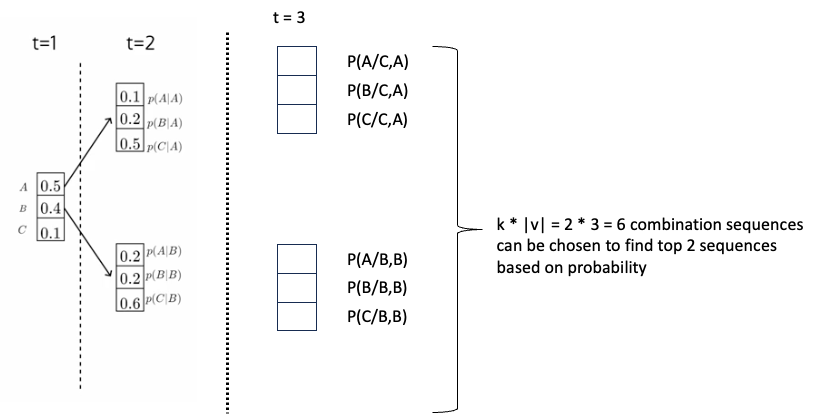
现在,我们将在时间步长 T 的末尾有 k 个序列,并输出概率最高的序列。
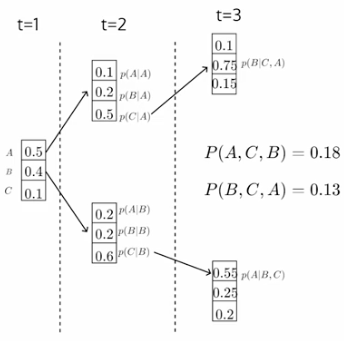
参数 k 称为光束尺寸。它是穷举搜索的近似值。如果 k = 1,则它等于贪婪搜索。如果 k > 1,则我们正在进行波束搜索,如果 k = V,则我们正在进行穷举搜索。
现在让我们举一个例子,k = 2,标记词汇是 |v|。

以上 2 * |V|我们将再次取前 2 个概率的值

我们将有更多这样的序列,我们将只有 2 个序列继续前进——所以最后我们的流程图看起来像这样

- 贪婪搜索和光束搜索都容易退化,即它们可能是重复的,没有任何创造力。
- 贪婪搜索的延迟低于波束搜索
- 贪婪的搜索和光束搜索都无法产生创造性的输出
- 但请注意,波束搜索策略非常适合翻译和摘要等任务。
基本上,我们需要一些带有创造性答案或输出的惊喜——因此我们需要一些基于采样的策略,而不需要贪婪或光束搜索。
四、抽样策略 — Top -K
在这里,在每个时间步长中,考虑概率分布中的 top — k 个标记。
从 top-k 令牌中对令牌进行采样。假设 k = 2
在对代币进行采样之前,top-k 代币的概率将相对归一化为 , P(I) = 0.61 ~ (0.25/ (0.25+0.4)), P(Coffee) = 0.39 ~ 0.4/(0.25+0.4)。

让我们假设并创建一个随机数生成器,它预测介于 0 和 1 之间 — rand(0,1)。假设如果获得的数字是 ~0.7,那么咖啡将是作为输入的单词或标记,如果再次生成的随机数是 ~0.2,那么在时间步长 2 中,单词或标记“I”将是输入。


对前 2 个单词使用 top-K 采样生成的序列是
就像<停下来一样>
等价和<止损>的归一化概率分别为 0.15/(0.55+0.15)~0.23 和 0.55/(0.55+0.15) ~0.77。

现在我们运行 Rand 函数来生成从 0 到 1 的数字——假设如果值为 0.9,则输出<stop> 将是输出,那么结果过程将就此停止。下次当随机生成器输出为 0.5 时,我们将以“喜欢”作为结果。因此,通过进行这种随机生成,我们将获得不同的输出。可能是第一个“我”,生成“<停止>”——对于所有其他情况,结果可能会有所不同,如下所示。

惊喜是随机的结果。波束搜索与人类预测在每个时间步长上的预测相比如何?
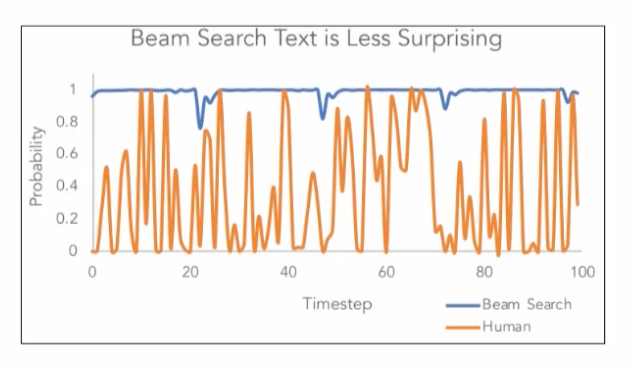
如果我们看一下波束搜索,它会以非常高的概率产生输出,因此我们看不到任何惊喜——但是如果要求人类填写句子,我们将得到不同和随机的结果,概率非常小,因为人类预测具有高方差,而波束搜索预测具有低方差。给其他极有可能的代币一个机会会导致生成的序列出现多样性。
假设我们有 40K 词汇表中的前 5 个单词(I、go、where、now、then),概率分别为 (0.3、0.2、0.1、0.1、0.3)。

如果随机生成器生成任意数字 b/w 0 和 1,并且基于该值,我们将选择或采样单词或标记以选择高概率值。我们必须记住,在这里我们不是从 40K 词汇表中随机选择样本,而是我们正在做的是,我们已经从 40K 词汇表中获得了前 5 个单词,并且从前 5 个单词或样本的子集中,我们正在创建序列——这里它是随机的,但它是序列的受控随机选择。
五、抽样策略 — Top -P
k 的最优值应该是多少?
让我们举 2 个例子,分别是平坦分布和峰值分布。
示例-1:(平坦分布)

示例 — 2:(峰值分布)
根据分布类型,K 的值会有所不同——如果我们有一个峰值分布,那么与平坦分布相比,K值高一点将无济于事。
如果我们修复 的 vlaue,比如 k = 5,那么我们就会从平坦分布中遗漏其他同样可能的标记。
它会错过生成各种句子(创意较少)
对于峰值分布,使用相同的值 k = 5,我们最终可能会为更少的句子创造一些意义。
解决方案 — 1 : 低温采样

当温度 = 1 时,这就是正态 softmax 方程的分布。给定 logits,u1: |v|和温度参数 T ,计算概率为

如果我们减小 T 值,我们会得到峰值分布。
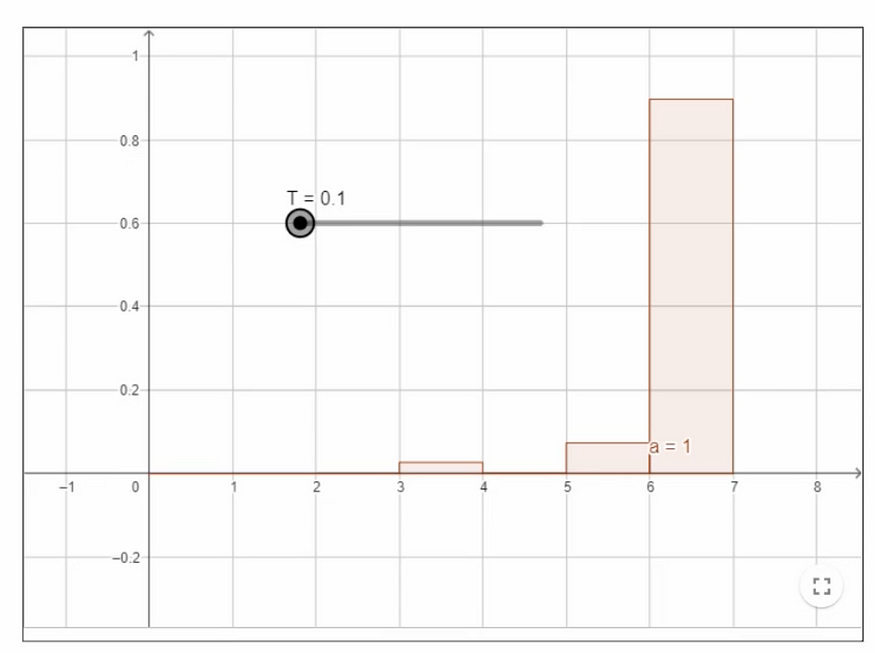
- 低温 = 偏态分布 = 创造力降低
- 高温 = 更平坦的分布 = 更多的创造力
解决方案 — 2: 顶部 — P(原子核)采样
让我们再考虑上面的两个例子。
- 按降序对概率进行排序
- 设置参数 p, 0 < p < 1 的值
- 将代币从顶部代币开始的概率相加
- 如果总和超过 p,则从所选令牌中抽取令牌
- 它类似于 top-k,k 是动态的。假设我们将 p = 0.6 设置为阈值,
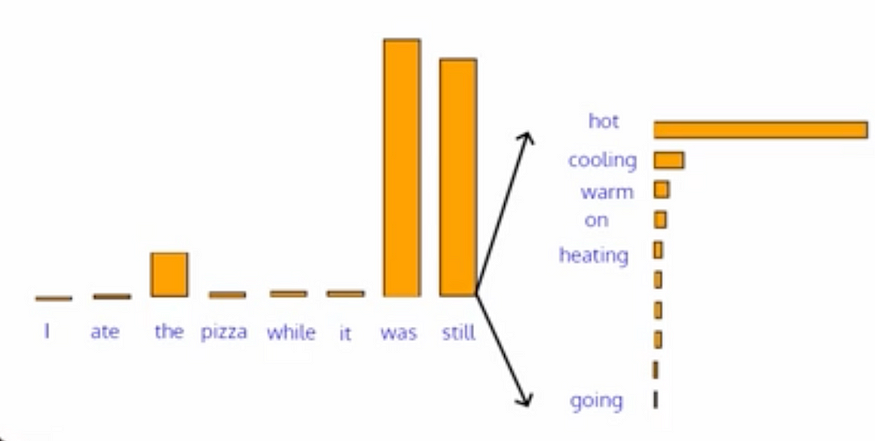
例如,-1 分布:该模型将从标记中采样(思想、知道、有、看到、说)

例如-2 分布:模型将从令牌中采样(热、冷却)
根据生成的随机值,我们将选择不同的单词标记进行序列形成。
这是对仅解码器模型的所有解码策略的总结,即我们在确定性和随机性上徘徊的 GPT——这种随机策略确保即使 transformer 具有确定性的计算输出,但最后我们将添加一个采样函数,这将确保我们每次都采样不同的令牌,从而生成不同的序列。