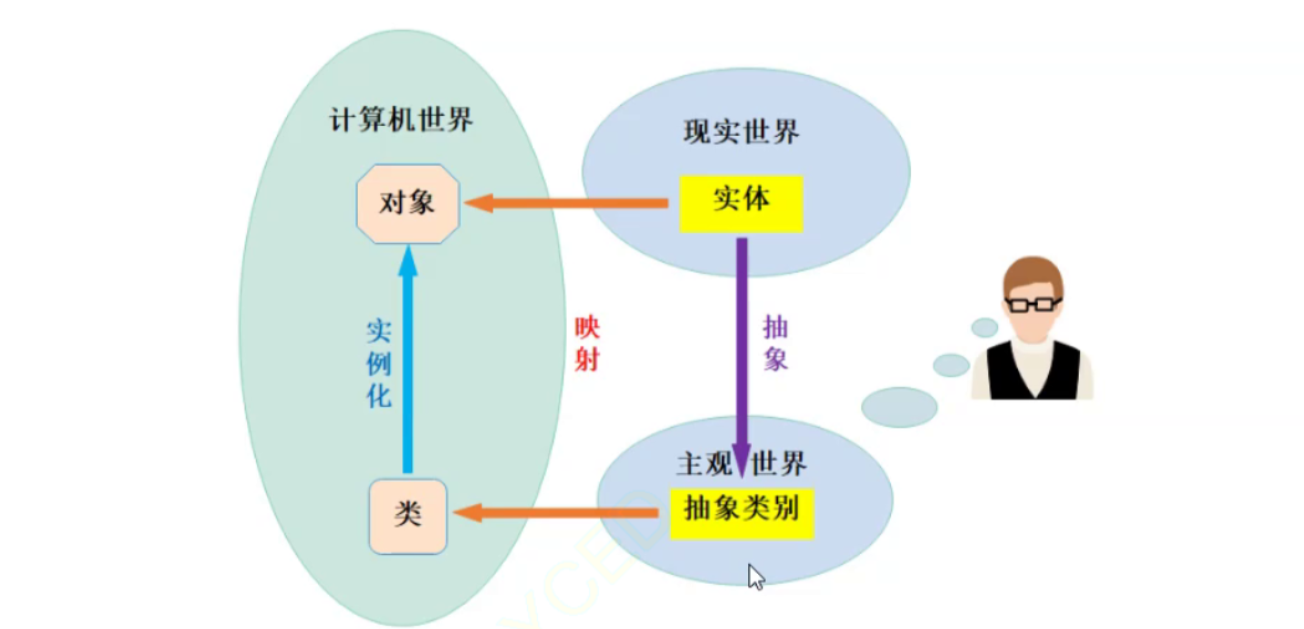
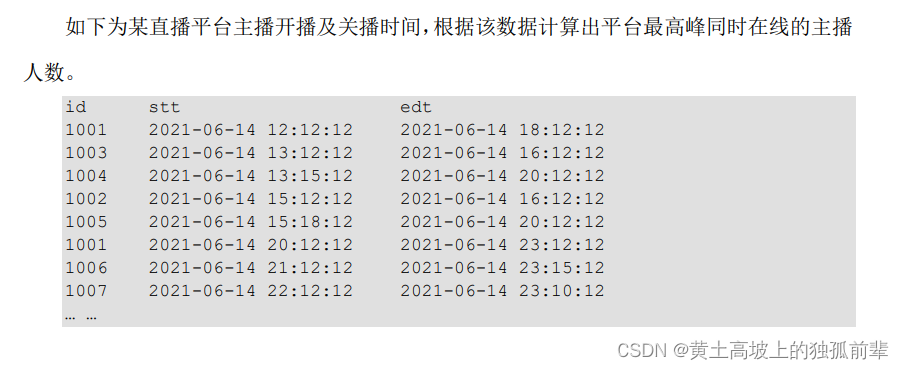
一、引言
在互联网产品优化和运营策略制定中,AB测试(也称为分组测试或随机化对照实验)是一种科学且严谨的方法。它通过将用户群体随机分配至不同的实验组(通常是A组和B组),对比不同版本的产品或策略对关键指标的影响,以此做出最优决策。本文将详细介绍AB测试的基本原理、实施步骤,并通过实际案例进行深度剖析。

二、AB测试基本原理
AB测试的核心在于“控制变量法”,即保持其他条件不变,仅改变一个因素(如产品设计、营销策略等),观察其对目标变量(如转化率、留存率等)的影响。例如,对于一款APP,我们可以为一部分用户展示新版的登录界面(B组),而另一部分用户则继续使用旧版界面(A组)。通过比较两组用户的登录转化率,可以判断新版界面是否优于旧版。
三、AB测试实施步骤
1. 定义问题和假设:首先明确要解决的问题或者要验证的假设,比如,“修改登录界面设计能否提高用户的登录转化率?”
2. 设定实验组与对照组:将用户随机分配至实验组(B组,接受新设计)和对照组(A组,维持原状)。
3. 选择关键指标:确定用于评估效果的关键性能指标(KPI),如点击率、转化率、留存率等。
4. 执行测试并收集数据:在一定时间内运行AB测试,确保样本量足够大以获得统计显著性。
5. 数据分析与解读结果:运用统计学方法对收集的数据进行分析,判断新方案是否优于原方案。
6. 决策与迭代:基于实证结果作出决策,如果新方案有效,则推广;无效则回滚或进一步优化。
四、AB测试实战案例
以某电商平台为例,该平台决定对商品详情页的设计进行优化,提出两个设计方案——A方案和B方案。通过AB测试,将用户流量均匀分为两部分,分别采用两种设计方案。
经过一段时间的测试后,发现B方案的商品详情页布局使得用户停留时间增长了15%,并且购物车添加率提高了10%。经统计检验,这些差异具有统计显著性。因此,平台方有足够的证据支持采用B方案的新设计。
五、AB测试中的统计学知识
AB测试的成功实施离不开统计学的支持。以下是几个关键的统计学概念和方法:
1. 样本大小与功效分析
在启动AB测试前,需要预先确定足够的样本大小,这可以通过功效分析来完成。功效分析主要考虑的因素包括预设的最小效应值(即新方案相比于原方案至少需要多大的改进才能被认为是有效的)、显著性水平α(一般取0.05,表示犯第一类错误的概率)、以及功效(即当真实存在效应时,检测出这个效应的概率,通常希望大于80%或90%)。
2. 假设检验
在AB测试中,我们通常采用双尾或单尾假设检验来确定实验结果是否显著。例如,零假设(H0)可能是“新旧方案的转化率无差异”,备择假设(H1)则是“新方案的转化率高于(或低于)旧方案”。通过计算p值,若p值小于预设的显著性水平α,则拒绝零假设,认为新方案在统计上显著优于旧方案。
3. 分布与置信区间
在衡量效果时,我们不仅关注点估计(如平均转化率),还要计算置信区间,了解估计的稳定性和精确度。例如,95%的置信区间意味着如果重复多次实验,95%的情况下真实的平均转化率会落入该区间内。
4. 多重比较与矫正
在进行多个AB测试时,如果没有进行适当的统计矫正,可能会增加犯第一类错误(假阳性)的概率。Bonferroni校正、Sidak校正、Holm-Bonferroni校正等方法可以帮助我们在面对多重比较问题时,保持整体的错误率在可接受范围内。
五、AB测试实例及代码分析
为了更直观地理解AB测试及其背后的统计学原理,我们将通过Python编程语言和一种常用的统计库——`statsmodels`来进行一个实际的AB测试分析示例。
假设一家电商网站对商品详情页面进行了优化(B版本),希望通过AB测试判断优化后的页面是否提升了用户的购买转化率。已有的原始数据如下:
import pandas as pd
import numpy as np
from statsmodels.stats.proportion import proportions_ztest
# 伪造AB测试数据
np.random.seed(123)
control_group = np.random.binomial(1, 0.1, size=1000) # 对照组(A组)1000个用户,转化率为10%
treatment_group = np.random.binomial(1, 0.15, size=1000) # 实验组(B组)1000个用户,转化率为15%
data = {
'group': ['A'] * 1000 + ['B'] * 1000,
'converted': control_group.tolist() + treatment_group.tolist()
}
df = pd.DataFrame(data)
print(df.head())
接下来,我们将利用`statsmodels`库进行假设检验,看B组的转化率是否显著高于A组:
# 计算各组转化人数和总人数
n_A = df[df['group'] == 'A']['converted'].sum()
N_A = df[df['group'] == 'A']['converted'].count()
n_B = df[df['group'] == 'B']['converted'].sum()
N_B = df[df['group'] == 'B']['converted'].count()
# 使用proportions_ztest进行假设检验
z_statistic, p_value = proportions_ztest([n_A, n_B], [N_A, N_B], alternative='larger')
# 输出结果
print("Z-统计量: ", z_statistic)
print("P值: ", p_value)
假设我们的显著性水平α设置为0.05,如果得到的P值小于0.05,那么我们就可以拒绝零假设,认为B组的转化率显著高于A组。
在上述代码中,`proportions_ztest`函数是基于二项分布的正态近似进行的假设检验,这里使用的“larger”参数代表我们是在做单尾检验,即只关心B组转化率是否更高。
七、总结
AB测试是一个涉及统计推断和决策的过程,要求我们在设计实验时,充分考虑统计学原理,合理确定样本大小,正确使用假设检验和置信区间,以及处理好多重比较问题。只有这样,我们才能从海量数据中提取出可靠的信息,科学地指导产品优化和业务决策。
AB测试是数据驱动决策的重要工具,能帮助我们避免主观臆断,用事实说话,精准提升产品性能和用户体验。但在实际应用中,还需要注意避免常见误区,如样本偏差、多重测试陷阱等问题,确保测试结果的有效性和可靠性。
以上只是AB测试的基础知识和实战应用初步介绍,深入实践还需结合具体业务场景灵活运用,持续优化,从而实现产品的精细化运营和持续增长。