今日任务:
1)513.找树左下角的值
2)112.路径总和
3)113.路径总和Ⅱ
4)106.从中序与后序遍历序列构造二叉树
5)105.从前序与中序遍历序列构造二叉
513.找树左下角的值
题目链接:513. 找树左下角的值 - 力扣(LeetCode)
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。假设二叉树中至少有一个节点。
示例 1:
输入: root = [2,1,3]
输出: 1示例 2:
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7
文章讲解:代码随想录 (programmercarl.com)
视频讲解:怎么找二叉树的左下角? 递归中又带回溯了,怎么办?| LeetCode:513.找二叉树左下角的值哔哩哔哩bilibili
层次遍历——思路:
首先最简单直接的就是采用层次遍历,收集每一层元素,最后返回最后一层的第一个元素result[-1][0]
稍微改进一下就是,遍历每一层时,只取队列的首位
# Definition for a binary tree node.
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = right# 层次遍历
class Solution:def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:if not root:return 0queue = collections.deque([root])result = []while queue:queue_size = len(queue)level = []for _ in range(queue_size):node = queue.popleft()level.append(node.val)if node.left:queue.append(node.left)if node.right:queue.append(node.right)result.append(level)return result[-1][0]# 改进def findBottomLeftValue2(self, root: Optional[TreeNode]) -> int:if not root:return 0queue = collections.deque([root])result = 0while queue:queue_size = len(queue)for i in range(queue_size):node = queue.popleft()if i == 0:result = node.valif node.left:queue.append(node.left)if node.right:queue.append(node.right)return result递归(DFS)——思路
核心是找到最后一行的最左侧节点,这个节点不一定是左节点。如果采用递归的话
1.我们要明确递归函数的参数和返回值
这里我们需要记录深度,所以传参除了常规的节点外,还需要传入深度,遍历过程中还需注意深度的回溯。整个过程中,我们需要有一个变量记录最大深度,一个变量记录最大深度第一次出现时叶子节点的值,这两个参数可以作为传参,也可以设为全局变量。
返回值则为最大深度第一次出现时的叶子节点
2.确定终止条件
当遇到叶子节点时,需要更新最大深度,如果此时深度比之前记录的最大深度大,那么同时也要更新记录返回值的变量
3.确定单层递归的逻辑
保证先左后右即可,这样第一次出现最大深度的节点一定在最左侧
class Solution:def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:self.result = Noneself.maxDepth = float('-inf')self.getLeftNode(root, 0)return self.resultdef getLeftNode(self, node, depth):# 判断该节点是否为叶子节点,是则终止if node.left is None and node.right is None:if depth > self.maxDepth:self.result = node.valself.maxDepth = depthreturnif node.left:depth += 1self.getLeftNode(node.left, depth)depth -= 1if node.right:depth += 1self.getLeftNode(node.right, depth)depth -= 1精简版:隐藏回溯
# 递归精简(隐藏回溯)
class Solution3:def findBottomLeftValue(self, root: TreeNode) -> int:self.max_depth = float('-inf')self.result = Noneself.traversal(root, 0)return self.resultdef traversal(self, node, depth):if not node.left and not node.right:if depth > self.max_depth:self.max_depth = depthself.result = node.valreturnif node.left:self.traversal(node.left, depth + 1)if node.right:self.traversal(node.right, depth + 1)
112. 路径总和
题目链接:
112. 路径总和 - 力扣(LeetCode)
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例: 给定如下二叉树[5,4,8,11,None,13,4,7,2,None,None,1],以及目标和 sum = 22,
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
文章讲解:代码随想录 (programmercarl.com)
视频讲解:拿不准的遍历顺序,搞不清的回溯过程,我太难了! | LeetCode:112. 路径总和哔哩哔哩bilibili
112.路径总和——思路:
DFS深度优先遍历算法,前序遍历,每次遍历采用目标值去减当前节点,
一旦出现差值div为0,可以判断是否是叶子节点,是叶子节点返回true
如果遍历到叶子节点,div != 0 继续遍历
这题也要注意回溯过程
class Solution:def hasPathSum(self, root: TreeNode, targetSum: int) -> bool:if not root:return Falsediv = targetSum - root.valreturn self.traversal(root, div)def traversal(self, node, div):# 终止条件if not node.left and not node.right:if div == 0:return Trueelse:return Falseif node.left:div -= node.left.valif self.traversal(node.left, div): # 左return Truediv += node.left.val # 回溯if node.right:div -= node.right.valif self.traversal(node.right, div): # 右return Truediv += node.right.val # 回溯return False精简写法,隐藏回溯
class Solution2:def hasPathSum(self, root: TreeNode, targetSum: int) -> bool:if not root:return Falseif not root.left and not root.right:if targetSum == root.val:return Trueelse:return Falsereturn self.hasPathSum(root.left, targetSum - root.val) or self.hasPathSum(root.right, targetSum - root.val)113.路径总和 II
题目链接:113. 路径总和 II - 力扣(LeetCode)
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例: 给定二叉树[5,4,8,11,None,13,4,7,2,None,None,5,1],以及目标和 sum = 22,
返回:[
[5,4,11,2],
[5,8,4,5]
]
思路
DFS深度优先遍历算法,前序遍历,每次遍历采用目标值去减当前节点,
一旦出现差值div为0,可以判断是否是叶子节点,是叶子节点则保存当前节点
如果遍历到叶子节点,div != 0 继续遍历
这题也要注意回溯过程
class Solution:def PathSum(self, root: TreeNode, targetSum: int) -> list[list[int]]:self.result = []if not root:return []div = targetSum - root.valpath = [root.val]self.traversal(root, path, div)return self.resultdef traversal(self, node, path, div):# 终止条件if not node.left and not node.right :if div == 0:self.result.append(path.copy())returnif node.left:div -= node.left.valpath.append(node.left.val)self.traversal(node.left, path, div) # 左div += node.left.val # 回溯path.pop()if node.right:div -= node.right.valpath.append(node.right.val)self.traversal(node.right, path, div) # 右div += node.right.val # 回溯path.pop()上面的代码中,有一个地方,要格外注意:当判断为叶子节点,且div为0时,我需要添加当前路径到列表中。
这里产生了一个问题,问题出现在将 path 添加到 self.result 中时,实际上添加的是 path 的引用,而不是 path 的副本。这意味着当 path 发生变化时,已经添加到 self.result 中的路径也会随之变化。
解决这个问题的方法是,将 path 添加到 self.result 中时,添加 path 的副本而不是直接添加 path。这样就不会受到 path 变化的影响。我后来使用 path.copy() 来创建 path 的副本。也可以用path[:]

上面的代码好理解,但写的并不好,紧接进行改进
1.避免全局变量:目前代码中使用了 self.result 作为全局变量来存储结果。虽然这种方法可以工作,但不推荐使用全局变量,因为它会增加代码的复杂性和维护成本。相反,可以将结果作为函数的返回值,这样可以使代码更加清晰和可维护。
2.递归中改成隐式回溯:在递归函数中不再修改传递的参数,而是在函数内部创建局部变量来处理路径和目标值。这样可以减少代码的复杂性,并降低出错的风险。
3.使用列表推导式简化代码:在遍历左右子树时,可以使用列表推导式来简化代码。这样可以使代码更加简洁和易读。
class Solution2:def PathSum(self, root: TreeNode, targetSum: int) -> list[list[int]]:result = []if not root:return resultself.traversal(root, [root.val], targetSum - root.val, result)return resultdef traversal(self, node, path: list[int], target, result):# 终止条件if not node.left and not node.right and target == 0:result.append(path.copy())return# 左子树if node.left:self.traversal(node.left, path+[node.left.val], target - node.left.val, result)# 右子树if node.right:self.traversal(node.right, path+[node.right.val], target - node.right.val, result)
在上面代码中,我企图将路径path与差值div参数均隐藏回溯
 div隐藏回溯没有什么问题,路径隐藏回溯时,我就很常规的将path.append(node.left.val)作为参数参入,存在一个潜在的问题。
div隐藏回溯没有什么问题,路径隐藏回溯时,我就很常规的将path.append(node.left.val)作为参数参入,存在一个潜在的问题。
在Python中,list.append() 方法会直接修改原列表,并且返回值为 None,因此我在递归调用时实际上传递的是 None,而不是修改后的 path。这可能导致程序运行时出现错误。
后来我使用 path + [node.left.val] 的方式创建新的路径,在递归调用时传递这个新的路径,而不是直接修改原路径 path。
106.从中序与后序遍历序列构造二叉树
题目链接:
106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
根据一棵树的中序遍历与后序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出中序遍历 inorder = [9,3,15,20,7] 后序遍历 postorder = [9,15,7,20,3]
返回二叉树[3,9,20,None,None,15,7]
文章讲解:代码随想录 (programmercarl.com)
视频讲解:坑很多!来看看你掉过几次坑 | LeetCode:106.从中序与后序遍历序列构造二叉树哔哩哔哩bilibili
思路:
中:左中右 后:左右中
核心:后序遍历列表中,最后一个肯定是中节点(也是根节点),通过这个中节点去拆分中序遍历列表的左右区间
1.后序数组为0,空节
2.后序数组最后一个元素为节点元素
3.寻找中序数组位置作切割点
4.切中序数组
5.切后序数组
6.递归处理中后序中的左右区间
7.返回答案
class Solution:def buildTree(self, inorder: list[int], postorder: list[int]) -> Optional[TreeNode]:# todo 1.后序数组为0,空节点if not postorder:return# todo 2.后序数组最后一个元素为节点元素node = TreeNode(postorder[-1])# todo 3.寻找中序数组位置作切割点index = inorder.index(node.val)# todo 4.切中序数组left_inorder = inorder[:index]right_inorder = inorder[index+1:]# todo 5.切后序数组size = len(left_inorder)left_postorder = postorder[:size]right_postorder = postorder[size:len(postorder)-1]# todo 6.递归处理中后序中的左右区间node.left = self.buildTree(left_inorder,left_postorder)node.right = self.buildTree(right_inorder,right_postorder)# todo 7.返回答案return node
105.从前序与中序遍历序列构造二叉树
题目链接:
105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
思路:
中:左中右 前:中左右
1.前序数组为0,空节点
2.前序数组第一个元素为节点元素
3.寻找中序数组位置作切割点
4.切中序数组
5.切前序数组
6.递归处理前中序中的左右区间
7.返回答案
class Solution:def buildTree(self, preorder: list[int], inorder: list[int]) -> Optional[TreeNode]:# todo 1.前序数组为0,空节点if not preorder:return# todo 2.前序数组第一个元素为节点元素node = TreeNode(preorder[0])# todo 3.寻找中序数组位置作切割点index = inorder.index(preorder[0])# todo 4.切中序数组left_inorder = inorder[:index]right_inorder = inorder[index+1:]# todo 5.切前序数组size = len(left_inorder)left_preorder = preorder[1:size+1]right_preorder = preorder[size+1:]# todo 6.递归处理前中序中的左右区间node.left = self.buildTree(left_preorder,left_inorder)node.right = self.buildTree(right_preorder,right_inorder)# todo 7.返回答案return node
感想:
这两题不好想,首先要知道前中后序遍历的顺序
前序:中左右 中序:左中右 后序:左右中
前中序与后中序都能确定唯一的二叉树,但是前后序不行
举个例子
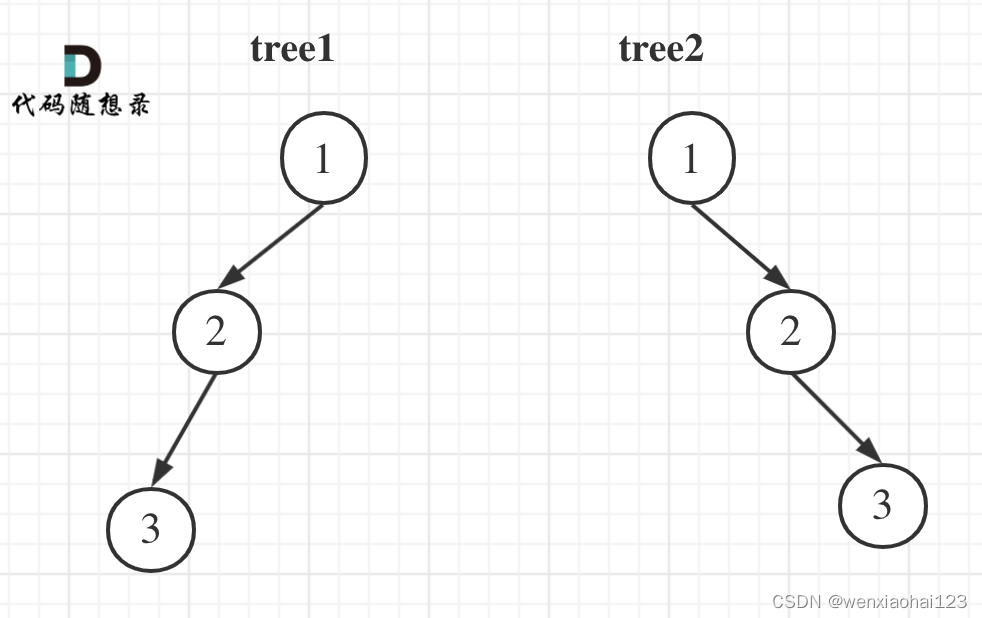
tree1 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
tree2 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
那么tree1 和 tree2 的前序和后序完全相同,这是一棵树么,很明显是两棵树!
所以前序和后序不能唯一确定一棵二叉树
为什么非得需要中序呢
这也是解这题的核心。我们可以由前后序列表知道中间节点的位置,正是因为中序遍历是左中右,所以我们继而用这个中节点去拆分中序列表中左右子树区间,从而能进行递归。
如果我们拿到的是前后序,前序为中左右,后序为左右中国,及时知道中间节点也无法去拆分左右子树区间。所以我们能由前中序遍历或中后序遍历确定唯一的二叉树