目录

最长递增子序列 

 摆动序列

 最长递增子序列的个数

 最长数对链

 最长定差子序列

 最长的斐波那契子序列的长度

 最长等差数列

等差数列划分 II - 子序列 

---

最长递增子序列 

300. 最长递增子序列

 子数组是连续的，子序列可以不连续，那么就要去[0, i - 1] 区间找

参考代码

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n, 1);int ret = 1;for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){if(nums[i] > nums[j])dp[i] = max(dp[i], dp[j] + 1);}ret = max(ret, dp[i]);}return ret;}
};

 摆动序列

 376. 摆动序列

错误： g[i] = max(g[i], f[j] + 1);这个地方写错成f[i]，导致逻辑错误

参考代码

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int n = nums.size();vector<int> f(n, 1), g(n, 1);int ret = 1;for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){if(nums[j] < nums[i]) f[i] = max(f[i], g[j] + 1);else if(nums[j] > nums[i]) g[i] = max(g[i], f[j] + 1);}ret = max(ret, max(f[i], g[i]));}return ret;}
};

 最长递增子序列的个数

673. 最长递增子序列的个数 ☆☆☆☆☆

逻辑其实差不多，我们需要用len来更新count，如果只表示一个count的话没有len，没法更新count；只有在nums[j] < nums[i] 的时候才能操作，这是递增的基本条件；然后通过长度来更新；大于自然要重置，等于则延续count[j]；通过for j 循环找出 i 位置为结尾的最长长度和最大个数

参考代码

class Solution {
public:int findNumberOfLIS(vector<int>& nums) {int n = nums.size();vector<int> len(n, 1), count(n, 1);int maxlen = 1, retcount = 1;for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){if(nums[j] < nums[i]){if(len[j] + 1 == len[i]) count[i] += count[j];else if(len[j] + 1 > len[i])len[i] = len[j] + 1, count[i] = count[j];}}if(len[i] > maxlen)maxlen = len[i], retcount = count[i];else if(len[i] == maxlen)retcount += count[i];}return retcount;}
};

 最长数对链

646. 最长数对链

 去[0,  i - 1] 里面找符合条件的，再比较

参考代码

class Solution {
public:int findLongestChain(vector<vector<int>>& pairs) {int n = pairs.size();sort(pairs.begin(), pairs.end());vector<int> dp(n, 1);int ret = 1;for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){if(pairs[j][1] < pairs[i][0])dp[i] = max(dp[i], dp[j] + 1);}ret = max(ret, dp[i]);}return ret;}
};

 最长定差子序列

1218. 最长定差子序列

 最开始，老样子n方，但是发现超时；

class Solution5_1 {
public:int longestSubsequence(vector<int>& arr, int difference) {int n = arr.size();vector<int> dp(n, 1);int ret = 1;for (int i = 1; i < n; i++){for (int j = 0; j < i; j++){if (arr[j] + difference == arr[i]) dp[i] = max(dp[i], dp[j] + 1);}ret = max(ret, dp[i]);}return ret;}
};

然后发现只要找最后一个倒找，找到最后一个满足差值的就行；后面才发现，如果一个数据很长而且都满足条件的很少，那么这个时候优化就没有用了，

class Solution5_2 {
public:int longestSubsequence(vector<int>& arr, int difference) {int n = arr.size();vector<int> dp(n, 1);int ret = 1;for (int i = 1; i < n; i++){for (int j = i - 1; j >= 0; j--){if (arr[j] + difference == arr[i]){dp[i] = dp[j] + 1;break;}}ret = max(ret, dp[i]);}return ret;}
};

 所以我们采用hash<元素, 满足条件的个数>来映射

参考代码

class Solution {
public:int longestSubsequence(vector<int>& arr, int difference) {unordered_map<int, int> hash;int n = arr.size(), ret = 1;hash[arr[0]] = 1;for(int i = 1; i < n; i++){hash[arr[i]] = hash[arr[i] - difference] + 1;ret = max(ret, hash[arr[i]]);}return ret;}
};

 最长的斐波那契子序列的长度

873. 最长的斐波那契子序列的长度

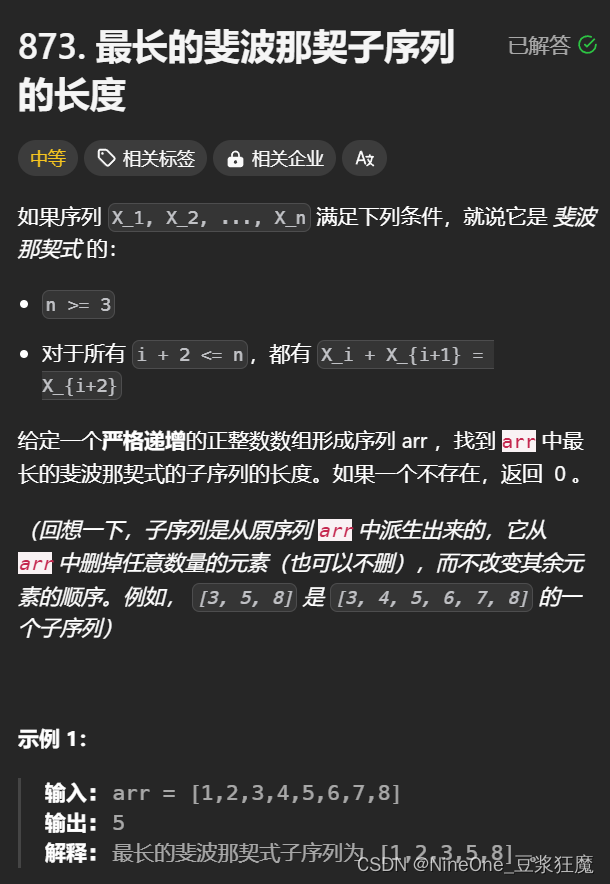
 如果是一维的状态表示：以i位置为结尾的最长斐波那契序列的长度，那么它的更新条件就要前面两个数，又要遍历两遍，但也不对，没法通过前面的状态来改变当前位置的状态；

所以用结尾两个位置来锁定这个斐波那契序列；自然就是二维dp

且是严格递增，hash可以直接全写出来(也可以一步一步定义)，且是<int , int> 每个元素只有一个对应的下标

注意：最后一步 oj题没有这时候只会报错，

参考代码

class Solution {
public:int lenLongestFibSubseq(vector<int>& arr) {int n = arr.size();vector<vector<int>> dp(n, vector<int>(n, 2));unordered_map<int, int> hash;for(int i = 0; i < n; i++)hash[arr[i]] = i;int ret = 2;for(int j = 2; j < n; j++){for(int i = 1; i < j; i++){int num = arr[j] - arr[i];if(hash.count(num) && hash[num] < i)dp[i][j] = dp[hash[num]][i] + 1;ret = max(ret, dp[i][j]);}}return ret < 3 ? 0 : ret;}
};

一步步定义参考代码 

class Solution {
public:int lenLongestFibSubseq(vector<int>& arr) {int n = arr.size();vector<vector<int>> dp(n, vector<int>(n, 2));unordered_map<int, int> hash;// for(int i = 0; i < n; i++)//     hash[arr[i]] = i;hash[arr[0]] = 0;int ret = 2;for (int i = 1; i < n - 1; i++){for (int j = i + 1; j < n; j++){int num = arr[j] - arr[i];if (hash.count(num) && hash[num] < i)dp[i][j] = dp[hash[num]][i] + 1;ret = max(ret, dp[i][j]);}hash[arr[i]] = i;}return ret < 3 ? 0 : ret;}
};

 最长等差数列

1027. 最长等差数列

 

以为我们需要元素对应的下标，所以用哈希表，

第二，这题并不是严格递增，那就是很可能会有相同的数，如果一次定义完哈希值，那么相同元素的下标就会用后面的那个，但是也可以定义为<int, vector<int>>

其三：每一次的 i  j 结尾都是不同的，所以ret必须要放在第二层循环里

注意 ret = 2, 题目是length >= 2 ，且两个数也被认为是构成等差数列

代码如下

class Solution {
public:int longestArithSeqLength(vector<int>& nums) {int n = nums.size();vector<vector<int>> dp(n, vector<int>(n, 2));int ret = 2;unordered_map<int, vector<int>> hash;for(int i = 0; i < n; i++)hash[nums[i]].push_back(i);for(int j = 2; j < n; j++){for(int i = 1; i < j; i++){int num = 2 * nums[i] - nums[j];// if(hash.count(num) && hash[num] < i)//不能这么写了因为hash[num]是vector<int>if(hash.count(num))for(auto e : hash[num])if(e < i)dp[i][j] = max(dp[i][j], dp[e][i] + 1);ret = max(ret, dp[i][j]);}}return ret;}
};

 和 -> 最长定差子序列 想法类似，num只要找最接近 i 的就行,可以理解为覆盖掉原来的距离 i 较远元素的下标

参考代码

class Solution {
public:int longestArithSeqLength(vector<int>& nums) {int n = nums.size();vector<vector<int>> dp(n, vector<int>(n, 2));int ret = 2;unordered_map<int, int> hash;hash[nums[0]] = 0;for(int i = 1; i < n - 1; i++){for(int j = i + 1; j < n; j++){int num = 2 * nums[i] - nums[j];if(hash.count(num) && hash[num] < i)dp[i][j] = dp[hash[num]][i] + 1;ret = max(ret, dp[i][j]);}hash[nums[i]] = i;}return ret;}
};

等差数列划分 II - 子序列 

 446. 等差数列划分 II - 子序列

 思路： 题目求的是个数，那么dp表要初始化成0，既然是子序列  个数 那么就是满足条件的所有下标（e），这里不能覆盖下标，要找到所有下标，所以hash是int 和vector<int> 对应,

两个i  j   for的顺序只对覆盖hash有影响作用

参考代码

class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();vector<vector<int>> dp(n, vector<int>(n));unordered_map<long long, vector<int>> hash;for(int i = 0; i < n; i++)hash[nums[i]].push_back(i);int ret = 0;for(int i = 1; i < n - 1; i++){for(int j = i + 1; j < n; j++){long long num = (long long)2 * nums[i] - nums[j];if(hash.count(num))for(auto e : hash[num])if(e < i)dp[i][j] += dp[e][i] + 1;ret += dp[i][j];}}return ret;}
};