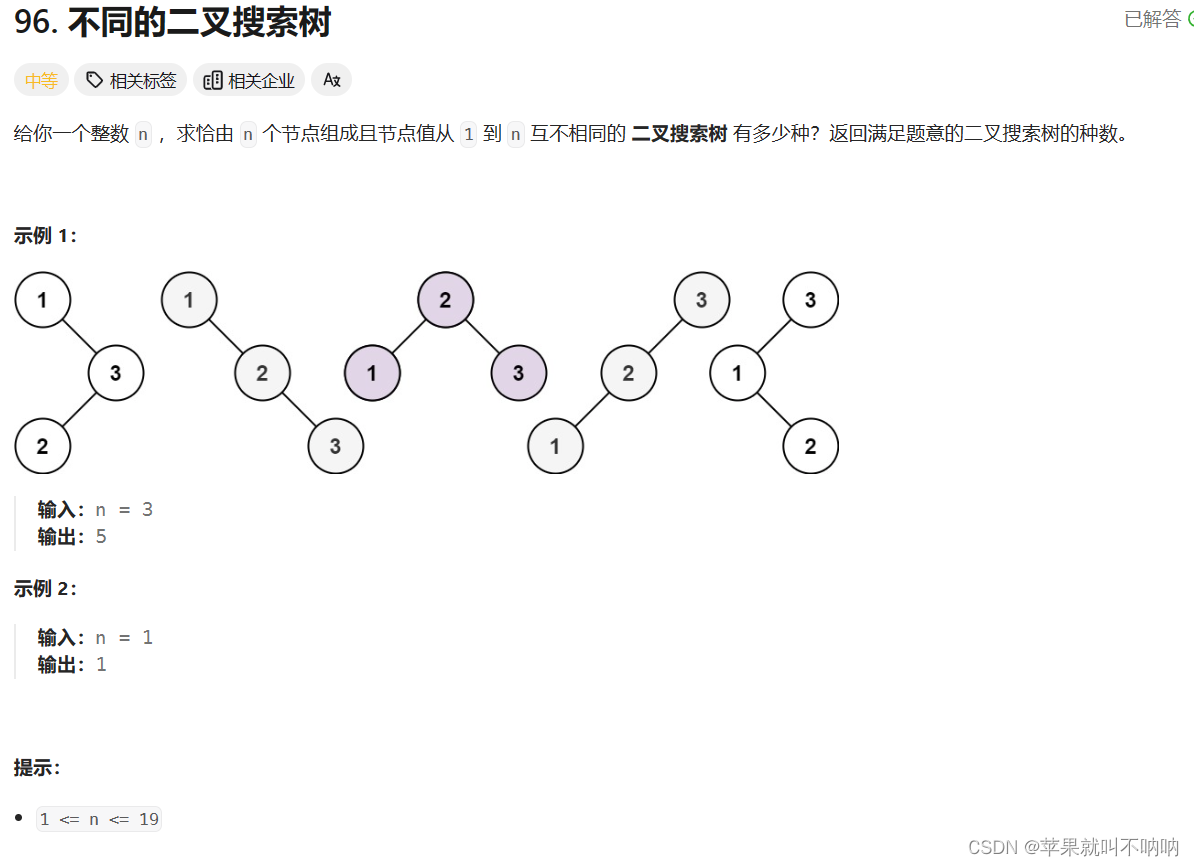
---------------🎈🎈96. 不同的二叉搜索树 题目链接🎈🎈-------------------

动态规划

😒: 我的代码实现============>

动规五部曲

✒️确定dp数组以及下标的含义

dp[i] ： i个不同元素节点组成的二叉搜索树的个数为dp[i]

✒️确定递推公式

dp[i] = dp[i] + dp[j - 1] * dp[i - j] ，
j-1 : 以 j 为头结点左子树节点数量，i-j : 以j为头结点右子树节点数量

举例
dp[3] = 元素1为头结点的搜索树的数量 + 元素2为头结点的搜索树的数量 + 元素3为头结点的搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 × 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 × 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 × 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] × dp[0] + dp[1] × dp[1] + dp[0] × dp[2]

✒️dp数组初始化

dp[0] = 1, dp[1] = 1, dp[2] = 2

✒️确定遍历顺序

遍历节点数，从递归公式：dp[i] += dp[j - 1] * dp[i - j]可以看出，节点数为i的状态是依靠 i之前节点数的状态。

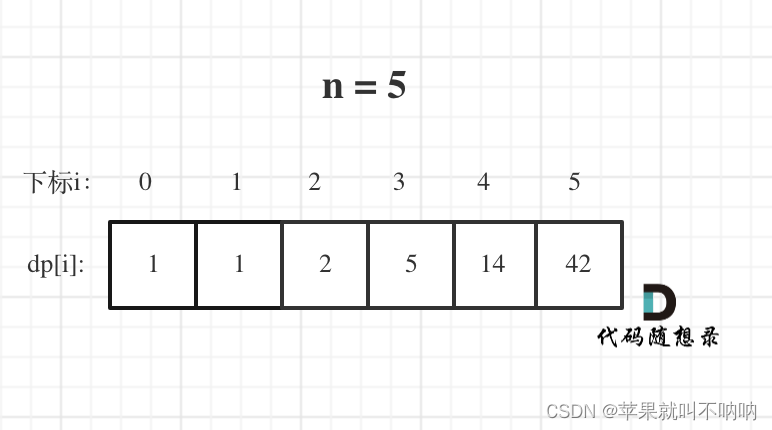
✒️举例推导dp数组

时间复杂度O(N)
空间复杂度O(N)

📘代码

class Solution {public int numTrees(int n) {if(n == 1) return 1;int[] dp = new int[n+1];dp[0] = 1;dp[1] = 1;dp[2] = 2;for(int i = 3; i<=n; i++){for(int j = 0; j < i; j++){dp[i] += dp[j]*dp[i-j-1];}}return dp[n];}
}         

卡特兰数