---

题目

链接: link

思路：简单递归 > 动态规划

这题类似于斐波那契数列的算法，结果其实就是到达前一步和到达前两步的方法之和，一直递归到n=1和n=2时就行了，但是这种算法有个缺点就是递归的耗时太长了容易报错

int climbStairs(int n) {if (n == 1)return 1;else if (n == 2)return 2;elsereturn climbStairs(n - 1) + climbStairs(n - 2);
}

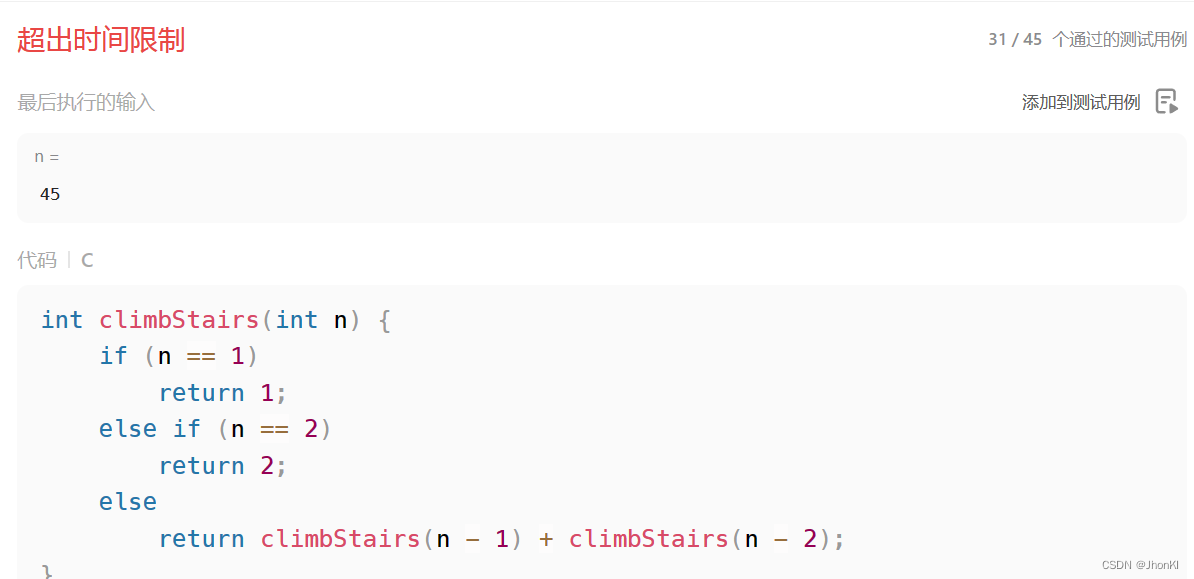
所以这里我们可以尝试使用动态规划的方法，就是说这里我们是知道目标数的，所以我们可以直接利用for循环从1和2开始一直循环下去，使 f(n) = f(n-1) + f(n-2) 下去，比上面的递归的空间复杂度就小了很多，只有O(n)，同时因为没有额外创建循环空间，所以最后空间复杂度是O(1)

int climbStairs(int n) {int p = 0;int q = 0;int s = 1;for (int i = 1; i <= n; i++) {p = q;q = s;s = p + q;}return s;
}

其实这里还可以用数学的方法做，但是有带你复杂就不说了，有兴趣可以去力扣官方解题思路里看看。