一、机器学习概述
第1关机器学习概述
B AD B BC

第2关常见分类算法
#编码方式encoding=utf8from sklearn.neighbors import KNeighborsClassifierdef knn(train_data,train_label,test_data):'''input:train_data用来训练的数据train_label用来训练的标签test_data用来测试的数据'''#********* Begin *********#开始填补空缺处代码knn = KNeighborsClassifier()#利用训练数据与标签对模型进行训练knn.fit(train_data, train_label)#对测试数据类别进行预测predict = knn.predict(test_data)#********* End *********#结束填补位置return predict第3关常见回归算法
#编码方式encoding=utf8
from sklearn.linear_model import LinearRegressiondef lr(train_data,train_label,test_data):'''input:train_data用来训练的数据train_label用来训练的标签test_data用来测试的数据'''#********* Begin *********#开始填补空缺处代码lr = LinearRegression()#利用已知数据与标签对模型进行训练lr.fit(train_data, train_label)#对未知数据进行预测predict = lr.predict(test_data)#********* End *********#return predict第4关常见聚类算法
from sklearn.cluster import KMeans def kmeans(data):'''input:data需要进行聚类的数据'''# 假设我们想要将数据聚成3类,这个数字可以根据实际情况调整kmeans = KMeans(n_clusters=3, random_state=888)# 使用fit_predict一步完成模型训练和预测predict = kmeans.fit_predict(data)return predict # 返回聚类结果第五关实现KNN算法
import numpy as npclass kNNClassifier(object):def __init__(self, k):'''初始化函数:param k:kNN算法中的k'''self.k = k# 用来存放训练数据,类型为ndarrayself.train_feature = None# 用来存放训练标签,类型为ndarrayself.train_label = Nonedef fit(self, feature, label):'''kNN算法的训练过程:param feature: 训练集数据,类型为ndarray:param label: 训练集标签,类型为ndarray:return: 无返回'''# 将传入的训练数据和标签保存在对象内部,以便后续的预测使用self.train_feature = np.array(feature)self.train_label = np.array(label)def predict(self, feature):'''kNN算法的预测过程:param feature: 测试集数据,类型为ndarray:return: 预测结果,类型为ndarray或list'''def _predict(test_data):# 计算测试数据与所有训练数据之间的欧氏距离distances = [np.sqrt(np.sum((test_data - vec) ** 2)) for vec in self.train_feature]# 获取距离最近的训练数据的索引nearest = np.argsort(distances)# 选取最近的 k 个邻居topK = [self.train_label[i] for i in nearest[:self.k]]votes = {} # 用字典来记录每个类别的投票数result = Nonemax_count = 0 # 用来记录最高票数for label in topK:if label in votes:votes[label] += 1else:votes[label] = 1# 更新最高票数和对应的类别if votes[label] > max_count:max_count = votes[label]result = labelreturn result# 对测试集中的每个数据进行预测predict_result = [_predict(test_data) for test_data in feature]return predict_result二、机器学习—线性回归
第1关简单线性回归与多元线性回归
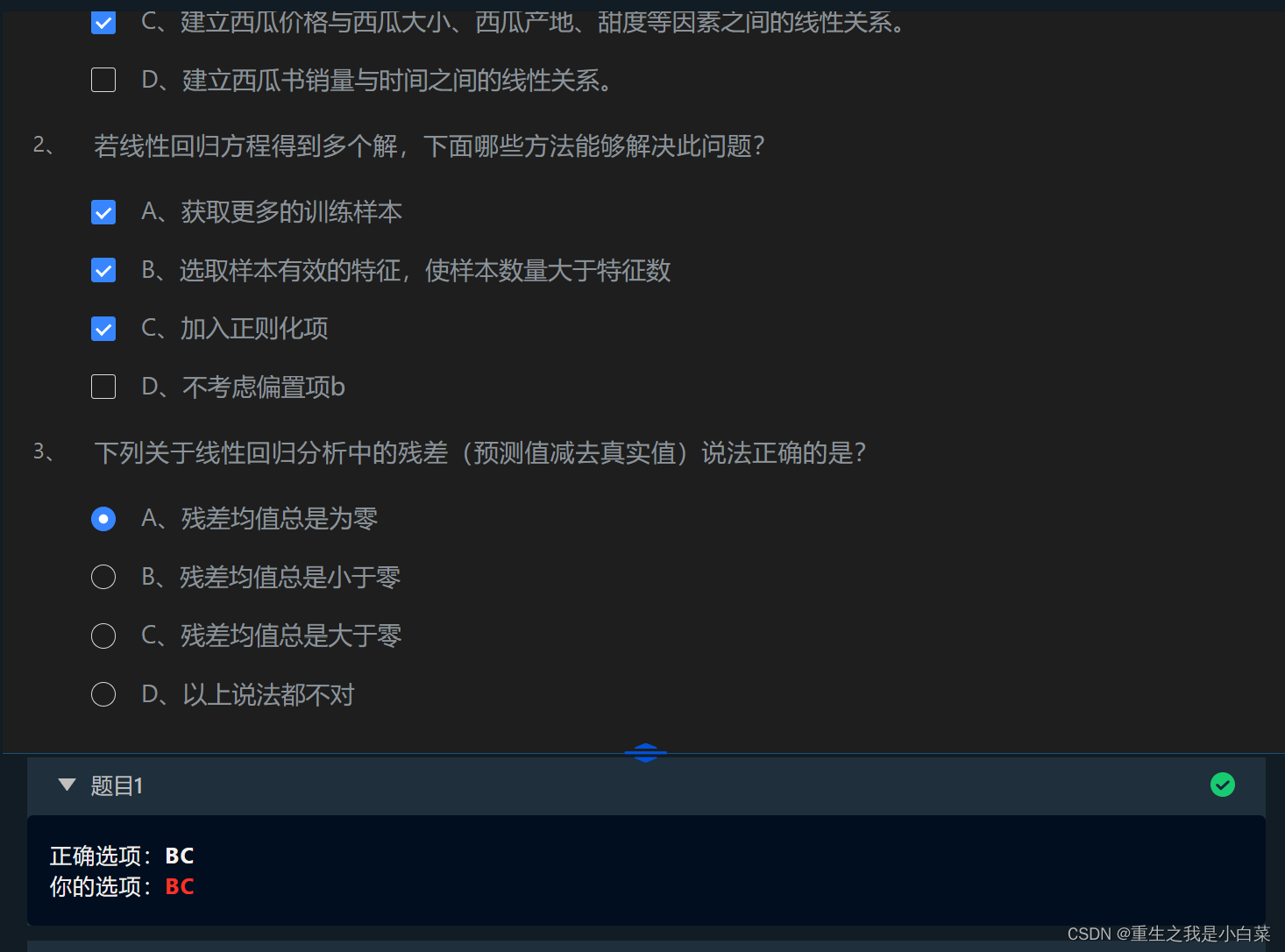
第2关线性回归的正规方程解
import numpy as npdef mse_score(y_predict, y_test):'''input:y_predict(ndarray):预测值y_test(ndarray):真实值output:mse(float):mse损失函数值'''# 计算均方误差mse = np.mean((y_predict - y_test) ** 2)return mseclass LinearRegression:def __init__(self):'''初始化线性回归模型'''self.theta = Nonedef fit_normal(self, train_data, train_label):'''input:train_data(ndarray):训练样本train_label(ndarray):训练标签'''# 在训练数据前添加一列1,对应theta0X_b = np.hstack([np.ones((len(train_data), 1)), train_data])# 使用正规方程求解thetaself.theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(train_label)def predict(self, test_data):'''input:test_data(ndarray):测试样本'''# 在测试数据前添加一列1,对应theta0X_b = np.hstack([np.ones((len(test_data), 1)), test_data])# 使用模型进行预测y_predict = X_b.dot(self.theta)return y_predict第3关衡量线性回归的性能指标
import numpy as np#mse
def mse_score(y_predict, y_test):mse = np.mean((y_predict - y_test) ** 2)return mse#r2
def r2_score(y_predict, y_test):'''input:y_predict(ndarray):预测值y_test(ndarray):真实值output:r2(float):r2值'''# 计算R2分数ss_total = np.sum((y_test - np.mean(y_test)) ** 2)ss_residual = np.sum((y_test - y_predict) ** 2)r2 = 1 - (ss_residual / ss_total)return r2class LinearRegression:def __init__(self):'''初始化线性回归模型'''self.theta = Nonedef fit_normal(self, train_data, train_label):'''input:train_data(ndarray):训练样本train_label(ndarray):训练标签'''# 在训练数据前添加一列1,对应theta0X_b = np.hstack([np.ones((len(train_data), 1)), train_data])# 使用正规方程求解thetaself.theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(train_label)return selfdef predict(self, test_data):'''input:test_data(ndarray):测试样本'''# 在测试数据前添加一列1,对应theta0X_b = np.hstack([np.ones((len(test_data), 1)), test_data])# 使用模型进行预测y_predict = X_b.dot(self.theta)return y_predict第4关scikit-learn线性回归实践 - 波斯顿房价预测
#encoding=utf8
#encoding=utf8#********* Begin *********#
import pandas as pd
from sklearn.linear_model import LinearRegression# 获取训练数据
train_data = pd.read_csv('./step3/train_data.csv')# 获取训练标签
train_label = pd.read_csv('./step3/train_label.csv')
train_label = train_label['target']# 获取测试数据
test_data = pd.read_csv('./step3/test_data.csv')lr = LinearRegression()# 训练模型
lr.fit(train_data, train_label)# 获取预测标签
predict = lr.predict(test_data)# 将预测标签写入csv
df = pd.DataFrame({'result': predict})
df.to_csv('./step3/result.csv', index=False)#********* End *********#三、机器学习 --- 模型评估、选择与验证
第1关:为什么要有训练集与测试集
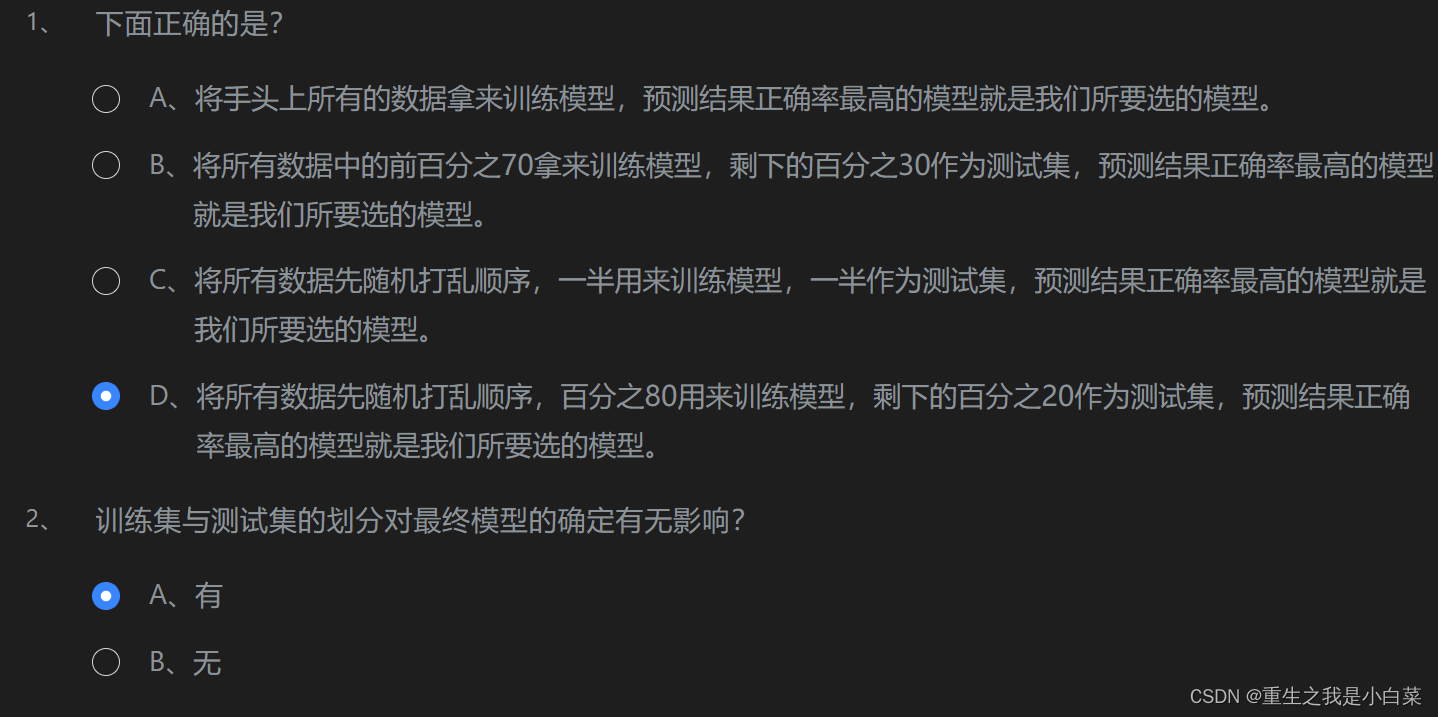
第2关欠拟合与过拟合

第3关偏差与方差

第4关验证集与交叉验证
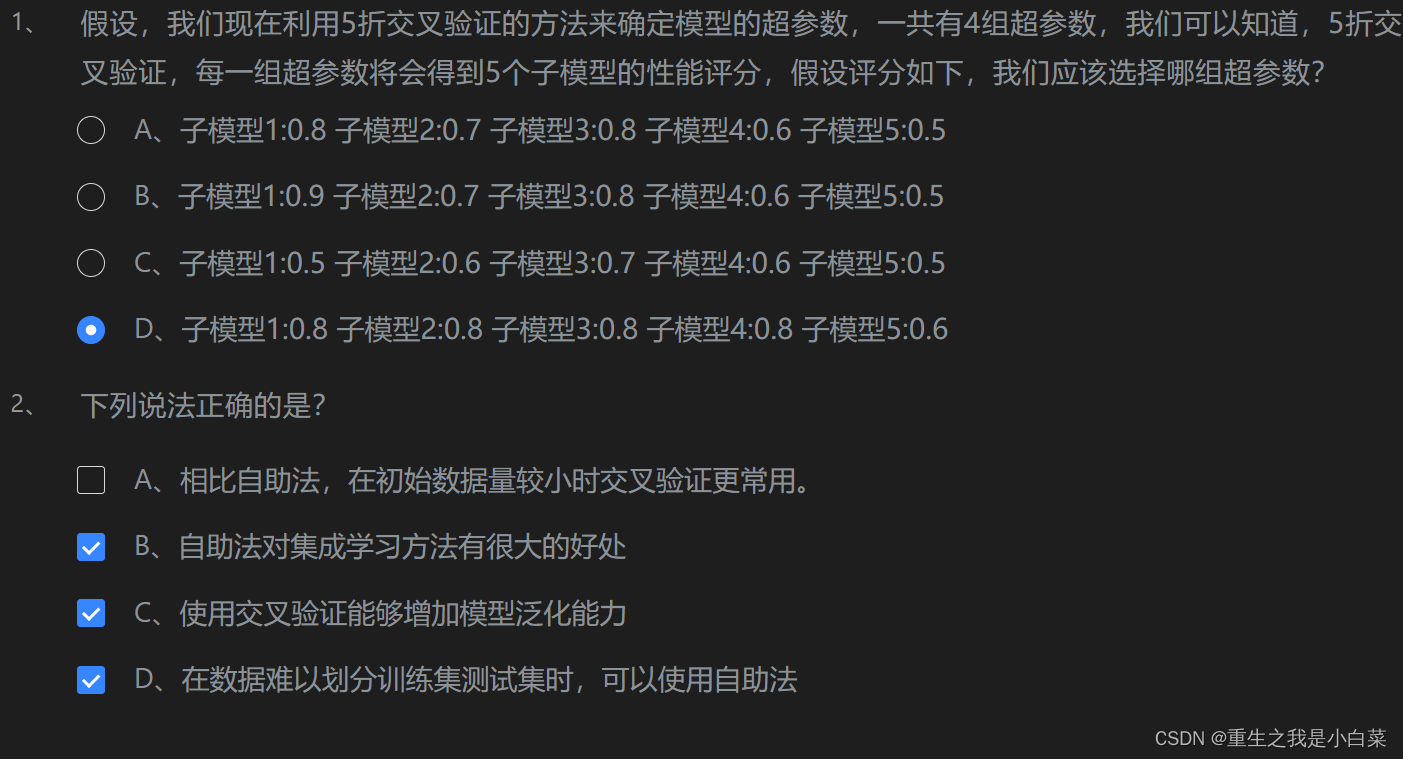
第5关衡量回归性能指标
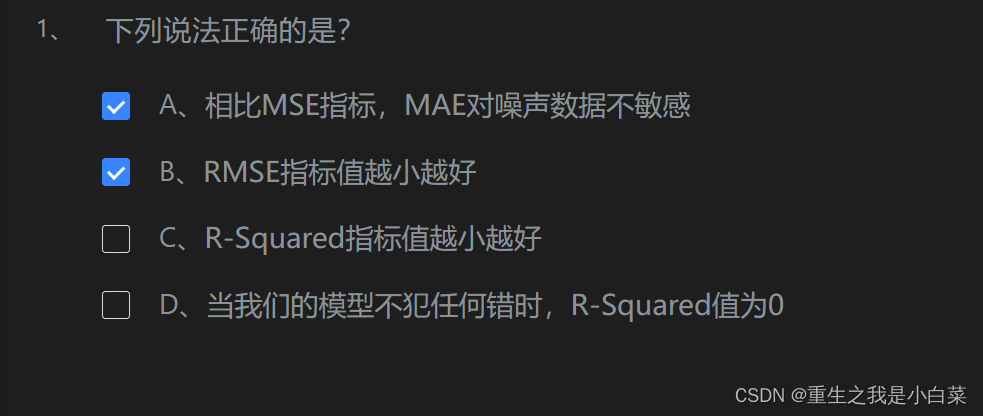
第6关准确度的陷阱与混淆矩阵
import numpy as npdef confusion_matrix(y_true, y_predict):'''构建二分类的混淆矩阵,并将其返回:param y_true: 真实类别,类型为ndarray:param y_predict: 预测类别,类型为ndarray:return: shape为(2, 2)的ndarray'''# 定义计算混淆矩阵各元素的函数def TN(y_true, y_predict):return np.sum((y_true == 0) & (y_predict == 0))def FP(y_true, y_predict):return np.sum((y_true == 0) & (y_predict == 1))def FN(y_true, y_predict):return np.sum((y_true == 1) & (y_predict == 0))def TP(y_true, y_predict):return np.sum((y_true == 1) & (y_predict == 1))# 构建并返回混淆矩阵return np.array([[TN(y_true, y_predict), FP(y_true, y_predict)],[FN(y_true, y_predict), TP(y_true, y_predict)]])第7关精准率与召回率
import numpy as npdef precision_score(y_true, y_predict):'''计算精准率并返回:param y_true: 真实类别,类型为ndarray:param y_predict: 预测类别,类型为ndarray:return: 精准率,类型为float'''# 定义计算真正例(TP)和假正例(FP)的函数def TP(y_true, y_predict):return np.sum((y_true == 1) & (y_predict == 1))def FP(y_true, y_predict):return np.sum((y_true == 0) & (y_predict == 1))# 计算TP和FPtp = TP(y_true, y_predict)fp = FP(y_true, y_predict)# 计算精准率并返回try:return tp / (tp + fp)except:return 0.0def recall_score(y_true, y_predict):'''计算召回率并返回:param y_true: 真实类别,类型为ndarray:param y_predict: 预测类别,类型为ndarray:return: 召回率,类型为float'''# 定义计算真正例(TP)和假负例(FN)的函数def FN(y_true, y_predict):return np.sum((y_true == 1) & (y_predict == 0))def TP(y_true, y_predict):return np.sum((y_true == 1) & (y_predict == 1))# 计算TP和FNtp = TP(y_true, y_predict)fn = FN(y_true, y_predict)# 计算召回率并返回try:return tp / (tp + fn)except:return 0.0第8关F1 Score
import numpy as npdef f1_score(precision, recall):'''计算模型的F1分数并返回:param precision: 模型的精准率,类型为float:param recall: 模型的召回率,类型为float:return: 模型的f1 score,类型为float'''# 计算F1分数try:return 2 * precision * recall / (precision + recall)except:return 0.0第9关ROC曲线与AUC
import numpy as npdef calAUC(prob, labels):'''计算AUC并返回:param prob: 模型预测样本为Positive的概率列表,类型为ndarray:param labels: 样本的真实类别列表,其中1表示Positive,0表示Negtive,类型为ndarray:return: AUC,类型为float'''# 将概率和标签组合并按概率排序f = list(zip(prob, labels))rank = [values2 for values1, values2 in sorted(f, key=lambda x: x[0])]# 获取正样本的排名列表rankList = [i + 1 for i in range(len(rank)) if rank[i] == 1]# 计算正负样本的数量posNum = sum(labels)negNum = len(labels) - posNum# 根据公式计算AUCauc = (sum(rankList) - (posNum * (posNum + 1)) / 2) / (posNum * negNum)return auc第10关sklearn中的分类性能指标
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_scoredef classification_performance(y_true, y_pred, y_prob):'''返回准确度、精准率、召回率、f1 Score和AUC:param y_true: 样本的真实类别,类型为`ndarray`:param y_pred: 模型预测出的类别,类型为`ndarray`:param y_prob: 模型预测样本为`Positive`的概率,类型为`ndarray`:return: 准确度、精准率、召回率、f1 Score和AUC,类型为tuple'''# 计算并返回各种性能指标return accuracy_score(y_true, y_pred), precision_score(y_true, y_pred), recall_score(y_true, y_pred), f1_score(y_true, y_pred), roc_auc_score(y_true, y_prob)四、聚类性能评估指标
第1关外部指标
import numpy as npdef calc_JC(y_true, y_pred):'''计算并返回JC系数:param y_true: 参考模型给出的簇,类型为ndarray:param y_pred: 聚类模型给出的簇,类型为ndarray:return: JC系数'''def a(y_true, y_pred):result = 0for i in range(len(y_true)):for j in range(len(y_pred)):if i < j:if y_true[i] == y_true[j] and y_pred[i] == y_pred[j]:result += 1return resultdef b(y_true, y_pred):result = 0for i in range(len(y_true)):for j in range(len(y_pred)):if i < j:if y_true[i] != y_true[j] and y_pred[i] == y_pred[j]:result += 1return resultdef c(y_true, y_pred):result = 0for i in range(len(y_true)):for j in range(len(y_pred)):if i < j:if y_true[i] == y_true[j] and y_pred[i] != y_pred[j]:result += 1return resultreturn a(y_true, y_pred) / (a(y_true, y_pred) + b(y_true, y_pred) + c(y_true, y_pred))def calc_FM(y_true, y_pred):'''计算并返回FM指数:param y_true: 参考模型给出的簇,类型为ndarray:param y_pred: 聚类模型给出的簇,类型为ndarray:return: FM指数'''def a(y_true, y_pred):result = 0for i in range(len(y_true)):for j in range(len(y_pred)):if i < j:if y_true[i] == y_true[j] and y_pred[i] == y_pred[j]:result += 1return resultdef b(y_true, y_pred):result = 0for i in range(len(y_true)):for j in range(len(y_pred)):if i < j:if y_true[i] != y_true[j] and y_pred[i] == y_pred[j]:result += 1return resultdef c(y_true, y_pred):result = 0for i in range(len(y_true)):for j in range(len(y_pred)):if i < j:if y_true[i] == y_true[j] and y_pred[i] != y_pred[j]:result += 1return resultreturn a(y_true, y_pred) / np.sqrt((a(y_true, y_pred) + b(y_true, y_pred)) * (a(y_true, y_pred) + c(y_true, y_pred)))def calc_Rand(y_true, y_pred):'''计算并返回Rand指数:param y_true: 参考模型给出的簇,类型为ndarray:param y_pred: 聚类模型给出的簇,类型为ndarray:return: Rand指数'''def a(y_true, y_pred):result = 0for i in range(len(y_true)):for j in range(len(y_pred)):if i < j:if y_true[i] == y_true[j] and y_pred[i] == y_pred[j]:result += 1return resultdef d(y_true, y_pred):result = 0for i in range(len(y_true)):for j in range(len(y_pred)):if i < j:if y_true[i] != y_true[j] and y_pred[i] != y_pred[j]:result += 1return resultm = len(y_true)return (2 * (a(y_true, y_pred) + d(y_true, y_pred))) / (m * (m - 1))第2关内部指标
import numpy as npdef calc_DBI(feature, pred):'''计算并返回DB指数:param feature: 待聚类数据的特征,类型为`ndarray`:param pred: 聚类后数据所对应的簇,类型为`ndarray`:return: DB指数'''#********* Begin *********#label_set = np.unique(pred)mu = {}label_count = {}#计算簇的中点for label in label_set:mu[label] = np.zeros([len(feature[0])])label_count[label] = 0for i in range(len(pred)):mu[pred[i]] += feature[i]label_count[pred[i]] += 1for key in mu.keys():mu[key] /= label_count[key]#算数据到中心点的平均距离avg_d = {}for label in label_set:avg_d[label] = 0for i in range(len(pred)):avg_d[pred[i]] += np.sqrt(np.sum(np.square(feature[i] - mu[pred[i]])))for key in mu.keys():avg_d[key] /= label_count[key]#算两个簇的中点之间的距离cen_d = []for i in range(len(label_set)-1):t = {'c1':label_set[i], 'c2':label_set[i+1], 'dist':np.sqrt(np.sum(np.square(mu[label_set[i]] - mu[label_set[i+1]])))}cen_d.append(t)dbi = 0for k in range(len(label_set)):max_item = 0for i in range(len(label_set)):for j in range(i, len(label_set)):for p in range(len(cen_d)):if cen_d[p]['c1'] == label_set[i] and cen_d[p]['c2'] == label_set[j]:d = (avg_d[label_set[i]] + avg_d[label_set[j]])/cen_d[p]['dist']if d > max_item:max_item = ddbi += max_itemdbi /= len(label_set)return dbi#********* End *********#def calc_DI(feature, pred):'''计算并返回Dunn指数:param feature: 待聚类数据的特征,类型为`ndarray`:param pred: 聚类后数据所对应的簇,类型为`ndarray`:return: Dunn指数'''#********* Begin *********#label_set = np.unique(pred)min_d = []for i in range(len(label_set)-1):t = {'c1': label_set[i], 'c2': label_set[i+1], 'dist': np.inf}min_d.append(t)#计算两个簇之间的最短距离for i in range(len(feature)):for j in range(i, len(feature)):for p in range(len(min_d)):if min_d[p]['c1'] == pred[i] and min_d[p]['c2'] == pred[j]:d = np.sqrt(np.sum(np.square(feature[i] - feature[j])))if d < min_d[p]['dist']:min_d[p]['dist'] = d#计算同一个簇中距离最远的样本对的距离max_diam = 0for i in range(len(feature)):for j in range(i, len(feature)):if pred[i] == pred[j]:d = np.sqrt(np.sum(np.square(feature[i] - feature[j])))if d > max_diam:max_diam = ddi = np.inffor i in range(len(label_set)):for j in range(i, len(label_set)):for p in range(len(min_d)):d = min_d[p]['dist']/max_diamif d < di:di = dreturn d第3关sklearn中的聚类性能评估指标
from sklearn.metrics.cluster import fowlkes_mallows_score, adjusted_rand_scoredef cluster_performance(y_true, y_pred):'''返回Rand指数和FM指数:param y_true:参考模型的簇划分,类型为`ndarray`:param y_pred:聚类模型给出的簇划分,类型为`ndarray`:return: Rand指数,FM指数'''#********* Begin *********#return fowlkes_mallows_score(y_true, y_pred), adjusted_rand_score(y_true, y_pred)#********* End *********#七、机器学习—逻辑回归
第1关逻辑回归核心思想
#encoding=utf8
import numpy as npdef sigmoid(t):'''完成sigmoid函数计算:param t: 负无穷到正无穷的实数:return: 转换后的概率值:可以考虑使用np.exp()函数'''# 使用np.exp()函数计算e的t次方,然后除以1加上e的t次方return 1 / (1 + np.exp(-t))第2关逻辑回归的损失函数
A ACD AB D
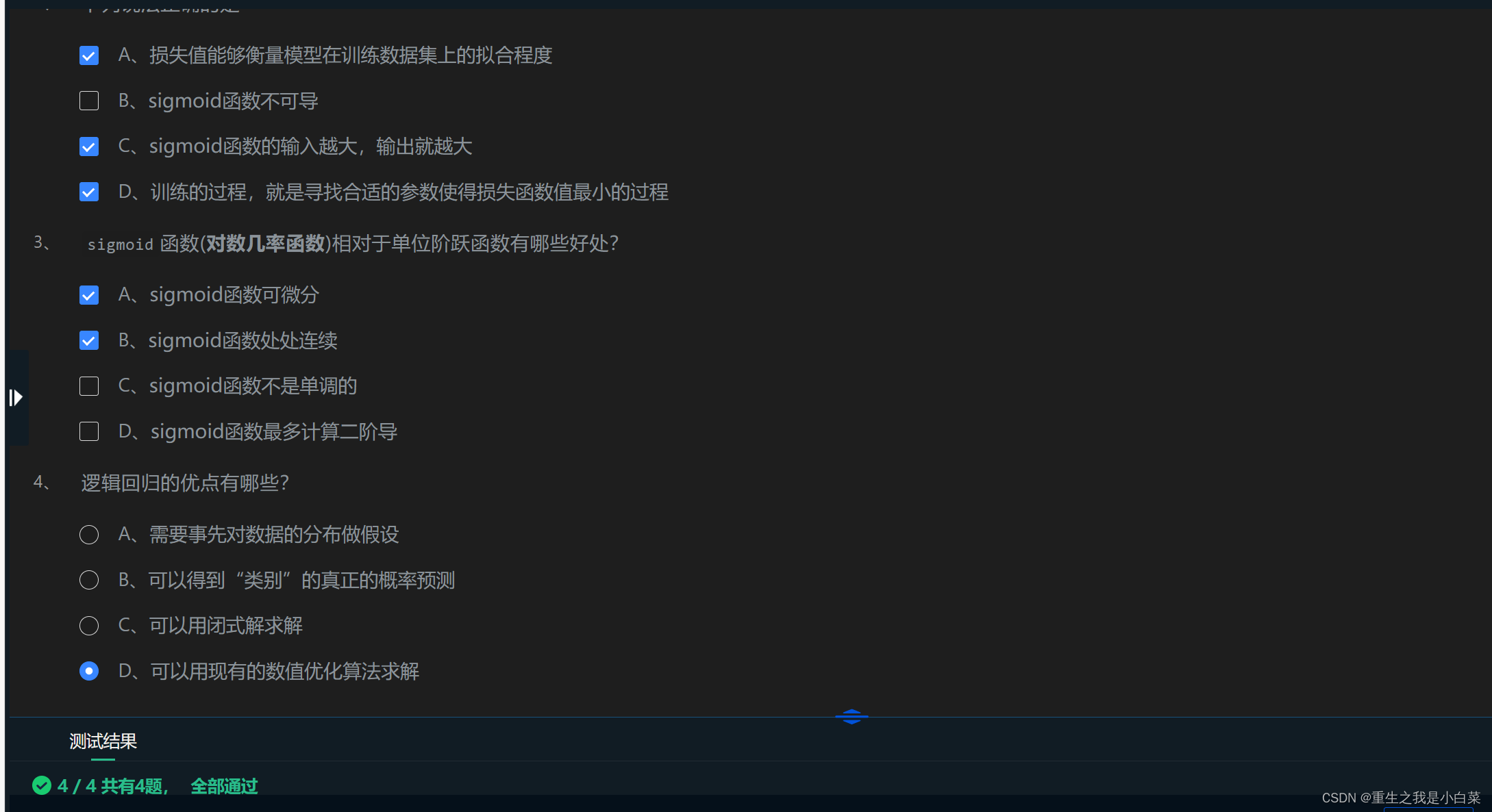
第3关梯度下降
def gradient_descent(initial_theta, eta=0.05, n_iters=1000, epslion=1e-8):'''梯度下降:param initial_theta: 参数初始值,类型为float:param eta: 学习率,类型为float:param n_iters: 训练轮数,类型为int:param epslion: 容忍误差范围,类型为float:return: 训练后得到的参数'''theta = initial_thetai = 0while i < n_iters:i += 1gradient = 2 * (theta - 3)if abs(gradient) < epslion:breaktheta = theta - eta * gradientreturn theta# 调用梯度下降函数
theta = gradient_descent(initial_theta=0)后面的暂时不写
前面四个时必须写的其他等我闲了再写








![[flask]异常抛出和捕获异常](https://img-blog.csdnimg.cn/direct/b52f1ea9c6344737bec4786a080362be.png)